前言
由于视觉伺服与机械臂关系紧密,因此还是从基础开始,把机器人运动学记录一下。
本篇记录刚体的位姿。实际上,空间变换在SLAM专栏里已经讲过一次了,不过机器人学导论给出了更详细的刚体运动说明。
坐标系
通常有两个坐标系,一个是用于参考的世界坐标系(笛卡尔坐标系),一个是以刚体质心为原点的刚体坐标系。
机器人坐标系遵循右手定则,如下图所示
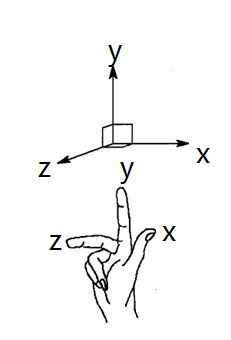
位姿
位姿就是位置与姿态,对应位移与旋转。机器人的位姿必须以世界坐标系作为参照。
位姿表示的是参考系之间的关系。
位置
刚体的位置由矢量表示。
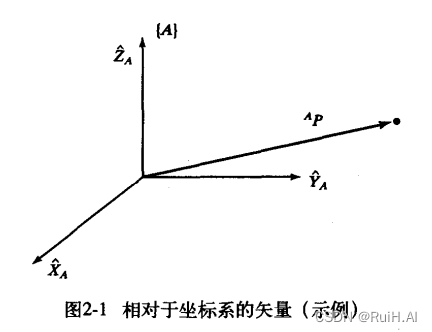
上图中有一个点
P
P
P,以坐标系
{
A
}
\{A\}
{A}为参考,就可以将矢量
O
P
OP
OP来表示
A
P
^AP
AP的位置,其左上标表示参考系。
A
P
^AP
AP的坐标表示为:
A
P
=
[
p
x
,
p
y
,
p
z
]
T
^AP = [p_x,p_y,p_z]^T
AP=[px?,py?,pz?]T
姿态
刚体的姿态由刚体坐标系在参考系中三个主轴的单位矢量表示。
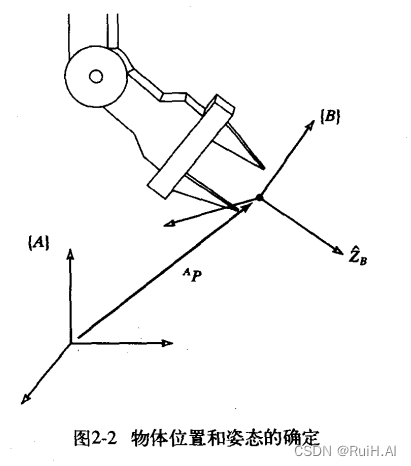
上图中,
X
^
B
,
Y
^
B
,
Z
^
B
\hat X_B,\hat Y_B, \hat Z_B
X^B?,Y^B?,Z^B?表示右上角刚体的三个主轴方向的单位矢量,它们在参考系
{
A
}
\{A\}
{A}中的表示为
A
X
^
B
,
A
Y
^
B
,
A
Z
^
B
^A\hat X_B, ^A\hat Y_B, ^A\hat Z_B
AX^B?,AY^B?,AZ^B?。这三个单位矢量就组成了旋转矩阵:
B
A
R
=
(
A
X
^
B
A
Y
^
B
A
Z
^
B
)
^A_BR=(^A\hat X_B \quad ^A\hat Y_B \quad ^A\hat Z_B)
BA?R=(AX^B?AY^B?AZ^B?)
那么如何计算刚体的主轴单位矢量在参考系中的坐标呢?
以
A
X
^
B
^A\hat X_B
AX^B?为例,其x坐标的值实际上就是
A
X
^
B
^A\hat X_B
AX^B?在参考系的X轴上的投影,y, z坐标就是在参考系的Y, Z轴上的投影:
B
A
R
=
(
A
X
^
B
A
Y
^
B
A
Z
^
B
)
=
[
X
^
B
?
X
^
A
Y
^
B
?
X
^
A
Z
^
B
?
X
^
A
X
^
B
?
Y
^
A
Y
^
B
?
Y
^
A
Z
^
B
?
Y
^
A
X
^
B
?
Z
^
A
Y
^
B
?
Y
^
A
Z
^
B
?
X
^
A
]
^A_BR=(^A\hat X_B \quad ^A\hat Y_B \quad ^A\hat Z_B) = \begin{bmatrix} \hat X_B \cdot \hat X_A & \hat Y_B \cdot \hat X_A & \hat Z_B \cdot \hat X_A\\ \hat X_B \cdot \hat Y_A & \hat Y_B \cdot \hat Y_A & \hat Z_B \cdot \hat Y_A\\ \hat X_B \cdot \hat Z_A & \hat Y_B \cdot \hat Y_A & \hat Z_B \cdot \hat X_A\\ \end{bmatrix}
BA?R=(AX^B?AY^B?AZ^B?)=???X^B??X^A?X^B??Y^A?X^B??Z^A??Y^B??X^A?Y^B??Y^A?Y^B??Y^A??Z^B??X^A?Z^B??Y^A?Z^B??X^A?????
旋转矩阵是个正交矩阵,证明也很简单:
B
A
R
T
?
B
A
R
=
[
A
X
^
B
T
A
Y
^
B
T
A
Z
^
B
T
]
(
A
X
^
B
A
Y
^
B
A
Z
^
B
)
=
I
3
^A_BR^T\ ^A_B R= \begin{bmatrix} ^A\hat X^T_B \\ ^A\hat Y^T_B \\ ^A\hat Z^T_B \end{bmatrix} (^A\hat X_B \quad ^A\hat Y_B \quad ^A\hat Z_B) = I_3
BA?RT?BA?R=???AX^BT?AY^BT?AZ^BT?????(AX^B?AY^B?AZ^B?)=I3?
同方向的单位矢量的内积为1,相互垂直的单位矢量内积为0,因此
A
X
^
B
T
?
A
X
^
B
=
1
,
A
X
^
B
T
?
A
Y
^
B
=
0
^A\hat X^T_B \ ^A\hat X_B=1, ^A\hat X^T_B \ ^A\hat Y_B=0
AX^BT??AX^B?=1,AX^BT??AY^B?=0,所以能得到上面的单位矩阵。
位姿变换
位姿变换指刚体坐标系的位置和姿态发生变化,即平移和旋转,得到刚体系与参考系之间的相对位姿
仍然以图2-2为例,刚体坐标系相对于参考系的位姿变换可表示为:
{
B
A
R
,
?
A
P
B
O
R
G
}
\{^A_B R, \ ^AP_{BORG} \}
{BA?R,?APBORG?}
也就是SLAM十四讲中的
R
,
t
R,t
R,t
映射
映射表示的是同一点在不同坐标系之间的坐标转换。
映射包括平移和旋转。
平移
平移与刚体坐标系原点的位置相关。
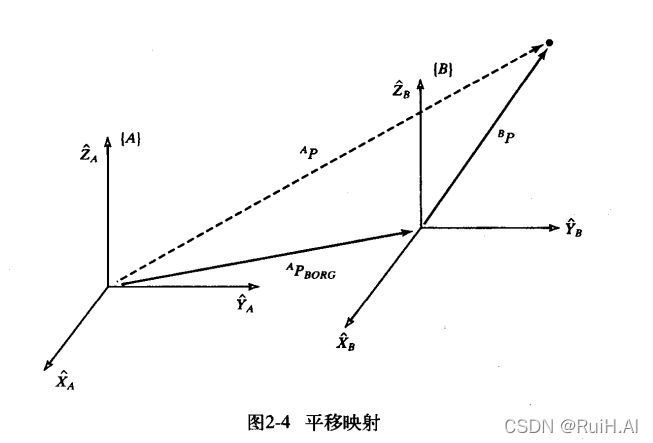
上图中,已知
B
P
^BP
BP表示点P在坐标系
{
B
}
\{B\}
{B}中的位置,
A
P
B
O
R
G
^AP_{BORG}
APBORG?表示在参考系
{
A
}
\{A\}
{A}下
{
B
}
\{B\}
{B}原点的位置。则
A
P
^AP
AP可表示为:
A
P
=
?
B
P
+
?
A
P
B
O
R
G
^AP= \ ^BP + \ ^AP_{BORG}
AP=?BP+?APBORG?
只有在两个坐标系的姿态相同时,才能进行上面的平移。
旋转
旋转与刚体坐标系的姿态相关。
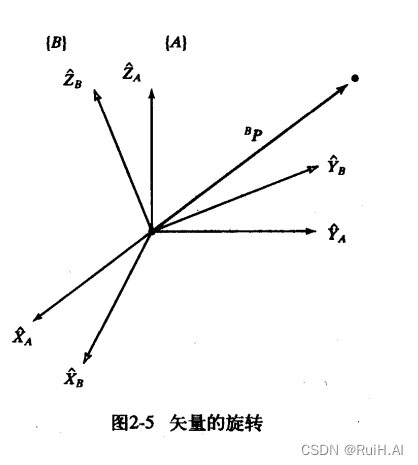
上图中,已知
B
P
^BP
BP表示点P在坐标系
{
B
}
\{B\}
{B}中的位置。
A
P
^AP
AP表示在参考系
{
A
}
\{A\}
{A}下的位置,即矢量
A
P
^AP
AP在参考系主轴方向
X
^
A
,
Y
^
A
,
Z
^
A
\hat X_A, \hat Y_A, \hat Z_A
X^A?,Y^A?,Z^A?的投影(单位矢量内积)。此外,我们知道,向量内积需要在同一坐标系下表示才有意义。则
A
P
^AP
AP可表示为:
A
P
=
[
B
X
^
A
?
?
B
P
B
Y
^
A
?
?
B
P
B
Z
^
A
?
?
B
P
]
=
?
B
A
R
?
B
P
^AP= \begin{bmatrix} ^B \hat X_A \cdot\ ^BP & ^B \hat Y_A \cdot\ ^BP & ^B \hat Z_A \cdot\ ^BP \end{bmatrix} = \ ^A_BR \ ^BP
AP=[BX^A???BP?BY^A???BP?BZ^A???BP?]=?BA?R?BP
变换
变换=先旋转,后平移。
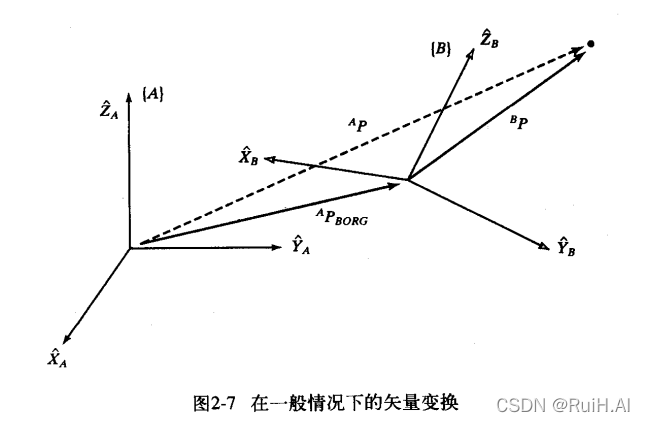
上图中,需要使用
B
P
^BP
BP表示
A
P
^AP
AP。首先将
B
P
^BP
BP映射到一个中间坐标系
{
B
′
}
\{B'\}
{B′},该坐标系姿态与
{
A
}
\{A\}
{A}相同,原点与
{
B
}
\{B\}
{B}相同。然后再用
B
′
P
^{B'}P
B′P表示
A
P
^AP
AP:
A
P
=
?
B
′
P
+
?
A
P
B
′
O
R
G
=
?
B
B
′
R
?
B
P
+
?
A
P
B
′
O
R
G
=
?
B
A
R
?
B
P
+
?
A
P
B
O
R
G
^AP = \ ^{B'}P + \ ^AP_{B'ORG} = \ ^{B'}_BR \ ^BP + \ ^AP_{B'ORG} = \ ^{A}_BR \ ^BP + \ ^AP_{BORG}
AP=?B′P+?APB′ORG?=?BB′?R?BP+?APB′ORG?=?BA?R?BP+?APBORG?
也就对应SLAM十四讲中的
P
′
=
R
P
+
t
P'=RP+t
P′=RP+t
引入齐次矩阵,就有了变换矩阵的概念:
[
A
P
1
]
=
[
?
B
A
R
A
P
B
O
R
G
0
1
]
[
?
B
P
1
]
A
P
=
?
B
A
T
?
B
P
\begin{bmatrix} ^AP \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \ ^A_BR & ^AP_{BORG} \\ {\bf 0} & 1 \\ \end{bmatrix} \begin{bmatrix} \ ^BP \\ 1 \\ \end{bmatrix} \\ \quad \\ \\ \quad \\ ^AP = \ ^A_BT \ ^BP
[AP1?]=[?BA?R0?APBORG?1?][?BP1?]AP=?BA?T?BP
复合变换
如果已知
B
A
T
,
?
C
B
T
^A_B T, \ ^B_CT
BA?T,?CB?T,则可以通过
C
P
^CP
CP表示
A
P
^AP
AP:
A
P
=
B
A
T
?
C
B
T
?
C
P
^AP = ^A_BT \ ^B_CT \ ^CP
AP=BA?T?CB?T?CP
逆变换
旋转矩阵的逆:
B
A
R
=
?
A
B
R
T
^A_B R = \ ^B_AR^T
BA?R=?AB?RT
变换矩阵的逆:
[
?
B
A
R
T
?
B
A
R
T
?
A
P
B
O
R
G
0
1
]
\begin{bmatrix} \ ^A_BR^T & -^A_BR^T\ ^AP_{BORG} \\ {\bf 0} & 1 \\ \end{bmatrix}
[?BA?RT0??BA?RT?APBORG?1?]
变换矩阵的逆有两种求法,一种是直接根据矩阵求逆;另一种是通过变换性质求逆。介绍一下后一种。

如果已知
A
P
^AP
AP求
B
P
^BP
BP,有:
B
P
=
?
A
B
R
?
A
P
+
?
B
P
A
O
R
G
^BP = \ ^B_AR \ ^AP + \ ^BP_{AORG}
BP=?AB?R?AP+?BPAORG?
如果
A
P
^AP
AP是
{
B
}
\{B\}
{B}的原点,即:
0
=
B
P
B
O
R
G
=
A
B
R
?
A
P
B
O
R
G
+
?
B
P
A
O
R
G
?
B
P
A
O
R
G
=
?
A
B
R
?
A
P
B
O
R
G
=
?
B
A
R
T
?
A
P
B
O
R
G
?
B
P
=
?
B
A
R
T
?
A
P
?
?
B
A
R
T
?
A
P
B
O
R
G
{\bf 0} = ^BP_{BORG} = ^B_AR \ ^AP_{BORG} + \ ^BP_{AORG} \\ \quad \\ \ ^BP_{AORG} = - ^B_AR \ ^AP_{BORG} = -^A_BR^T \ ^AP_{BORG} \\ \quad \\ \ ^BP = \ ^A_BR^T \ ^AP - \ ^A_BR^T \ ^AP_{BORG}
0=BPBORG?=AB?R?APBORG?+?BPAORG??BPAORG?=?AB?R?APBORG?=?BA?RT?APBORG??BP=?BA?RT?AP??BA?RT?APBORG?
旋转矩阵,变换矩阵的意义
旋转矩阵的意义
- 描述一个坐标系相对参考坐标系的姿态
- 将点从一个坐标系转换到参考坐标系
- 将向量在一个坐标系中进行旋转
变换矩阵的意义
- 描述一个坐标系相对参考坐标系的位姿
- 将点从一个坐标系转换到参考坐标系
- 将向量在一个坐标系中先旋转,后平移
后记
本篇实际上是SLAM十四讲中位姿变换的更清晰的表述方法,参考系放左上标。