[人工智能]从零实现深度学习框架——神经网络入门

引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不使用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。
本系列文章首发于微信公众号：JavaNLP

我们上篇文章了解了神经元的概念，本文来学习一下神经网络(Neural Network)的基本知识。

异或问题

我们先来看下著名的异或问题，该问题曾导致了神经网络研究的十年低谷。

本文以下图片来自nlp3

异或问题(XOR problem)：输入两个布尔数值(0或1)，当两个数值不同时输出为1，否则输出为0。

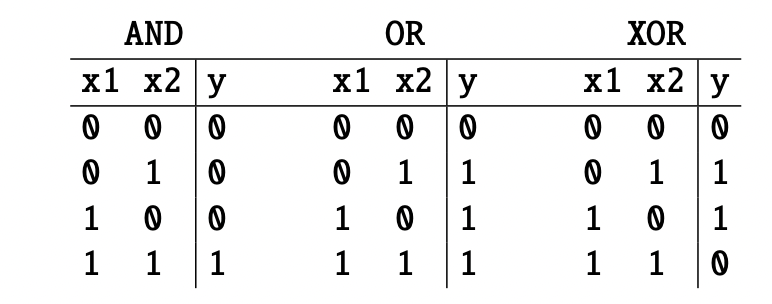
如上图，假设输入是x1、x2，输出是y。

在介绍神经网络之前，我们先来了解一下感知机(perceptron)，感知机可以类比成一个神经元，但是它没有一个非线性激活函数。

感知机是一种二元分类器(具有权重$w$和偏置$b$)，把输入$x$(实数值向量)映射到二元的输出上。输出可以记为0或1，或者说是-1和+1。感知机的计算方法如下：
$$y=\{\begin{array}{ll}0,& \text{if?w?x+b≤0?}\\ 1,& \text{if?w?x+b>0?}\end{array}\text{\hspace{1em}(1)}$$
我们可以很容易构建出能计算与运算(AND)和或运算(OR)的感知机：

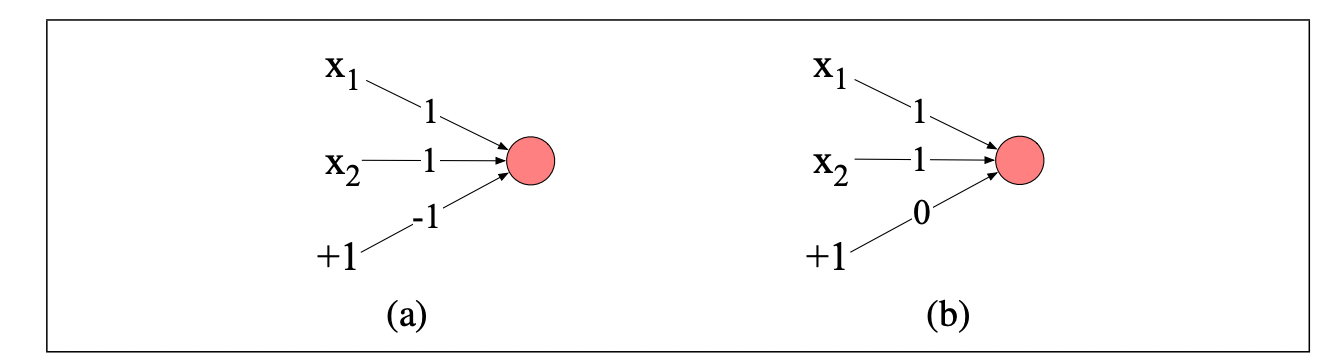
上图是实现与(a)和或(b)运算的感知机。输入分别是$x_1,x_2$?。上图连线上的数值代表权重或偏置。

比如(a)为$x_1+x_2?1$，输入为$1,1$时，结果为$1>0$，所以输出$y=1$。

除了与运算(AND) 和 或运算(OR)，异或运算也很重要。

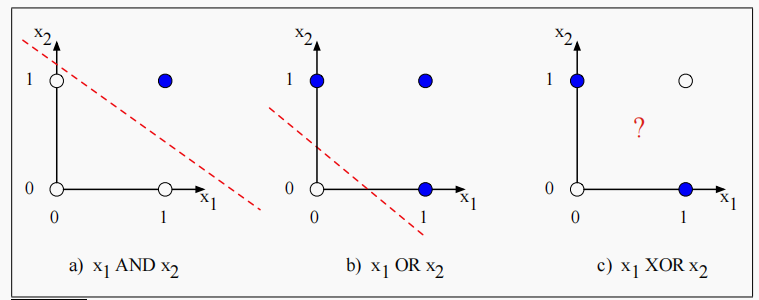
但是我们不可能通过一个感知机来实现异或运算。因为感知机是一个线性分类器，对于二维输入$x_1$和$x_2$，感知机方程$w_1{x}_1+w_2{x}_2+b=0$是一个直线的方程，该直线作为二维空间中的决策边界，其中一侧代表输出为$0$，另一侧代表输出为$1$。

下图显示了可能的逻辑输入（00、01、10和11），以及由AND和OR分类器的一组可能的参数绘制的线。但我们没有办法画出一条之线将XOR的正例（01和10）与负例（00和11）区分开来。我们说XOR不是一个线性可分的函数。

解决方案：神经网络

尽管异或函数无法被单个感知机表示，但可以被基于感知机单元的分层网络表示。我们看如何使用两层ReLU单元计算异或问题。

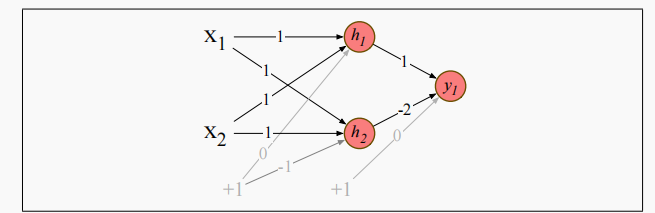
该两层网络中有三个ReLU单元，分别是$h_1,h_2$和$y_1$。有向边上的数字代表每个单元的权重$w$，灰色有向边代表偏置。

假设输入$x=[0,0]$，我们计算

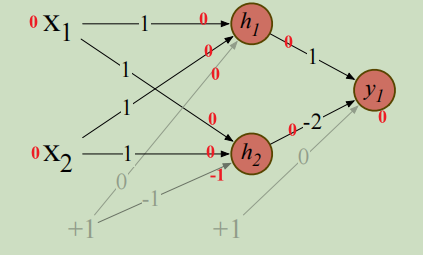
这里用到了ReLU激活函数，所以$h_2$的输出是$0$，对于其他的输入可以自己验证一下。

本例中我们固定的权重值，但实际上神经网络的权重是通过反向传播算法自动学习的。

下面我就来了解下最常见的神经网络。

前馈神经网络

前馈神经网络( Feedforward Neural Networks,FNN)是一个逐层传播的没有循环的多层网络。由于历史原因，多层前馈网络，也被称为多层感知机(multi-layer perceptron,MLP)。但这是一个技术误称，因为现代多层网络中的神经元不是感知机(感知机是纯线性的，但现代网络中的神经元带有非线性激活函数)。

简单(两层)前馈网络有三种节点：输入单元、隐藏单元和输出单元，如下图所示。

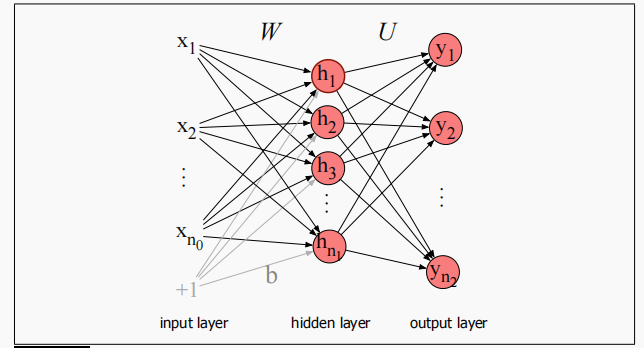
输入层$x$通常代表由多个标量组成的一个向量；神经网络的核心是隐藏层$h$，由隐藏单元$h_i$组成，每个隐藏单元都是我们前面了解的神经元，隐藏层对其输入计算加权和并应用一个非线性函数。在标准架构中，每层都是全连接的(每个神经元都连接了每个输入)。

为什么说这是一个两层神经网络，因为我们在描述层数的时候，通常忽略掉输入层。

注意每个隐藏单元都有一个权重参数和一个偏置。我们通过将每个单元$i$的权重向量和偏差组合成整个层的权重矩阵$W$和偏置向量$B$来表示整个隐藏层的参数。权重矩阵$W$中的每个元素$W_{ji}$表示从第$i$个输入单元$x_i$到第$j$个隐藏单元$h_j$的连接的权重。

使用一个矩阵$W$表示整个层的权重的优点是，现在通过简单的矩阵操作，可以非常有效地完成前馈网络的隐层计算。实际上，计算只有三个步骤：将权值矩阵乘以输入向量$x$，加上偏置向量$b$，再应用激活函数$g$(比如Sigmoid、tanh或ReLU等)。

隐藏层的输出，向量$h$，因此可以如下计算(这里假设使用Sigmoid作为激活函数)：
$$h=\sigma (Wx+b)\text{\hspace{1em}(2)}$$

有时，我们也用$\sigma$泛指任意激活函数，而不仅代表Sigmoid。

$Wx+b$的结果是一个向量，因此$\sigma$应用到该向量上。

下面我们介绍一些常用的记号，以更好的描述后面的内容。

在本例中，我们称输入层为网络的第$0$层(layer 0)，$n_0$表示输入层的输入个数，所以$x$是维度为$n_0$的实数向量，或正式一点说$x\in {\mathbb{R}}^{n_0}$的列向量$[n_0\times 1]$；我们称隐藏层为第$1$层(layer 1)，输出层为第$2$层(layer 2)；隐藏层的维度(隐藏层中单元个数)是$n_1$，所以$h\in {\mathbb{R}}^{n_1}$，同时$b\in {\mathbb{R}}^{n_1}$(因为每个隐藏单元都有一个偏置)；然后权重矩阵$W$的维度是$W\in {\mathbb{R}}^{n_1\times n_0}$(结合公式$(2)$)。

因此公式$(2)$中的某个输出$h_j$，可以表示为$h_j=\sigma ({\sum }_{i=0}^{n_0}{W}_{ji}{x}_i+b_j)$。

经过隐藏层，我们将维度为$n_0$的输入向量表示成了维度为$n_1$的隐藏向量，然后传递给输出层计算最终的输出。输出的维度取决于实际的问题，比如回归问题则为一个实数值(只有一个输出)。但常见的是分类问题。若是二分类，那么输出层的维度就是$2$，即输出单元(输出节点)只有两个；若是多分类，那么输出单元则有多个。

我们来看下输出层发生了什么，输出层也有一个权重矩阵($U$)，(除了输入层没有权重，这也是为什么输入层没有计算层数的原因之一)，但有些模型输出层是没有偏置$b$的，所以权重矩阵$U$直接与其输入向量$h$相乘得到中间输出$z$:
$$z=Uh\text{\hspace{1em}(3)}$$
输出层有$n_2$个输出节点，所以$z\in {\mathbb{R}}^{n_2}$，权重矩阵$U\in {\mathbb{R}}^{n_2\times n_1}$，其中$U_{ij}$是从隐藏层中第$j$个单元到输出层第$i$个单元的权重。

注意，这里的$z$是一个实数向量，通常不是最终的输出，对于分类模型中，我们需要将其转换为一个概率分布。

有一个很方便的函数可以将实数向量归一化(normalizing)为概率分布，该函数就是Softmax。假设给定维度为$d$的向量$z$，Softmax定义为：
$$\text{softmax}(z_i)=\frac{\exp (z_i)}{{\sum }_{j=1}^d\exp (z_j)}1\le i\le d\text{\hspace{1em}(4)}$$
即我们可以把一个具有一个隐藏层的神经网络分类器看作是构建一个向量$h$，它是输入的一个向量表示，然后对网络中的$h$中运行标准的多元逻辑回归。相比之下，逻辑回归中的特征主要是通过特征模板手工设计的。所以神经网络就像Softmax逻辑回归，但是优点为：(a)可以有更多的层，因为深度神经网络就像一层又一层的逻辑回归分类器；(b)中间层有许多可选的激活函数(tanh，ReLU，sigmoid)而不只是sigmoid（尽管我们可能使用$\sigma$来表示任何激活函数）；?不是通过特征模板形成特征，网络前面的层自己形成特征表示。

我们就可以得到本例中的两层前馈网络，又称为单隐藏层前馈网络，的最终表示：
$$\begin{array}{rl}h& =\sigma (Wx+b)\\ z& =Uh\\ y& =\text{softmax}(z)\end{array}\text{\hspace{1em}(5)}$$
其中$x\in {\mathbb{R}}^{n_0},h\in {\mathbb{R}}^{n_1},b\in {\mathbb{R}}^{n_1},W\in {\mathbb{R}}^{n_1\times n_0},U\in {\mathbb{R}}^{n_2\times n_1}$，然后输出向量$y\in {\mathbb{R}}^{n_2}$。我们称该网络为两层神经网络。所以，这么说的话，逻辑回归是一层网络。在资源能支撑的情况下，我们可以自由加深前馈网络的层数，这样可以得到真正的深层神经网络。

更常见的记号表示

下面我们介绍一些更常见的记号，Andrew Ng也用的这套表示方法。具体来说，使用方括号中的上标来表示层数，从输入层的0开始。

因此，$W^{[1]}$表示(第一个)隐藏层的权重矩阵，$b^{[1]}$表示(第一个)隐藏层的偏置向量；$n_j$将表示第$j$层的单元数；$g(?)$来代表激活函数，中间层往往用ReLU或tanh激活函数，输出层往往是softmax；$a^{[i]}$来表示第$i$层的输出，$z^{[i]}$表示$W^{[i]}{a}^{[i?1]}+b^{[i]}$；第0层是输入层，所以我们将更一般地将输入$x$称为$a^{[0]}$。

这样我们重新表示上面的单隐藏层前馈网络为：
$$\begin{array}{rl}{z}^{[1]}& =W^{[1]}{a}^{[0]}+b^{[1]}\\ a^{[1]}& =g^{[1]}(z^{[1]})\\ z^{[2]}& =W^{[2]}{a}^{[1]}+b^{[2]}\\ a^{[2]}& =g^{[2]}(z^{[2]})\\ \hat{y}& =a^{[2]}\end{array}\text{\hspace{1em}(6)}$$

替换偏置单元记号

为了简化网络的描述，我们可以省略显示地描述偏置$b$。为此，我们向每个层添加一个虚拟节点$a_0$，其值将始终为$1$。因此，输入层$0$层将具有虚拟节点$a_0^{[0]}=1$，层$1$将具有$a_0^{[1]}=1$，以此类推。这个虚拟节点仍然具有一个关联的权重，该权重表示偏差值$b$，比如将下面的等式：
$$h=\sigma (Wx+b)$$
替换为：
$$h=\sigma (Wx)\text{\hspace{1em}(7)}$$
但是现在$x$向量不是$n_0$个值，变成了$n_0+1$个值，包括固定的值$x_0=1$，这样变成了$x=x_0,?,x_{n_0}$。我们就可以更改计算$h_j$的方式，从：
$$h_j=\sigma \left(\sum _{i=1}^{n_0}{W}_{ji}{x}_i+b_j\right)\text{\hspace{1em}(8)}$$
变成了：
$$h_j=\sigma \left(\sum _{i=0}^{n_0}{W}_{ji}{x}_i\right)\text{\hspace{1em}(9)}$$
其中用$W_{j0}$替换了$b_j$，我们画图时也可以进行简化：

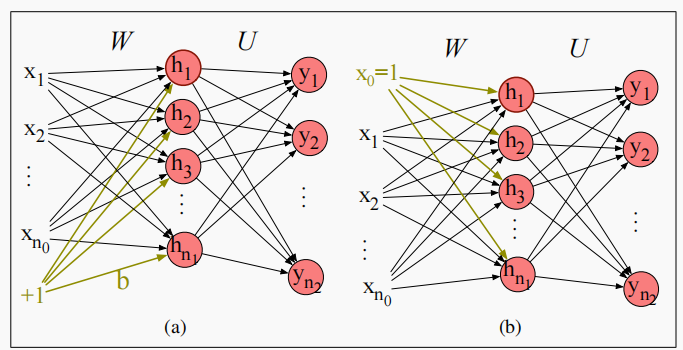
从上图左边$(a)$简化为右边的$(b)$。

References

1. Speech and Language Processing