[人工智能]欧拉函数：求小于等于n且与n互质的数的个数

求小于等于n且与n互质的数的个数

互质穷举法

1. 互质：两个数互质代表两者最大公约数为1
2. 最大公约数求法：辗转相除法，最小公倍数：较大值除以最大公约数乘以较小值
3. 辗转相除法：
   1. 较大的数a取模较小的数b，得取模值c
   2. 若取模值等于0 则最大公约数为取模值，否则继续下一步
   3. a与c再次取模，回到第二步

   //求最大公约数gcd以及最大公倍数lcm
    // 36 24 36/24
    // 24 12 24/12
    // 0 结束最大公约数为12
    // 求最小公倍数
    // lcm(a, b) = (a * b)/gcd(a, b)
    public static int gcd(int a, int b){
        //a>=b
        //辗转相除法
        if (b==0){
            return a;
        }
        return gcd(b,a%b);
    }
   

4. 穷举到n，一一判断该数与n的最大公约数是否为1，即是否为互质

结论：可以实现，但时间复杂度太高

采取欧拉函数进行求取

在数论，对正整数n，欧拉函数是小于等于n的正整数中与n互质的数的数目.

n为正整数n，p1、p----2 ……pn 为正整数n的质因数

n的质因数：既是n的因数，又是质数的数

计算方法：
$$?(n)=n\times (\frac{p_1?1}{p_1})\times (\frac{p_2?1}{p_2})?\times (\frac{p_n?1}{p_n})$$
例：
$$?(10)=10\times \frac{1}{2}\times \frac{4}{5}=4$$

1. 质数的求法：因数只有1和其本身

   1. 单个质数n的判断

      依次判断2到 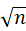的数被n取模的值是否等于零，存在任意一个即不为质数

      当p大于 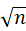时，代表数p一定可以得到一个小于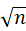的数和一个大于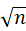的成对因数，不为质数

   2. 从2到n的质数的判断

      非穷举，穷举时间复杂度为O(n)，使用素数筛法为O()

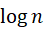      为保证效率，质数为false，合数为true

      1. 标记2到n的数都为质数，为false，布尔数组默认值为false，无需再一一标记

      2. 从2开始标记数，找到第一个为false的数p

      3. 标记数p的倍数为合数，即为true，倍数标记从p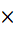p 开始，直至数p等于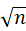，结束标记

         原因：

         p的倍数的因数必有p，不符合质数条件，每次从 p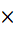p 开始标记是由于p-1的部分已经进行了标记，不再重复标记，

?

4. 使得下一个数p 为未被标记为合数的数，即数值仍为333333false的数，重复第三步

5. 将标记为false 的，即为质数的全部输出

2. 采取素数筛法求取质数时，可将倍数标记的操作修改为乘以(1-1/p)，使得每一个数都能乘以其质因数

3. 依次存入数组中，最后统一依次输出结果。

public static int f1(int n){
        int res = n;
        for (int i = 2;i*i<=n;i++){
            if (n % i==0){
                res = res / i*(i-1);//res/i
                while (n % i == 0){
                    n/=i;
                }
            }
        }
        if (n>1){
            res = res/n*(n-1);
        }
        return res;
    }
    //区间内欧拉函数取值
    public static int[] f2(int n){
        int[] count = new int[n+1];
        for (int i = 1;i <= n;i++){
            count[i]=i;
        }
        for (int i =2 ;i <= n;i++){
            if (count[i] == i){
                for (int j = i;j <= n;j+=i){
                    count[j] = count[j]/i*(i-1);
                }
            }
        }
        return count;
    }

知识点：

1. 最大公约数、最小公倍数

2. 单一质数判断

3. 质数筛法：埃氏筛法

4. 欧拉函数