推荐链接:
梯度下降优化器可视化?RMSprop - 搜索结果 - 知乎
pytorch相关api?torch.optim.Adam算法里面参数的含义_子燕若水的博客-CSDN博客_adam中的weight_decay
正文内容:
原始梯度下降算法
delta = - learning_rate * gradient
theta += delta
导致的问题是特别陡峭的地方和特别平缓的地方采用同样的learning_rate,如果learning_rate太大很容易在陡峭的地方一个大幅度的迭代会跨过最优解很远,如果learning_rate太小,在平缓的地方会学习很慢。
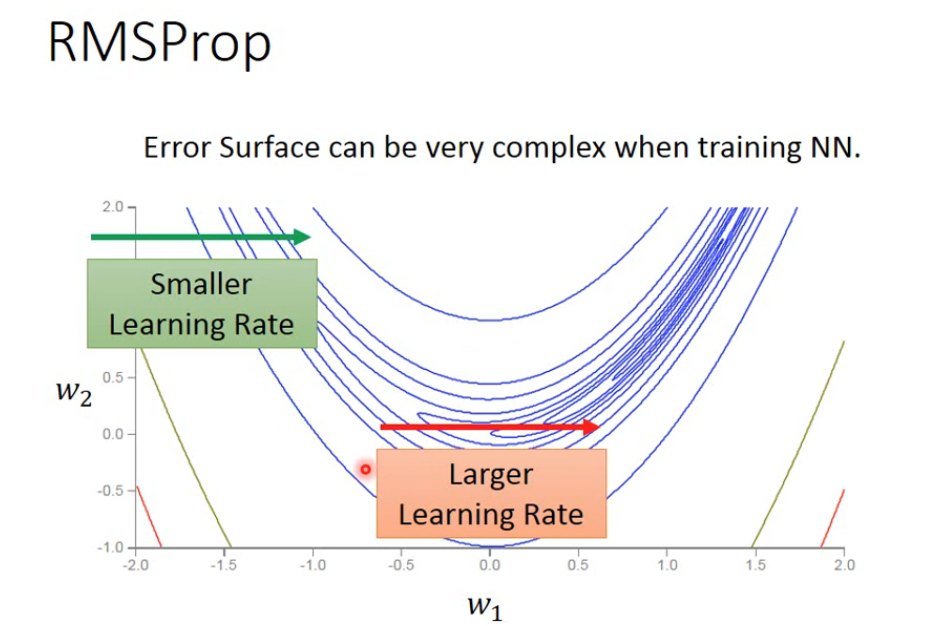
所以有了RMSProp版的优化器,
sum_of_gradient_squared = previous_sum_of_gradient_squared * decay_rate+ gradient2 * (1- decay_rate)
delta = -learning_rate * gradient / sqrt(sum_of_gradient_squared)
theta += delta

RMSProp的优点就是学习率?要除以一个?
,而?
的主要成分就是当前梯度的模的大小,即当前坡度的陡峭程度,?这样就可以使得当前坡度越陡峭,迈出的步伐越小,如果当前坡度越平缓,迈出的步伐越大。
当然还有一个次要部分,就是上一次迭代中
的模的大小,这个值纪录了最近经历的坡度的历史陡峭程度,是一个context值,可以一定程度上推测未来几个迭代中坡度的大概情况。
上面只考虑了历史的梯度,如果考虑历史成分从历史梯度变成前一次的移动方向及大小则称之为动量法(momentum)。
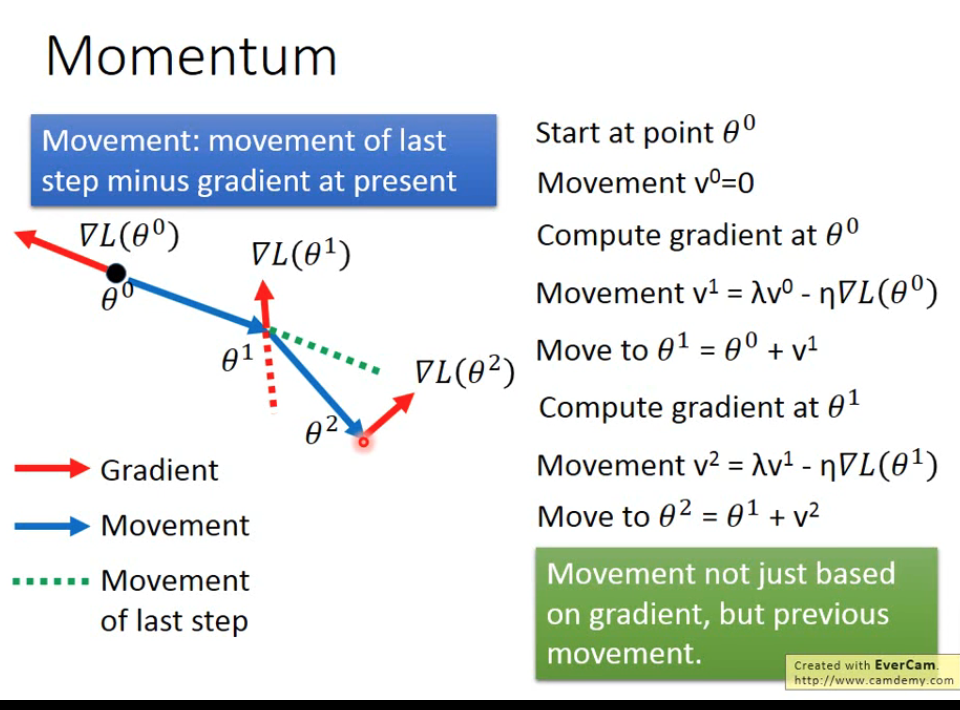
?仔细看v的变化过程,其实仅仅考虑前一次的移动方向(及大小)就是考虑了历史所有移动方向(及大小)。
如果既考虑历史的梯度,同时也考虑历史的移动方向,则有Adam优化法:
