[人工智能] 强化学习基础

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 强化学习基础 -> 正文阅读

[人工智能]强化学习基础

定义

强化学习（Reinforcement Learning，RL）是智能体（Agent）为了最大化长期回报（Return）的期望，通过观察系统环境，不断试错（Trial-and-Error）进行学习的过程。
从强化学习的定义可以看出，强化学习具有两个最主要的特征：

通过不断试错来学习；
追求长期回报的最大化。

强化学习的框架一般包含5个构成要素，包括：

环境（Environment）；
智能体（Agent）；
观察（Observation）；
行动（Action）；
奖励（Reward）。

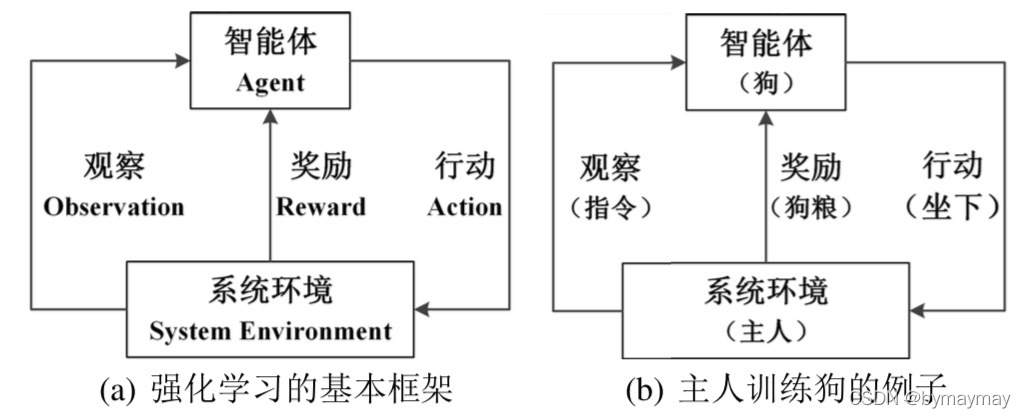
强化学习的基本框架如下图 (a) 所示，智能体对系统环境进行观察后产生行动，从系统环境中获得相应的奖励，智能体观察系统对自己上一次行动的奖励信号后，重新调整自己的下一次的行动策略。下图 (b) 展示了主人训练狗的过程就是强化学习过程的一个简单例子。主人想训练狗听从自己的指令，如果狗听从指令，产生了正确的行动，则主人会喂狗粮；如果狗未听从指令，产生了错误的行动，则狗得不到狗粮。在这个强化学习的例子中，主人充当着系统环境的角色，狗是智能体。狗（智能体）通过对主人（系统环境）的指令观察，产生相应的行动，狗粮就是主人对狗行动的奖励。
?
在这里插入图片描述

完全观测与不完全观测

上述框架是站在上帝视角描述问题，而强化学习的概念默认是站在智能体的角度看问题。

在 $t$ 时刻，系统环境的实际状态记为 $S^e_t$ ，智能体观测到的系统状态记为 $S^a_t$ 。智能体对系统状态的观测可以分为两种情况：

完全观测（Full Observability）；
不完全观测（Partial Observability）。

完全观测 $O_t$ 指的是智能体观测到的状态 $S^a_t$ 就是系统真实的全局状态 $S^e_t$ ，即完全观测 $O_t=S^a_t=S^e_t$ 。
不完全观测 $\tilde{O}_t$ 指的是智能体只能观测到系统的局部状态，即不完全观测 $\tilde{O}=S^a_t\neq S^e_t$ 。

在接下来的内容中，除非特别说明，智能体对系统环境的观察都属于完全观测。
在完全观测的情况下，将智能体观察到的状态 $S^a_t$ 和系统真实的全局状态 $S^e_t$ 统一简称为状态（State）。

在 $t$ 时刻，智能体观测到系统环境的状态 $S_t$ ，并产生相应的行动 $A_t$ ，系统会在一下个时刻 $t + 1$ 给出奖励 $R_{t+1}$ ，并进入新状态 $S_{t+1}$ 。针对行动 $A_t$ ，系统给出的奖励记为 $R_{t+1}$ 。在强化学习过程中，智能体与系统环境产生的交互形成了相应的历史记录。历史记录是由一系列的状态、行动和奖励组成的序列： $\{S_1,A_1,R_2,\cdots,S_{t-1},A_{t-1},R_t,\cdots\}$ 。

针对行动 $A_t$ ，系统发出的奖励是 $R_{t+1}$ ，而不是 $R_{t}$ ，这只是一种针对时间序列的约定，目前大部分强化学习资料都采用这种约定。如果采用以下约定，针对行动 $A_t$ ，系统给出的奖励是 $R_{t}$ ，也是可以的，只需要在上下文环境中保持一致就行。为了与现有资料保持一致，在本书中约定，在 $t$ 时刻，智能体观察到系统状态 $S_t$ ，智能体根据自身的策略采取相应的行动 $A_t$ ，系统针对该行动给出奖励 $R_{t+1}$ ，与此同时，系统进入到下一个状态 $S_{t+1}$ 。

基本概念

折现因子

在强化学习过程中，智能体的目标不是最大化即时奖励，而是最大化长期回报。也就是说，智能体目光长远地更关心行动产生的长期回报。
针对 $t$ 时刻的状态 $S_{t}$ 和行动 $A_{t}$ ，系统产生的奖励是 $R_{t+1}$ 。长期回报是未来奖励在当前时刻的累计值，那么由 $t$ 时刻的状态和行动产生的长期回报是 $G_t=R_{t+1}+R_{t+2}+R_{t+3}+\cdots$ 吗？

答案是不一定。为什么呢？
因为这里涉及一个经济学的概念：折现（Discounting）。

我们先来看一个例子。
假设小明现在有 $x$ 元，小明存一年期定期，存 $1$ 年后的钱为 $10$ 万元，那么有以下公式成立： $x(1+3\%)=100000$ ，解得 $x = 97087$ 。当前小明只需要去银行存 9.7087 万元，一年后就能有 10 万元的购车款。也就是说一年后的 10 万元和现在的 9.7087 万元是等价的。在这个例子里，把 1 年后的钱换算到现在，需要乘以折现因子 $\gamma =0.97087$ 。

强化学习过程将未来的奖励计入目前的回报时，需要将未来的奖励乘以折现因子（Discount Factor），记为 $\gamma$ 。
?
在这里插入图片描述

强化学习过程将未来的奖励计入目前的回报时，需要将未来的奖励乘以折现因子。 $t$ 时刻的奖励是 $R_{t+1}$ ， $t + 1$ 时刻的奖励 $R_{t+2}$ 折现到 $t$ 时刻为 $\gamma R_{t+2}$ ， $t + 2$ 时刻的奖励 $R_{t+3}$ 折现到 $t$ 时刻为 $\gamma^2 R_{t+3}$ ，以此类推， $t + k$ 时刻的奖励 $R_{t+k+1}$ 折现到 $t$ 时刻为 $\gamma^k R_{t+k+1}$ 。

长期回报

在理解了折现因子后，给出长期回报（Return）的定义：
G_t \doteq R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots = \sum_{k=0}^{\infty }\gamma^k R_{t+k+1}
其中 \gamma\in [0,1] ，当 \gamma=0 时，长期回报 G_t=R_{t+1} ；当 \gamma=1 时，长期回报 G_t=R_{t+1}+R_{t+2}+R_{t+3}+\cdots 。也就是说， \gamma 的取值越小，智能体越看中即时奖励； \gamma 的取值越大，智能体越看中长期回报。

值函数

值函数是针对状态或行动的评价函数，具体可分为两种：

状态值函数（State Value Function），是针对状态的评价指标；
行动值函数（Action Value
Function），是针对行动的评价指标。

由于行动是在给定状态下才产生的，一般也将行动值函数更明确地表达为状态-行动值函数（State-Action Value Function）。为了明确起见，接下来的内容将统一使用“状态-行动值函数”。

状态值函数 $v_\pi(s)$ 是给定策略 $\pi$ ，评价状态 $s$ 的指标。具体地，状态值函数 $v_\pi(s)$ 定义为：采用策略 $\pi$ ，从状态 $s$ 开始获得期望回报（Expected Return），即：
$v_\pi(s)\doteq E_\pi [G_t|S_t=s]$

状态-行动值函数 $q_\pi(s,a)$ 是给定策略 $\pi$ ，在状态 $s$ 下评价动作 $a$ 的指标。具体地，状态-行动值函数 $q_\pi(s,a)$ 定义为：采用策略 $\pi$ ，在状态 $s$ 下采用动作 $a$ 获得的期望回报，即
$q_\pi(s,a)\doteq E_\pi [G_t|S_t=s,A_t=a]$