【XJTUSE计算机图形学】第四章 真实感图形学(3)——纹理及纹理映射
本节了解即可
简单光照明模型的缺陷
只能模拟光滑景物表面:
只考虑表面法向的变化;
假设表面反射系数为常数。
如何解决计算机生成真实感图象缺乏现实物体表面细节的问题
引入纹理,增强各种光照明模型生成图像的真实感。
纹理:物体表面的细小结构。
纹理:
最早的工作:Catmull 74年的博士论文,是曲面分割方法中的副产品[Cat74];
可以较好地表达模型表面的细节,而无需考虑其它(几何和材质)细节,使景物更真实。
常见的纹理:
木材表面的木纹;
建筑物墙壁上的装饰图案;
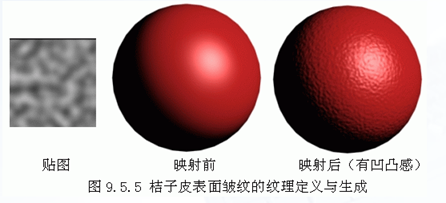
桔子皮表面的皱纹。
纹理概述
使用纹理需要考虑的三个问题:
怎样才能产生纹理效果;
如何定义纹理;
如何进行映射。
1?? 怎样才能产生纹理效果?
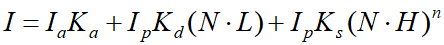
改变反射系数来改变物体的颜色;
改变物体表面的法向量。
2?? 纹理定义:
图像纹理:将纹理图案映射到三维物体表面,绘制物体表面上一点时,采用相应纹理图案中相应的颜色。
函数纹理:用数学函数定义简单的纹理图案;
用数学函数定义随机高度场,生成表面粗糙纹理。
3?? 映射:把纹理图象值映射到三维物体表面的技术
图像纹理:建立二维纹理坐标与三维物体坐标之间的对应关系;
几何纹理:如何扰动法向量。
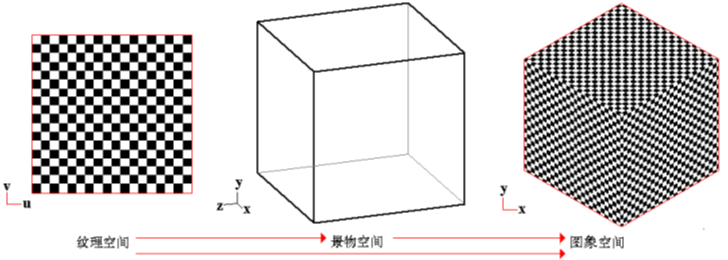
三个空间
纹理空间:纹理通常定义在二维空间(u,v)中的一个矩形区域;
景物空间:物体表面是在三维空间(x,y,z)中的一个曲面,或参数空间 (s∈[0,1],t∈[0,1]),为二维空间的一个矩形区域;
图象空间,图象空间依赖于显示器的分辨率,例如,Nx∈[0,1024],Ny∈[0,768],也是二维空间的一个矩形区域。
二维纹理映射
颜色纹理:实际上是二维数组,元素是一些颜色值(纹理元素或纹理像素)
每个纹理像素在纹理空间中都有一个唯一的地址;
该地址可被认为是一个列和行的值,分别由u和v来表示。
定义方法
1?? 连续法——函数纹理
用数学函数解析地表达,函数的定义域就是纹理空间。
2?? 离散法——图像纹理
用各种数字化图像来离散定义;
纹理空间坐标系中表示光亮度值的矩形数组:
程序生成;
扫描输入;
通过交互式系统绘制得到。
合成纹理
根据给定一个图像示例,合成一种新的纹理;
由于计算机视觉和图形学领域的许多学者均关注于合成纹理方法的研究,因此出现了许多实用的算法。
在计算机图形学中,纹理合成方法可分为两类:
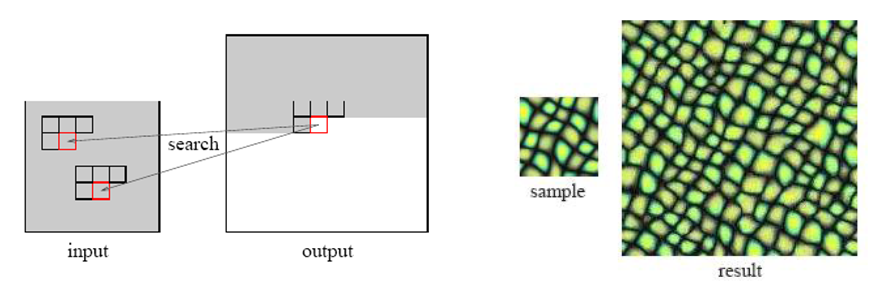
基于像素点的纹理合成方法;
主体思想:逐像素点合成新的纹理图像,其中每个像素点由其周围的像素决定(例如33,55),根据这些周围像素点从原始图像中以最相似的原则从给定的图像示例搜索获得的像素点作为所需的像素点
基于图像块的纹理合成方法。
基于像素点的纹理合成方法计算代价大,通过图像块代替单个像素点的方式,改进纹理合成方法;
Graph-Cut[Kwatra03]是其中一种最重要的方法,它具有非常优越的性能;
选择图像块的原则类似与选择像素点的原则,即仍然基于最相似原则。
映射
纹理映射的实质是建立两个映射关系
从纹理空间到景物空间的映射;
再到屏幕空间的映射。
映射方法
建立物体空间坐标(x,y,z)和纹理空间坐标(u,v)之间的对应关系;
对物体表面进行参数化,反求出物体表面的参数后,根据(u,v)得到该处的纹理值,并用此值取代光照明模型中的相应项,实现纹理映射;
圆柱面映射和球面映射是两个经常使用的映射方法。
圆柱面映射
圆柱面的参数方程
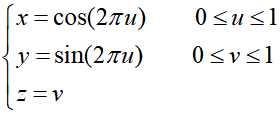
圆柱面上一点(x,y,z)的参数即纹理坐标:
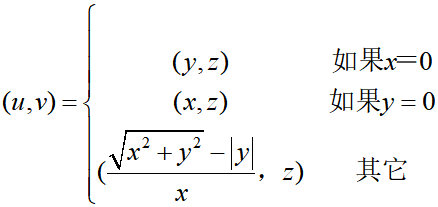

球面映射
球面参数方程
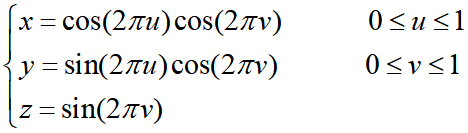
球面上一点(x,y,z)的参数即纹理坐标
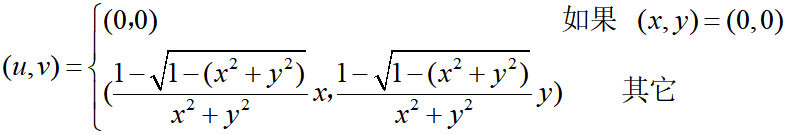
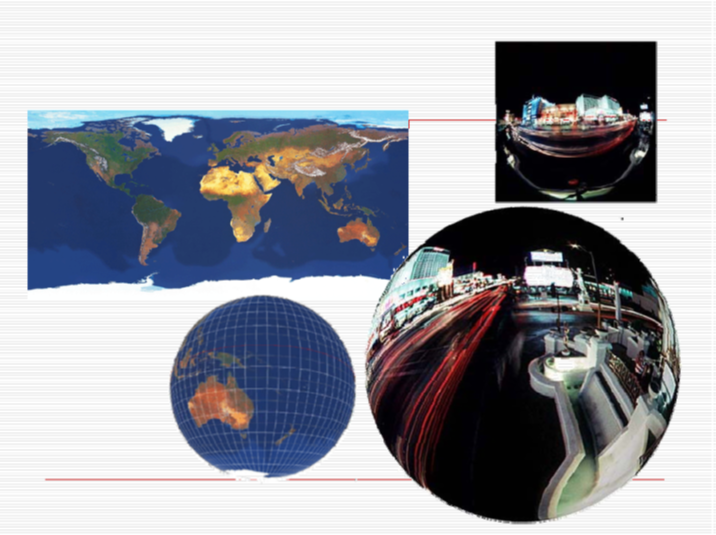
滤波
多个纹理元素只覆盖一个像素单元
最简单的解决方法是点取样,使用最邻近纹理元素:把当前象素单元的最中心所对应的纹理空间的点的值,作为象素的纹理值;这种方式会导致严重的走样。
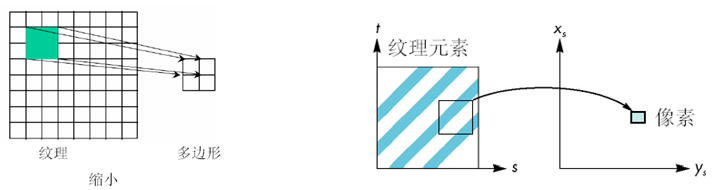
对纹理进行放大,由于采样区域的局限性,所获取的纹理样本通常为小块纹理,将导致映射后表面纹理模糊不清;
若采用重复映射技术,则可能出现表面纹理接缝走样等问题。
为了得到比较合理的像素颜色值
线性滤波器;
Mipmapping(各向同性滤波);
Ripmapping(各向异性滤波)
几何纹理
桔子的模型:
借用图像纹理的思路,将真实桔子的照片贴到球面上模拟桔子;
如果移动了光源或旋转了对象,看到的是桔子的模型的图像,而不是真实桔子的图像;
真实桔子的特征是在表面上有很多小形状变化。
图像纹理不能模拟形状的变化。
几何纹理
1978年,Blinn提出产生几何纹理,模拟凸凹不平的物体表面的方法(凹凸映射,Bump mapping)
基本思想:生成图像时,对曲面的法向量进行扰动。
对景物表面各采样点位置作微小的扰动,改变表面的微观几何形状,引起景物表面法向量的扰动。
景物表面光亮度是法向量的函数:法向量的扰动导致表面光亮度的突变,产生表面凹凸不平的真实效果。
设物体表面上任意一点P(u,v)沿该点处的法向量方向位移F(u,v)个单位长度(N附加一微小增量),从而生成一张新的表面
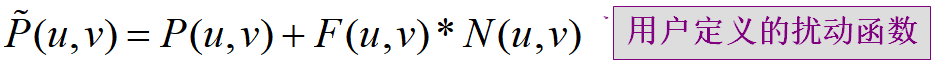
新法向量的计算:
通过对两个偏导数求叉积得到:
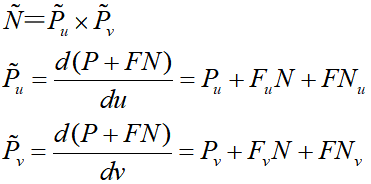
F相对很小, FuFv忽略不计,有:
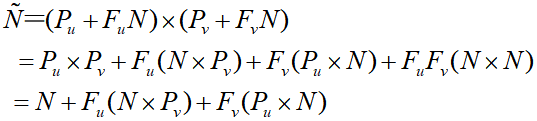
几何纹理的实现
扰动后的法向量单位化,用于计算曲面的明暗度,产生凹凸不平的几何纹理;
几何纹理函数:用二维数组记录各象素的值,图案中较暗颜色对应较小F值,较亮颜色对应较大F值;
F的偏导数的计算,可以用中心差分实现。