引言
本文是光纤布拉格光栅(FBG)的笔记【2】,主要介绍了光纤布拉格光栅的反射率。
光纤布拉格光栅纤芯的平均折射率是 n 0 n_0 n0?,光栅结构周期为 Λ \Lambda Λ(折射率周期性变化故而称为光栅),沿光纤轴向的折射率可以表示为:
n ( z ) = n 0 + Δ n c o s ( 2 π z Λ ) n(z)=n_0+\Delta ncos(\frac{2\pi z}{\Lambda}) n(z)=n0?+Δncos(Λ2πz?)
式中
Δ n \Delta n Δn:折射率扰动的大小(典型值为 1 0 ? 5 ~ 1 0 ? 3 10^{-5}\sim10^{-3} 10?5~10?3);
z z z:沿光纤轴向的位移。
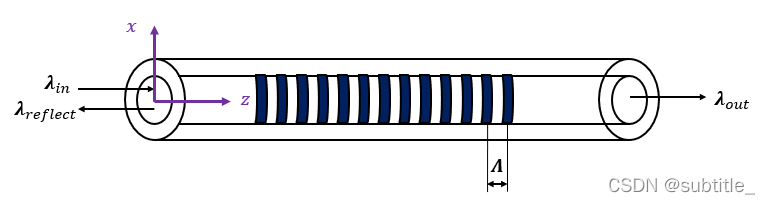
对于一定调制深度和周期的光栅,其反射率可以表示为:
R ( l , λ ) = Ω 2 s i n h 2 ( s l ) Δ k 2 s i n h 2 ( s l ) + s 2 c o s h 2 ( s l ) R(l,\lambda)=\frac{\Omega^2sinh^2(sl)}{\Delta k^2sinh^2(sl)+s^2cosh^2(sl)} R(l,λ)=Δk2sinh2(sl)+s2cosh2(sl)Ω2sinh2(sl)?
式中
R ( l , λ ) R(l,\lambda) R(l,λ):为光栅长度 l l l和波长 λ \lambda λ组成的反射率函数;
Ω \Omega Ω为耦合系数;
Δ k = k ? π / λ \Delta k=k-\pi/\lambda Δk=k?π/λ为失谐量矢量, k = 2 π n 0 / λ k=2\pi n_0/\lambda k=2πn0?/λ为传播常数;
此外 s 2 = Ω 2 ? Δ k 2 s^2=\Omega^2-\Delta k^2 s2=Ω2?Δk2。
从式中可以看出,如果光栅的长度 l l l增加如、折射率改变量 Δ n \Delta n Δn增加,反射率 R ( l , λ ) R(l,\lambda) R(l,λ)也会随之增加。如果沿着光纤轴向折射率的扰动呈正弦变化,则耦合系数 Ω \Omega Ω可以表示为:
Ω = π Δ n λ M p \Omega=\frac{\pi\Delta n}{\lambda}M_p Ω=λπΔn?Mp?
式中
M p M_p Mp?:纤芯导模的能量,由于光栅是被均匀地写入纤芯, M p M_p Mp?可以近似为 1 ? V 2 1-V^2 1?V2, V V V是光纤的归一化频率, V = ( 2 π / λ ) a ( n c o 2 ? n c l 2 ) 1 / 2 V=(2\pi/\lambda)a(n_{co}^2-n_{cl}^2)^{1/2} V=(2π/λ)a(nco2??ncl2?)1/2, a a a为纤芯直径, n c o n_{co} nco?和 c c l c_{cl} ccl?分别为纤芯与包层折射率。
在光纤布拉格光栅的中心波长处,没有波矢量失谐, Δ k = 0 \Delta k=0 Δk=0,反射率的表达式变为:
R ( l , λ ) = t a n h 2 ( Ω l ) R(l,\lambda)=tanh^2(\Omega l) R(l,λ)=tanh2(Ωl)
反射光谱和波长的关系由下图给出:
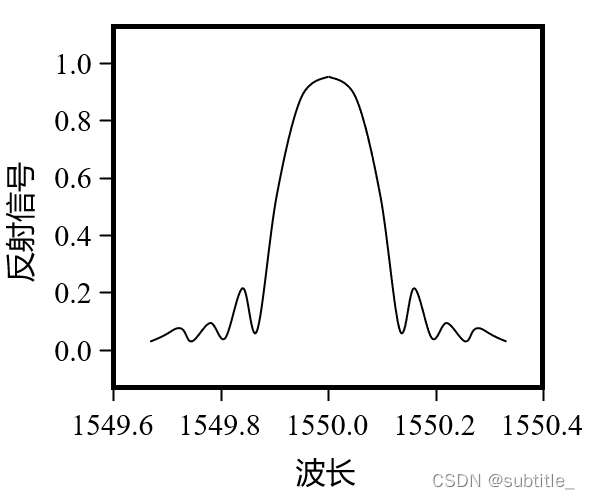
光栅的最大带宽瓣宽度可以近似表示为:
Δ λ = λ B s ( Δ n 2 n 0 ) 2 + ( 1 N ) 2 \Delta \lambda=\lambda_Bs\sqrt{(\frac{\Delta n}{2n_0})^2+(\frac{1}{N})^2} Δλ=λB?s(2n0?Δn?)2+(N1?)2?
式中
N N N:光栅平面的数量
s s s:取决于光栅反射率的大小,如果反射率为100%, s s s约等于1,如果反射率较小, s s s约等于0.5
参考文献:
[1]饶云江 王义平.光纤光栅原理及应用[M].北京:科学出版社,2006:136-137.