狄拉克符号
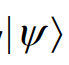 | 箭头为狄拉克记号，右矢 |
|---|---|
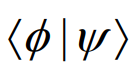 | 表示内积 |
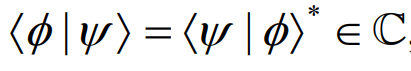 | *表示复共轭 |
狄拉克创立了狄拉克符号系统，使量子力学规律呈现出算符的形式，量子力学得以以更简洁和普遍的形式呈现在我们面前。
算符
算符一般用大写英文字母表示，如
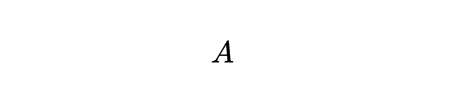
对应于线性代数中的矩阵。
特别的，记单位算符为
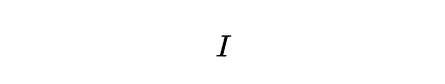
同维的算符间可以相加和相乘，其规律均符合线性代数中矩阵加法和乘法的规律。
态矢
狄拉克符号的态矢分为右矢和左矢，分别用
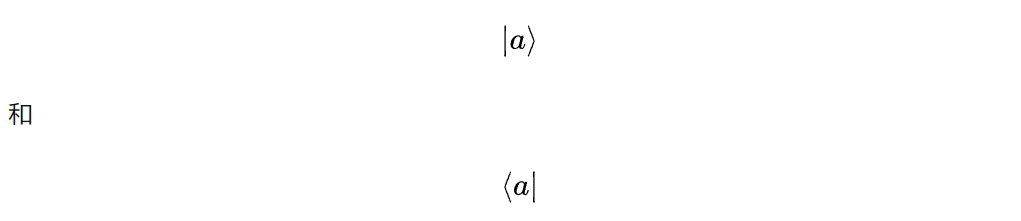
来表示。其中的a可以是任何能够表征这个态的量，如对于能量为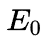
的能量本征态，其态右矢表示往往为
。
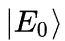态矢与线性代数中的矢量相对应。具体的，右矢往往对应于列矢量，左矢往往对应于行矢量。
同类态矢（即同维右矢或者左矢）间可以做加法。此外，左矢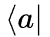
和右矢 
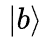间还可以做内积运算，得到的是一个数：
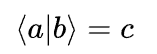这个数一般是复数。
厄米共轭运算
厄米共轭运算是一种一元运算（即只输入一个东西，出来一个东西），运算对象可以是算符，也可以是态矢。算符的厄米共轭仍然是算符，而右矢的厄米共轭变成了左矢，左矢的厄米共轭是右矢。即：
算符A的厄米共轭：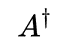
右矢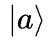
的厄米共轭：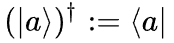
左矢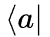的厄米共轭：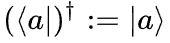
算符A乘算符B的厄米共轭：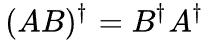
态矢间内积的厄米共轭：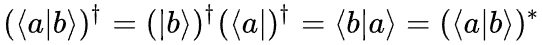
算符乘右矢的厄米共轭：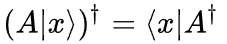
特别的，定义复数a的厄米共轭：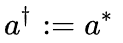
即复数的厄米共轭就定义为它的复共轭。（其实这不是一种特别的定义，因为数可以看成是1维矩阵）
厄米算符和幺正算符
一般来说，算符A的厄米共轭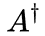
是不同于A的另一个算符B。然而，如果 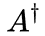正好等于A，那么我们称这种算符为厄米算符。可以证明，厄米算符的本征值必为实数，因此所有可观测的物理量对应的算符必然是厄米算符。
如果有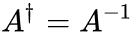
，那么A被称为幺正算符。因为 
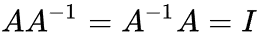，所以对于幺正算符来说有
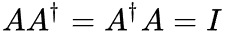，这也意味着幺正算符作用于态矢上不改变态矢的“长度”。
本征方程
对于算符A，如果存在态矢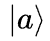 
使得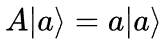
其中a是一个数，那么以上方程就是A的一个本征方程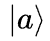， 是A的一个本征矢，a是A的一个对应于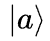的本征值。
算符的矩阵元
我们知道，量子力学又被称为矩阵力学，力学量常常用矩阵来表示。抽象的算符是如何变成具体的矩阵的呢？下面介绍这一过程。
首先，假设我们有一套完备的基矢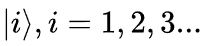
现在我们想要将算符A用矩阵表达，可以利用这套基矢，定义：
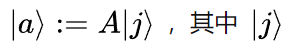是这套基矢中的一个基矢。
另一方面，我们看内积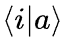 
它是一个数，已经具有了矩阵元的性质，不妨就把它作为A的一个矩阵元。
为了写出内积，每次都定义 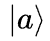太麻烦了，不妨直接把内积 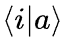写成：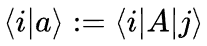
这正是算符A的第i行，第j列的矩阵元。
讨论：
下面考察矩阵元的共轭：
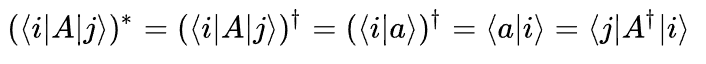
这个式子翻译过来就是：A的第i行第j列元素的复共轭，正等于 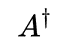的第j行第i列元素。这正是矩阵的厄米共轭的定义，也从一个侧面反映出来为什么矩阵运算与算符运算是相容的。
通过以上过程，我们可以看到一个重要的细节：想要将算符表示为矩阵，必须要选取一组完备基矢。这也就意味着同一个算符可以依选取基矢组的不同表示为不同的矩阵，完备基矢间的变换被称为幺正变换。
态矢组成的算符
狄拉克符号中算符也可以由态矢组成，如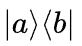
就是一个算符。其定义方式如下：
将算符 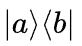写成A。那么A对任意右矢 
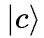的作用均定义为：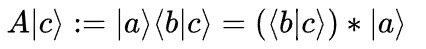
即作为数的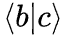 
数乘以态矢 。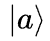
特别的，正交完备基矢组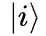 
可以以这种方式组成单位算符：
这一点非常重要，在量子力学的运算中处处可见。
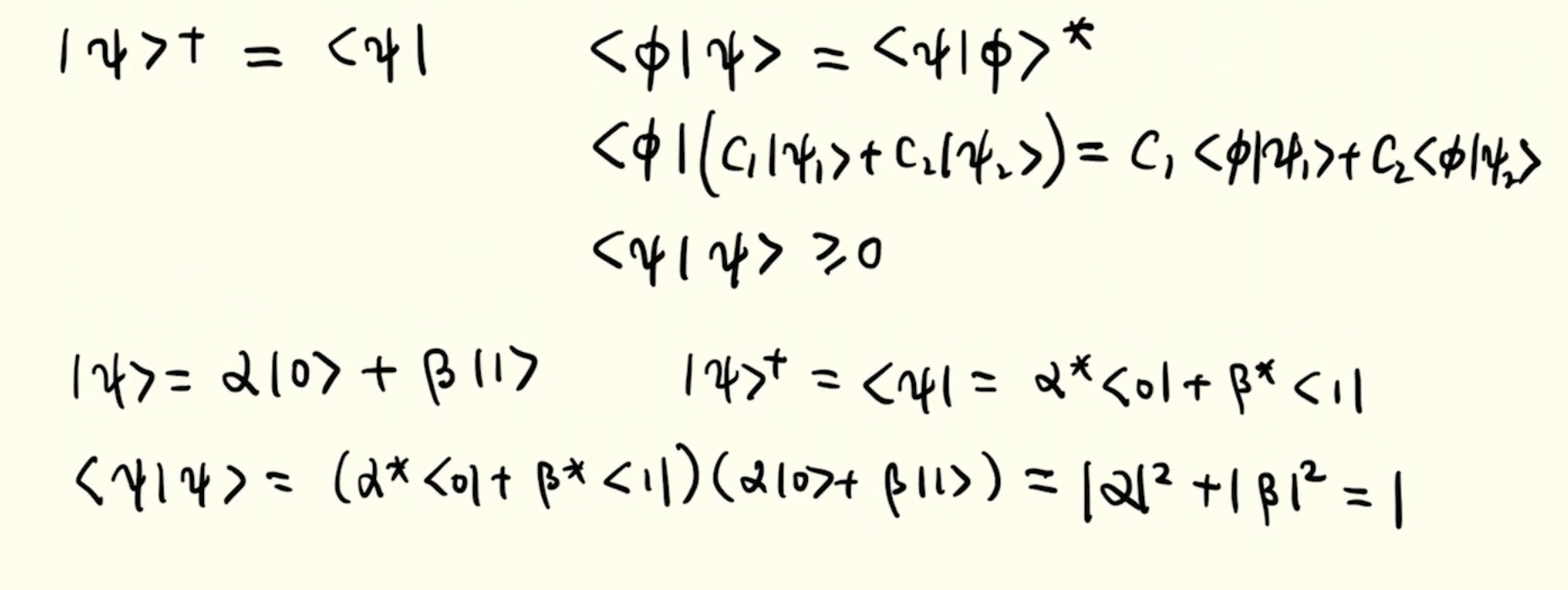
矢量与矢量空间
重要概念
线性独立；对偶矢量；内积；正交归一
完备集；基
基展开后算内积；模
柯西-施瓦茨不等式:
线性算符；算符的和与积；矩阵表示
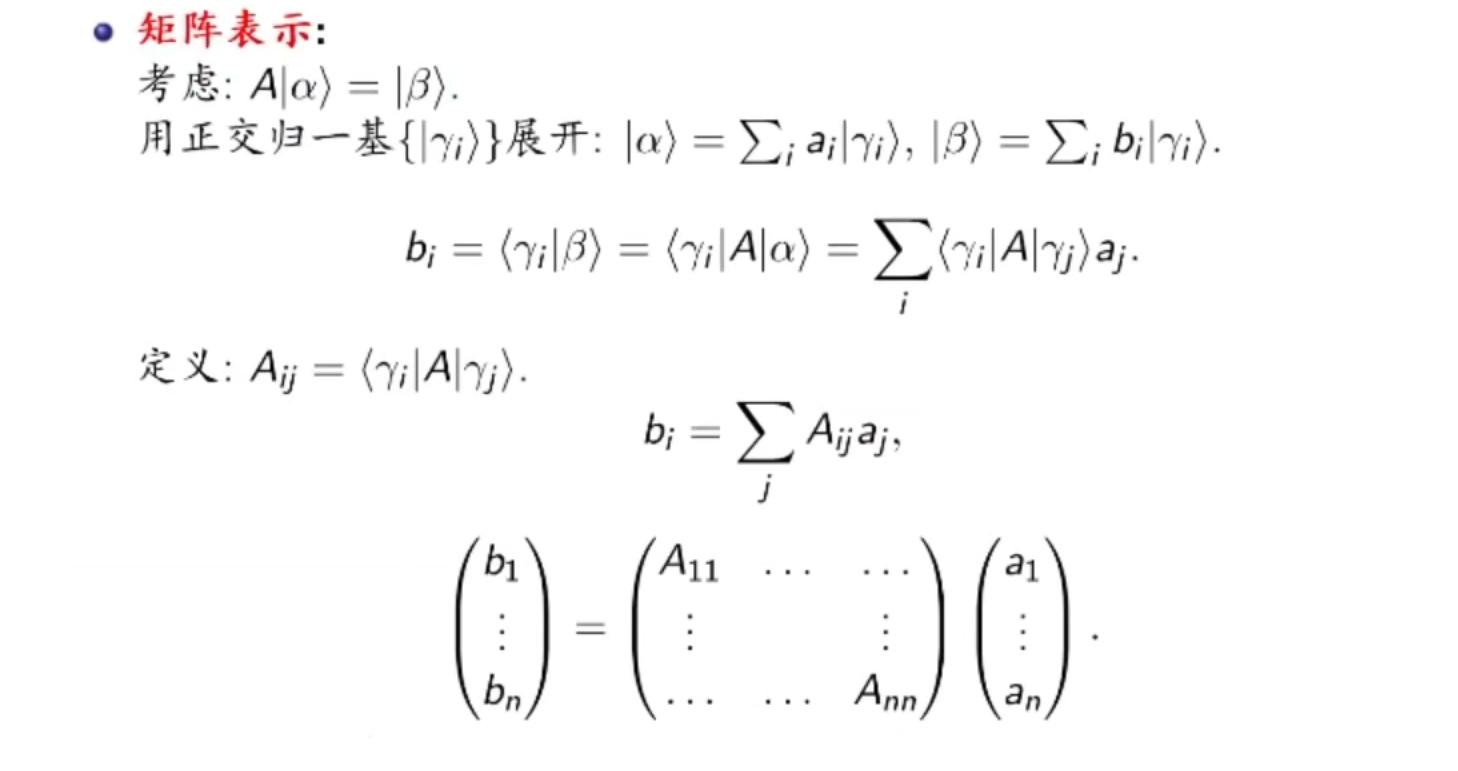
泡利矩阵；逆算符
投影算符
正交化
完备性关系
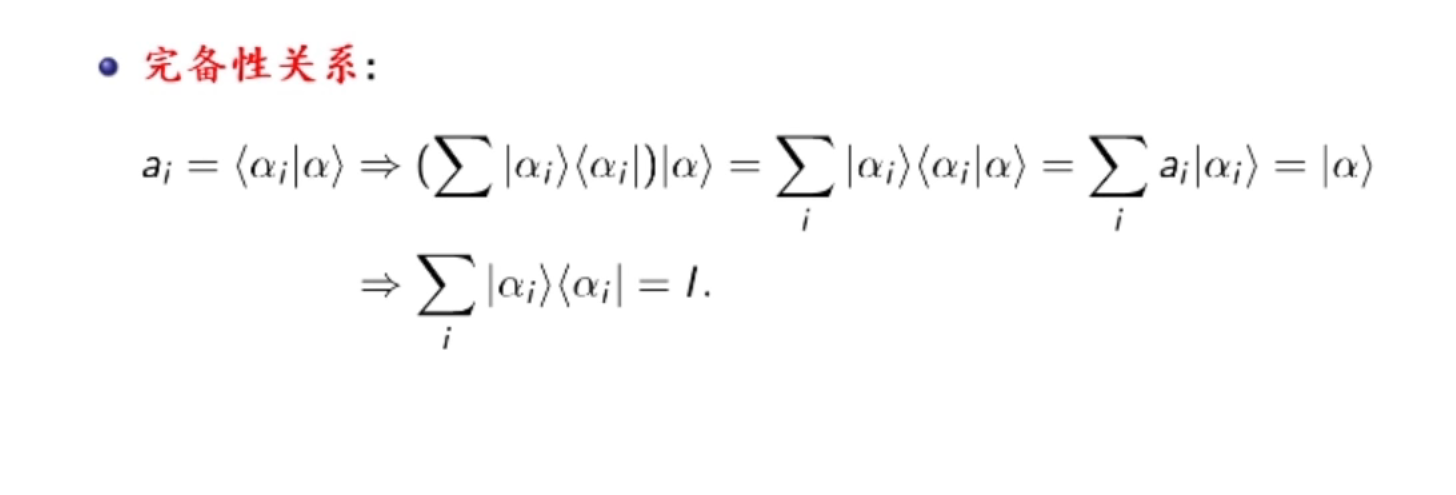
本征值与本征矢
厄密算符
厄密算符的本征矢量
量子力学基本假设
幺正算符U
基失变换
算符的对角表示
什么情况下可以对角化
032)]
[外链图片转存中…(img-FhKXaNKn-1645106252032)]
算符的对角表示
[外链图片转存中…(img-zYFEncRT-1645106252033)]
什么情况下可以对角化
[外链图片转存中…(img-D8I6ZVXC-1645106252033)]