[人工智能]tensor中线性代数表示

标量

直接一维表示，例如torch.tensor(2.0)
当为一维向量的时候，torch默认为行向量

向量

访问张量长度len()、.shape

矩阵

通过指定两个分量 m 和 n 来创建一个形状为 m×n 的矩阵。
例如A = torch.arange(20).reshape(5, 4)
tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15], [16, 17, 18, 19]])

转置A.T

张量

Hadamard积（Hadamard product）数学符号 ⊙

向量是标量的推广，矩阵是向量的推广一样，我们可以构建具有更多轴的数据结构。 张量（本小节中的“张量”指代数对象）为我们提供了描述具有任意数量轴的 n 维数组的通用方法。

降维

A.sum(axis=0)行降维，向上压缩成一行的数组
A.sum(axis=1)列降维，向右压缩成一列…
降维后运算要注意广播机制

点积

torch.dot(x,y)
torch.sum(x*y)

向量积

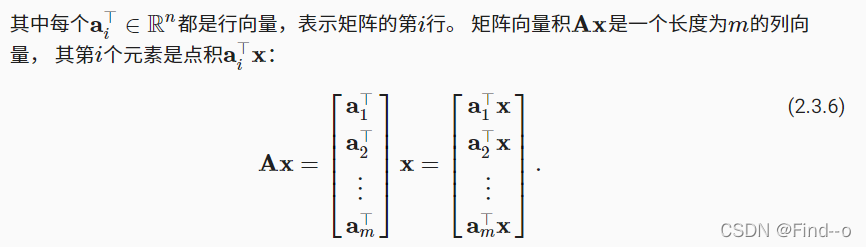
在代码中使用张量表示矩阵-向量积，我们使用与点积相同的mv函数。 当我们为矩阵A和向量x调用torch.mv(A, x)时，会执行矩阵-向量积。 注意，A的列维数（沿轴1的长度）必须与x的维数（其长度）相同。
A.shape, x.shape, torch.mv(A, x)

矩阵乘法

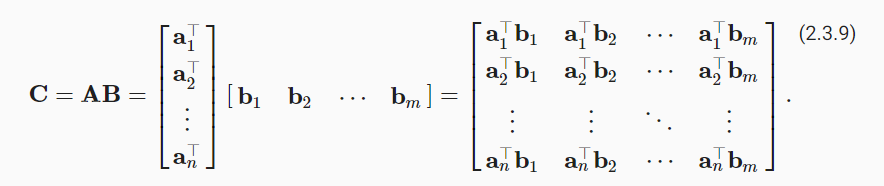
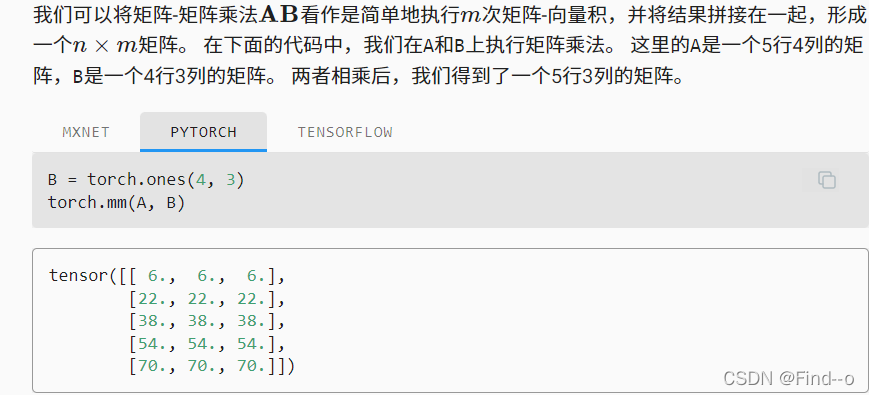
范数

L2范数

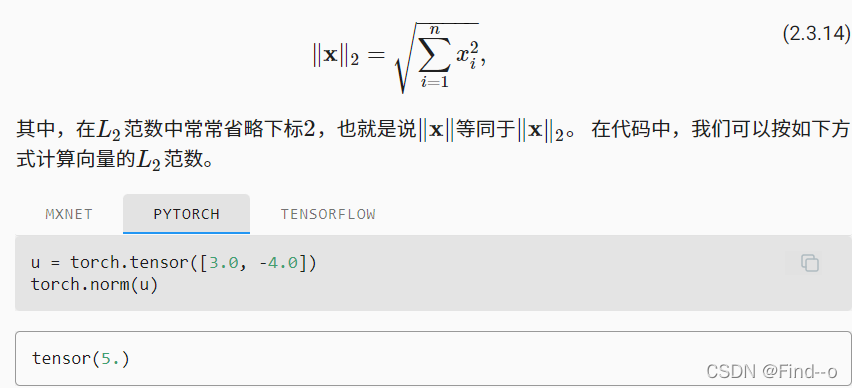
L1范数

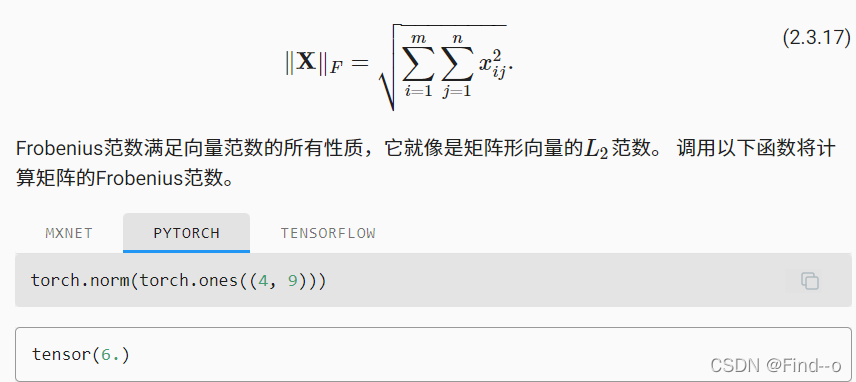
Frobenius范数

动手学深度学习2.3.13练习

1. 证明一个矩阵 A 的转置的转置是 A ，即 (A?)?=A 。

2. 给出两个矩阵 A 和 B ，证明“它们转置的和”等于“它们和的转置”，即 A?+B?=(A+B)? 。

3. 给定任意方阵 A ， A+A? 总是对称的吗?为什么?

   对称
   

4. 我们在本节中定义了形状 (2,3,4) 的张量X。len(X)的输出结果是什么？

    2，len(x)是第一维的长度
   

5. 对于任意形状的张量X,len(X)是否总是对应于X特定轴的长度?这个轴是什么?

6. 运行A/A.sum(axis=1)，看看会发生什么。你能分析原因吗？

    当行列维度不相同时候，a.sum(axis=1)对每一行数组求和，A=（m,n）就会变成长度为n的形式,，而A中长度为m，长度不匹配，无法计算
   

7. 考虑一个具有形状 (2,3,4) 的张量，在轴0、1、2上的求和输出是什么形状?

    机
   

8. 为linalg.norm函数提供3个或更多轴的张量，并观察其输出。对于任意形状的张量这个函数计算得到什么?