SIFT 特征点算法
通过不同模糊程度的灰度图相减找极值 ,筛选确定出真实关键点后按梯度和权重求出关键点的主方向,再给关键点附近的16个区块确定8方向矢量,相当于给这幅图的这个位置做个特征标记【类比特征向量】。于是能通过这些特征标记寻找出两图对应的特征点,从而通过多个对应特征点确定图像变换矩阵。
即,Sift是一种基于尺度空间的,对图像缩放、旋转、甚至仿射变换保持不变性的图像局部特征描述算子。缺点是实时性不高,并且对于边缘光滑目标的特征点提取能力较弱。

【SIFT实例】 目标识别及VLFeat开源库 --代码君CodeSama
尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视觉的算法,用来侦测与描述影像中的局部性特征,它在空间尺度中寻找极值点,并提取出其位置、尺度、旋转不变量。SIFT所查找到的关键点是一些十分突出且不会因光照、仿射变换和噪音等因素而变化的点,如角点、边缘点、暗区的亮点及亮区的暗点等,对于光线、噪声、些微视角改变的容忍度相当高。
SIFT算法可以解决的问题:
目标的自身状态、场景所处的环境和成像器材的成像特性等因素影响图像配准/目标识别跟踪的性能。而SIFT算法在一定程度上可解决:
- 目标的旋转、缩放、平移(RST)
- 图像仿射/投影变换(视点viewpoint)
- 光照影响(illumination)
- 目标遮挡(occlusion)
- 杂物场景(clutter)
其应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。
SIFT算法分解为如下四步:
6. 尺度空间极值检测:搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。【用高斯滤波获取尺度空间。(用两次一维的高斯卷积将消除二维高斯矩阵所产生的边缘,还比二维高斯卷积的计算量少)。将图像金字塔每层的一张图像使用不同参数的高斯模糊(这里的公式是关键),使得金字塔的每层含有多张(6-8张)高斯模糊图像。在高斯金字塔中一共生成O组L层不同尺度的图像,这两个量合起来(O,L)就构成了高斯金字塔的尺度空间,即给定的一组坐标(O,L)就可以唯一确定高斯金字塔中的一幅图像。
把模糊后的图像两两相减(另外起名叫DoG空间),Dog空间里的图像是用来寻找极值点的原始数据。
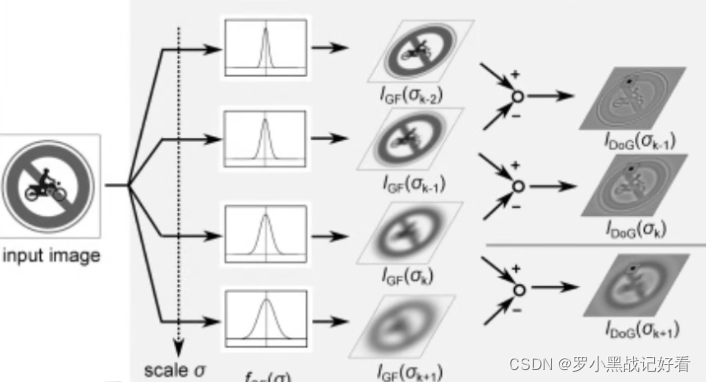
依据Dog空间里的相邻图片检测极值点
极值点公式:(式中σ是尺度空间坐标)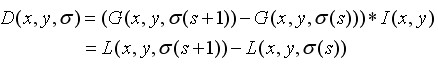
-
关键点定位:第一步检测到的极值点是作为候选的离散空间的极值点,这步通过拟合三维二次函数来精确确定关键点的位置和尺度【对上图的D公式求偏导 求得连续空间下的真实极值点的像素位置(如果x、y或者σ偏离了0.5以上就换位置重新进行插值计算】,同时去除低对比度的关键点和不稳定的边缘响应点【超出迭代次数或者极值D过低属于噪声】。
-
方向确定:相对像素的亮度值,梯度对光照具有更好的鲁棒性。基于图像局部的梯度方向,分配给每个关键点位置一个或多个主方向。
计算关键点周围一定区域的梯度值,比如8*8区域。
1、然后将得到的角度值进行36等分。
2、在特征点对应的尺度空间计算梯度值。
3、利用高斯核对梯度进行计算权重。

建立一个36维的直方图,每次累加的值就是它的权重。大于主方向峰值80%的方向作为该关键点的辅方向【仅有15%的关键点被赋予多个方向】
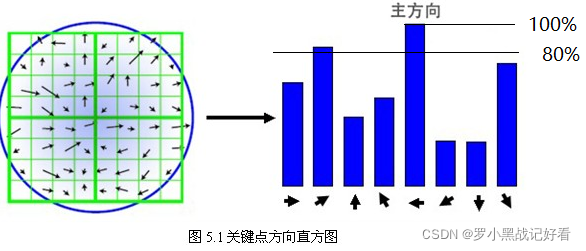
-
关键点描述:再在选择完主方向后,通过对关键点周围图像区域分块,记录16个种子点【在下文提及】的方向 并以主方向计算相对角度。这样就算图像进行旋转,主方向也会进行旋转,相对角度保持相对恒定状态,即使有比较大的局部形状的变形和光照变化也不会受到影响。
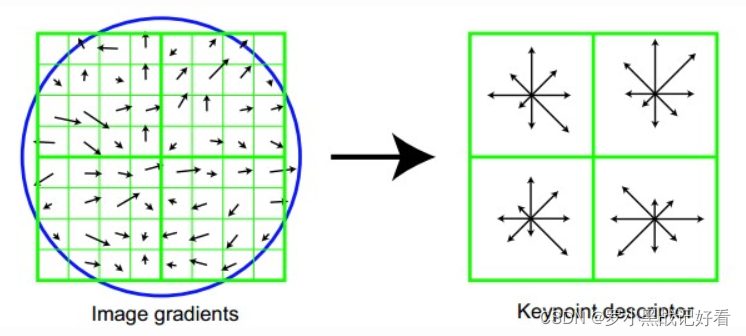
左图的中央为当前关键点的位置,每个小格代表为关键点邻域所在尺度空间的一个像素,求取每个像素的梯度幅值与梯度方向。4*4个一组,依据高斯加权计算每个梯度方向的累加值,即可形成一个种子点【配图右侧是4个种子】,每个种子点有8个方向的向量信息。这种邻域方向性信息联合增强了算法的抗噪声能力,同时对于含有定位误差的特征匹配也提供了比较理性的容错性。每个关键点使用4×4共16个种子点来描述,这样一个关键点就可以产生128维的SIFT特征向量。这个128维的SIFT特征向量就像是我们每个人的身份证一样,拥有绝对标识,几乎不可能重复,在这里可以对128维向量进行归一化处理,可以去除光照变化的影响。我们对模板图和目标图分别建立描述子集合。 -
特征点匹配:
特征点的匹配是通过计算两组特征点的128维的特征点的欧氏距离实现的。欧氏距离越小,则相似度越高,当欧式距离小于设定阈值时,可以判定为匹配成功。
基础知识
图像金字塔、高斯金字塔、差分金字塔(DOG金字塔)、尺度空间、DoG (Difference of Gaussian)角点检测
Surf算法
与Sift算法一样,Surf算法的基本路程可以分为三大部分:局部特征点的提取、特征点的描述、特征点的匹配。 但Surf在执行效率上有两大制胜法宝——一个是积分图在Hessian(黑塞矩阵)上的使用,一个是降维的特征描述子的使用。 为算法在实时计算机视觉系统中应用提供了可能。
Surf改进了特征的提取和描述方式
-
构建Hessian(黑塞矩阵),生成所有的兴趣点,用于特征的提取;
在构造Hessian矩阵前需要对图像进行高斯滤波,构建Hessian矩阵的过程对应于Sift算法中的高斯卷积过程。
降低滤波器精度
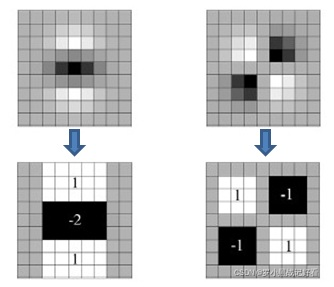
-
构建尺度空间
不在组与组之间改变图像大小,而是改变滤波器的模板尺寸的大小。 -
特征点定位
一样 -
特征点主方向分配
统计60度扇形内所有点的水平、垂直haar小波特征总和,最后将值最大的那个扇形的方向作为该特征点的主方向。该过程示意图如下: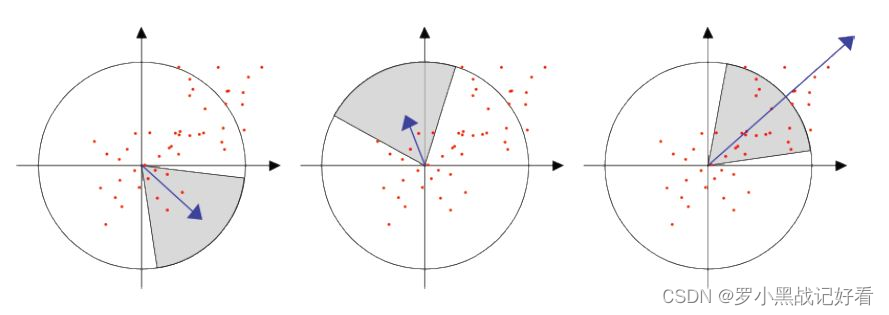
-
生成特征点描述子
用4个值作为每个子块区域的特征向量【sift是8个】该haar小波特征为水平方向值之和、垂直方向值之和、水平方向绝对值之和以及垂直方向绝对值之和。一个特征点有16*4=64维向量。 -
特征点匹配
Surf也是计算两个特征点间的欧式距离来确定匹配度。Surf还加入了Hessian矩阵迹的判断,如果两个特征点的矩阵迹正负号相同,代表这两个特征具有相同方向上的对比度变化,如果不同,说明这两个特征点的对比度变化方向是相反的,即使欧氏距离为0,也直接排除。
基础知识
小波变换一之Haar变换