参考链接:
https://zhuanlan.zhihu.com/p/68468520
一、目的
损失函数用来衡量机器学习模型的精确度。一般来说,损失函数的值越小,模型的精确度就越高。如果要提高机器学习模型的精确度,就需要尽可能降低损失函数的值。而降低损失函数的值,我们一般采用梯度下降这个方法。所以,梯度下降的目的,就是为了最小化损失函数。
如损失函数MSE,见公式(1):
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wq1b2Aiq-1645770279138)(https://www.zhihu.com/equation?tex=L%28w,b%29%20=%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi=1%7D%5E%7BN%7D%7B%28y_%7Bi%7D%20-%20f%28wx_%7Bi%7D%20%2b%20b%29%29%5E%7B2%7D%7D#pic_center)]](https://img-blog.csdnimg.cn/723bd71b81d3403e89ad8523fcda10b7.png)
二、原理
寻找损失函数的最低点,就像我们在山谷里行走,希望最快的方式找到山谷里最低的地方。在现实中,我们是寻找下降速度最快的一个方式。很显然,如果步速一致的时候,在相同的时间,坡最陡峭的方向是下降速度最快的。
- 最陡峭的方向—>梯度方向

一个样本对应着一个梯度 d L d w \frac{d L}{dw} dwdL?,那么多个样本对应多个梯度。获得平均梯度 d L w ˉ \frac{dL}{\bar{w}} wˉdL?当作整体样本的梯度。(可看作多个样本的”决策“平衡后的结果。)上图所示为只有一个权重 w w w,权重 w w w的方向就只有向左和向右之分。假设样本A每隔一定时间,观察一次最陡峭得方向,并沿着其方向前进。因此样本A在步速固定得情况下,其固定时间得步长s是相同得。那么权重 w w w得改变量为 Δ w = s ? d L d w \Delta w=s* \frac{d L}{d w} Δw=s?dwdL?(其中,上图所示 d L d w = c o s θ \frac{dL}{dw}=cos \theta dwdL?=cosθ)
- 相同的时间*相同的步速==相同的路程—>学习率
因此下一个时刻得权重得更新值为: w + ∣ Δ w ∣ w+|\Delta w| w+∣Δw∣.对应到数学语言上来说,用 w i w_i wi? 表示权重的初始值, w i + 1 w_{i+1} wi+1? 表示更新后的权重值,用 α \alpha α 表示学习率,则有 公式(2)
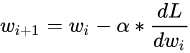
在梯度下降中,我们会重复式子(2)多次,直至损失函数值收敛不变。
如果学习率
α
\alpha
α设置得过大,有可能我们会错过损失函数的最小值;如果设置得过小,可能我们要迭代式子(2)非常多次才能找到最小值,会耗费较多的时间。因此,在实际应用中,我们需要为学习率
a
l
p
h
a
alpha
alpha 设置一个合适的值。
上面讲解了对权重
w
w
w 值的优化过程,对于偏差
b
b
b,我们也可以用相同的方式进行处理,这里就不再展开了。
三、梯度下降过程

四、其他梯度下降算法
1. 小批量样本梯度下降(Mini Batch GD)
这个算法在每次梯度下降的过程中,只选取一部分的样本数据进行计算梯度,比如整体样本1/100的数据。在数据量较大的项目中,可以明显地减少梯度计算的时间。
2. 随机梯度下降(Stochastic GD)
随机梯度下降算法只随机抽取一个样本进行梯度计算,由于每次梯度下降迭代只计算一个样本的梯度,因此运算时间比小批量样本梯度下降算法还要少很多,但由于训练的数据量太小(只有一个),因此下降路径很容易受到训练数据自身噪音的影响,看起来就像醉汉走路一样,变得歪歪斜斜的