[人工智能]理解误差反向传播&用python实现自动微分

理解误差反向传播&用python实现自动微分

使用计算图理解误差反向传播

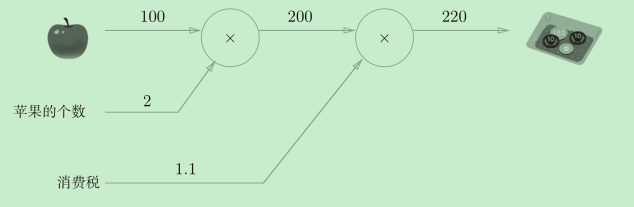
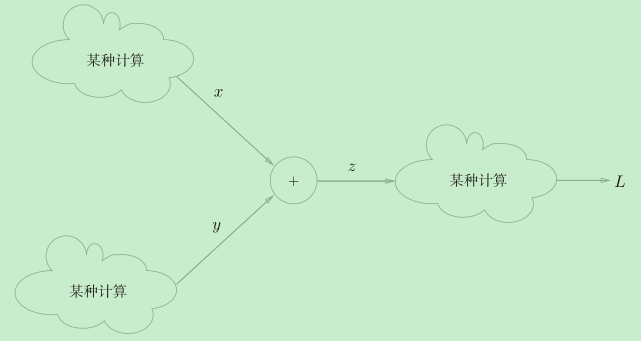
这张图展示了一个从左向右的计算流程，看起来很简单是不是。这种“从左向右进行计算”是一种正方向上的传播，称为正向传播（forward propagation）。而像下图中那样反过来“从右向左进行计算”是一种反方向上的传播，称为反向传播（backward propagation）。

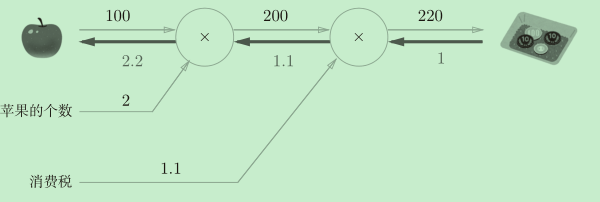
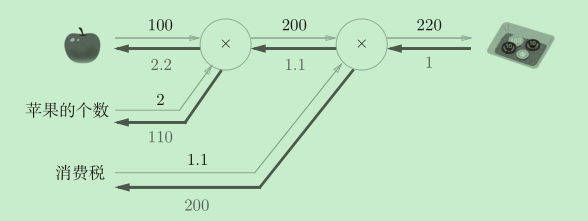
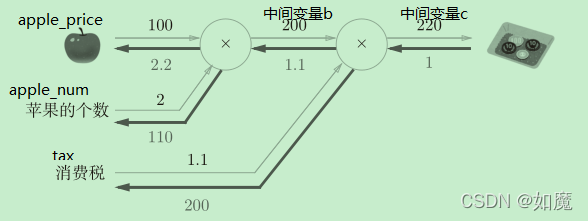
加粗横线就是反向传播的途径。反向传播会传递“局部导数”——也就是写在加粗横线下面的数字。从图中我们可以清晰地看到“支付金额“关于”苹果的价格“的导数的值是2.2。无论多么复杂的计算，都可以讲它拆分为一个一个单独地计算（加减乘除）然后用这种方式清楚地计算出导数。

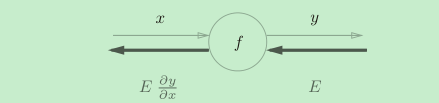
如图，对于任意一个简单计算函数f，我们都可以很轻松的计算出反向传播输出的局部导数值。如图，在反向传播中E是流入f的值（输入），Edy/dx是流出f的值（输出）。反向传播的计算规则是，将信号E乘以节点的局部导数（dy/dx），然后将结果传递给下一个节点。

误差反向传播

• 为什么反向传播能够计算导数呢？

如上图苹果的例子所示，我们把苹果的价格当做自变量x，那么支付金额y = f(x) = 苹果的个数*消费税*x。

那么“支付金额”关于“苹果价格”的导数就是：df/dx = 苹果的个数*消费税。

在图中的表示就是经过两个”乘法计算“最终得到2*1.1=2.2。

• 为什么叫误差反向传播呢？

因为在神经网络中，正向传播的终点、反向传播的起点是损失函数值（误差），我们要求得也是损失函数值关于各个参数的梯度（很多偏导数组成的向量）。

加法节点的反向传播

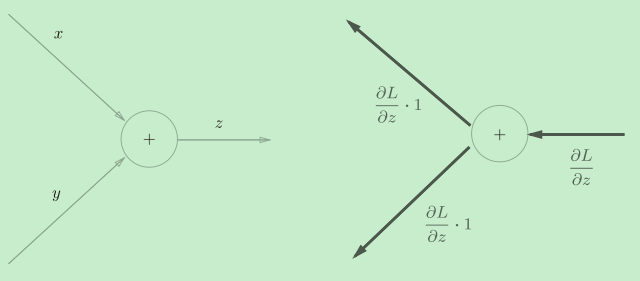
加法节点的反向传播将输入的值会原封不动地流向下一个节点。

乘法节点的反向传播

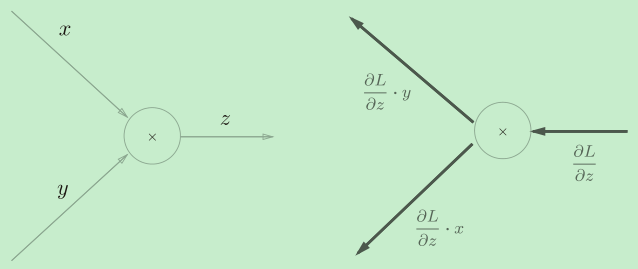
乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。

举个例子

y=1/x的反向传播

反向传播时，会将上游的值乘以?y²（正向传播的输出的平方乘以?1后的值）后，再传给下游。

计算图的优点

1. 局部计算，每个“计算”只需要按照规则将上游的输入经过简单的计算后，传递给下一个“计算即可。

2. 将中间的计算结果全部保存起来，如上面例子所示，在反向传播中会用到正向传播时的两个输入x和y，因此就需要这个“计算”将中间结果保存起来，而一旦在代码中实现这样的一个一个“计算”，那就实现了自动微分。

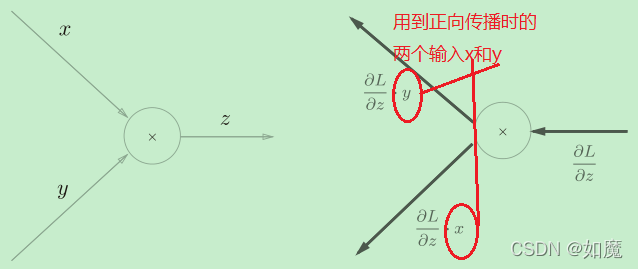
自动微分

pytorch中实现了tensor类来实现自动微分，这里我们自己实现一个简单的自动微分。

_{部分代码参考《Python深度学习入门：从零构建CNN和RNN》}

首先我们定义了一个Numberable包括了用于计算的整数和浮点数，便于统一计算。ensure_number用于把int和float类型装换为Numberable类型。

from typing import *

Numberable = Union[float, int]

def ensure_number(num: Numberable):
    # isinstance: Return whether an object is an instance of a class or of a subclass thereof
    if isinstance(num, NumberWithGrad):
        return num
    else:
        return NumberWithGrad(num)

这就是我们用于实现自动微分的类了，它保存正向传播时的中间结果（depends_on)用于反向传播时使用，还保存反向传播的局部梯度(grad)。

class NumberWithGrad(object):
     def __init__(self,num: Numberable,depends_on: List[Numberable] = None,creation_op: str = ''):
         # 本身的值
         self.num = num
         # 对应的局部梯度
         self.grad = None
         # 它所参与的“计算”需要用到的正向传播中的输入
         self.depends_on = depends_on or []
         # 计算类型标识
         self.creation_op = creation_op

     # 在 Python 中，使用 + 或 – 等运算符实际上会调用 _add_ 或 _sub_ 之类的基础隐藏方法,所以我们要重写这两个方法
     def __add__(self,other: Numberable):
         # 进行加法计算
        return NumberWithGrad(self.num + ensure_number(other).num,depends_on = [self, ensure_number(other)],creation_op = 'add')

     def __mul__(self,other: Numberable = None):
         # 进行乘法计算
        return NumberWithGrad(self.num * ensure_number(other).num,depends_on=[self, ensure_number(other)],creation_op='mul')

     def backward(self, backward_grad: Numberable = None) -> None:
         if backward_grad is None:
             # 反向传播最开始的梯度设为1
             self.grad = 1
         else:
             # 这些行允许累积梯度。
             # 如果梯度尚不存在，就将其设置为backward_grad
             if self.grad is None:
                 self.grad = backward_grad
             # 否则，只需向现有梯度添加backward_grad
             else:
                 self.grad += backward_grad

         if self.creation_op == "add":
             # 加法节点的反向传播将输入的值会原封不动地流向下一个节点
             self.depends_on[0].backward(self.grad)
             self.depends_on[1].backward(self.grad)

         if self.creation_op == "mul":
             # 乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。

             # 计算关于第1个元素的导数
             new = self.depends_on[1] * self.grad
             # 向后发送关于该元素的导数
             self.depends_on[0].backward(new.num)
             # 计算关于第2个元素的导数
             new = self.depends_on[0] * self.grad
             # 向后发送关于该元素的导数
             self.depends_on[1].backward(new.num)

我们接下来使用自动微分功能计算苹果例子中的导数：

apple_price = NumberWithGrad(100)
apple_num = NumberWithGrad(2)
tax = NumberWithGrad(1.1)

b = apple_price * apple_num
c = b * tax

#这里只需要调用c.backward(),即可计算出上面所有变量再反向传播中的梯度了。
c.backward()

print("apple_price.grad=",apple_price.grad)
print("apple_num.grad=",apple_num.grad)
print("tax.grad=",tax.grad)
print("中间变量b.grad=",b.grad)
print("中间变量c.grad=",c.grad)

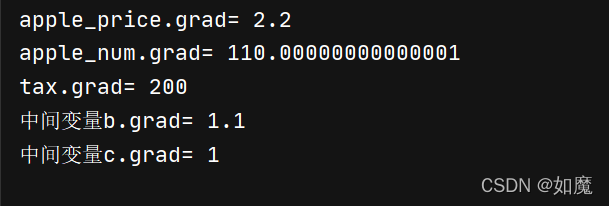
可以看到，这跟我们在计算图中推到的结果一致。

下面用自动微分解决一个难一点的问题：计算Sigmoid函数的导数

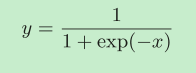
这次的难点主要是包含了除法和指数运算，我们需要在原有的代码上添加对除法运算和指数运算的自动微分支持。

在NumberWithGrad类中添加方法

def div(self,other: Numberable = None):
   # 进行除法计算
   return NumberWithGrad(self.num / ensure_number(other).num,depends_on=[self, ensure_number(other)],creation_op='div')

def exp(self):
   # 进行指数计算
   return NumberWithGrad(math.exp(self.num),depends_on=[self],creation_op='exp')

在backward方法的最后添加条件判断

if self.creation_op == "div":
    # 除法z=x/y的反向传播。

    # 计算关于x的导数 dz/dx = 1/y
    new = ensure_number(1/self.depends_on[1].num * self.grad)
    # 向后发送关于该元素的导数
    self.depends_on[0].backward(new.num)

    # 计算关于y的导数 dz/dy = x*-(1/y)**2
    new = ensure_number(-1 * self.depends_on[0].num * (1/self.depends_on[1].num) * (1/self.depends_on[1].num) * self.grad)
    # 向后发送关于该元素的导数
    self.depends_on[1].backward(new.num)

if self.creation_op == "exp":
    # 指数函数y=exp(x)的反向传播。

    # 计算关于x的导数 dy/dx = exp(x)
    new = ensure_number(math.exp(self.depends_on[0].num) * self.grad)
    # 向后发送关于该元素的导数
    self.depends_on[0].backward(new.num)

使用如下代码进行自动微分：（dl/dy默认是1，并且设x=2）

# Sigmoid
x=NumberWithGrad(2)
num_f1=NumberWithGrad(-1)
num_1_1=NumberWithGrad(1)
num_1_2=NumberWithGrad(1)

b=x*num_f1
c=b.exp()
d=c+num_1_1
y=num_1_2.div(d)
y.backward()

print("x.grad=",x.grad)

下图是用计算图推导的反向传播过程,我们来验证一下自动微分的结果。

y=1/(1+math.exp(-2))
x_grad=1 * y * y * math.exp(-2)
print(x_grad)

结果一致，说明我们设计的自动微分工具可以正常的自动求出sigmoid函数的微分！！！！

最后放在一张图，是我关于神将网络中误差反向传播的理解