原理
| 算法 | 说明 | 特点 |
|---|---|---|
| ID3 | 信息增益 | |
| C4.5 | todo | |
| CART | todo |
公式
信息熵
H ( X ) = ? ∑ i = 1 n P ( x i ) log ? 2 P ( x i ) H(X)=-\sum\limits_{i=1}^nP(x_i)\log_2P(x_i) H(X)=?i=1∑n?P(xi?)log2?P(xi?)
条件熵
H ( X ∣ Y ) = ∑ y P ( y ) H ( X ∣ Y = y ) = ? ∑ y P ( y ) ∑ x P ( x ∣ y ) log ? 2 ( P ( x ∣ y ) ) \begin{aligned} H(X|Y) &=\sum\limits_yP(y)H(X|Y=y) \\ &=-\sum\limits_yP(y)\sum\limits_xP(x|y)\log_2(P(x|y)) \end{aligned} H(X∣Y)?=y∑?P(y)H(X∣Y=y)=?y∑?P(y)x∑?P(x∣y)log2?(P(x∣y))?
ID3算法
数据集
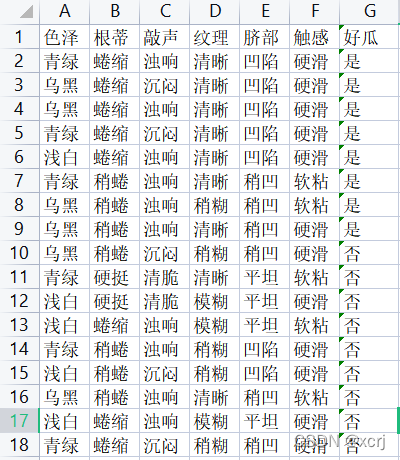
分析
- 特征(feature)=(输入X):第一行(除了好瓜)
- 标签(label)=(输出y):最后1列(除了好瓜)
信息增益
给定特征的信息增益=数据集的信息熵-给定特征的条件熵
数据集的信息熵:所有特征对应标签(输出)的信息熵之和
H
(
D
)
=
?
∑
k
=
1
K
∣
L
k
∣
∣
D
∣
log
?
2
∣
L
k
∣
∣
D
∣
H(D)=-\sum\limits_{k=1}^K\frac{|L_k|}{|D|}\log_2\frac{|L_k|}{|D|}
H(D)=?k=1∑K?∣D∣∣Lk?∣?log2?∣D∣∣Lk?∣?
- ∣ D ∣ |D| ∣D∣(Dataset):数据集样本总数
- L(Label):标签,类别
给定特征的条件熵:含有 给定特征的所有特征值对应标签(输出)的信息熵之和,即
H
(
D
(
X
=
x
)
)
H(D_{(X=x)})
H(D(X=x)?)
H
(
D
∣
X
)
=
∑
x
P
(
x
)
H
(
D
∣
X
=
x
)
=
∑
i
=
1
n
∣
D
(
X
=
x
)
∣
∣
D
∣
H
(
D
(
X
=
x
)
)
=
?
∑
i
=
1
n
∣
D
(
X
=
x
)
∣
∣
D
∣
(
∑
k
=
1
K
∣
D
(
X
=
x
)
,
k
∣
∣
D
(
X
=
x
)
∣
log
?
2
∣
D
(
X
=
x
)
,
k
∣
∣
D
(
X
=
x
)
∣
)
\begin{aligned} H(D|X) &=\sum\limits_xP(x)H(D|X=x) \\ &=\sum\limits_{i=1}^n\frac{|D_{(X=x)}|}{|D|}H(D_{(X=x)}) \\ &=-\sum\limits_{i=1}^n\frac{|D_{(X=x)}|}{|D|}\bigg(\sum\limits_{k=1}^K\frac{|D_{(X=x),k}|}{|D_{(X=x)}|}\log_2\frac{|D_{(X=x),k}|}{|D_{(X=x)}|}\bigg) \end{aligned}
H(D∣X)?=x∑?P(x)H(D∣X=x)=i=1∑n?∣D∣∣D(X=x)?∣?H(D(X=x)?)=?i=1∑n?∣D∣∣D(X=x)?∣?(k=1∑K?∣D(X=x)?∣∣D(X=x),k?∣?log2?∣D(X=x)?∣∣D(X=x),k?∣?)?
- X X X某个特征
- x x x某个特征值
- ∣ D ( X = x ) ∣ |D_{(X=x)}| ∣D(X=x)?∣整个样本中取特征值 x x x的样本数量
- ∣ D ( X = x ) , k ∣ |D_{(X=x),k}| ∣D(X=x),k?∣整个样本的特征X取特征值 x x x时对应标签的样本数量
步骤
分情况
- 特殊情况1:所有瓜都是同1个label(输出类型),所有的瓜都是好瓜,返回1个label即可,返回“好瓜”,不管如何分类都是好瓜
- 特殊情况2:每1个特征的特征值都是相同的,所有的瓜各种特征的特征值都一样,通过特征值无法判断好瓜坏瓜,直接少数服从多数
- 一般情况:所有瓜有多个label(输出类型),有好瓜也有坏瓜;存在几个瓜的特征值有所不同
步骤
- 处理特殊情况1:任选1个label返回
- 处理特殊情况2:返回多数样本对应label
- 处理一般情况:
- 根节点:使用数据集计算每个特征的信息增益,返回最大增益的特征
- 树杈:将最大增益特征的特征值作为树杈
- 逐个获取树杈特征值所在行数据(去掉树杈特征值)+特征行(去掉树杈特征值所属特征) ,产生树杈子数据集
- 重复1,2,3,直到叶子结点
数据集
采用经典数据集
- 分类西瓜
- 提取码:d9rj
代码
from math import log2
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
def calculate_entropy(labels):
"""
计算信息熵
labels=
数据集信息熵:输出=Y=labels
特征信息熵:某个特征一类特征值对应labels
:param labels: 输出值
:return:
"""
# results-色泽特征:{‘是’:8,'否':9}
"""
total:labels长度
total=
数据集信息熵:输出包含样本数=Y包含样本数=labels长度
特征信息熵:此特征一类特征值包含样本数=labels长度
"""
total = len(labels)
# result={label1:对应样本数量,label2:对应样本数量},例子{‘是’:8,'否':9}
label_num = {}
for index_label in labels:
label_num[index_label[-1]] = label_num.get(index_label[-1], 0) + 1
"""
entropy(信息熵)=
数据集信息熵:sum(输出Y一类样本数量/输出Y样本总数)
特征信息熵:sum(此特征一类特征值样本数量/特征值样本总数)
"""
entropy = sum([-1.0 * num / total * log2(num / total) for num in label_num.values()])
return entropy
def calculate_feature_gain(fvalues, data):
"""
计算每个feature的信息增益
:param fvalues: 某个特征的特征值
:param data: 数据集
:return:
"""
# 特征值总数
total = len(fvalues)
# labels=data.iloc[:, -1]
# 根据特征值values分组labels,分组时会对values去重
# grouped_value_labless=((特征值1,((索引,label_m),(索引,label_n),...)),(特征值2,((索引,label_x),(索引,label_y),...)),...)
grouped_value_labless = data.iloc[:, -1].groupby(by=fvalues)
# 特征条件熵 含有 对应特征的所有特征值信息熵之和
# gf[1]取出 特征值 对应的 labels
condition_entropy = sum([(len(value_labels[1]) / total) * calculate_entropy(value_labels[1]) for value_labels in
list(grouped_value_labless)])
# 数据集信息熵=所有特征的信息熵之和
data_entropy = calculate_entropy(data.iloc[:, -1])
return data_entropy - condition_entropy
def get_max_info_gain(data):
"""
获取信息增益最大的特征
:param data: 数据集
:return: (feature,信息增益)
"""
# 计算每个特征的信息增益 [(feature1,信息增益),(feature2,信息增益)...]
feature_gains = [(feature, calculate_feature_gain(data[feature], data)) for feature in data.iloc[:, :-1]]
# 根据每个特征的信息增益倒序排序
feature_gains = sorted(feature_gains, key=lambda f: f[1], reverse=True)
# 返回信息增益最大的特征
return feature_gains[0]
def get_new_value_datas(data, best_feature):
"""
获取树杈特征值所在行数据(去掉树杈特征值)+特征行(去掉树杈特征值所属特征) ,产生树杈子数据集
:param data:
:param best_feature:
:return:
"""
values = pd.unique(data[best_feature])
# data[data[best_feature] == v]:取特征值相等的数据
# [('青绿',所有青绿data),('乌黑',所有乌黑data),('浅白',所有浅白data)]
value_datas = [(v, data[data[best_feature] == v]) for v in values]
# axis=1:列;vd[0]:特征值;vd[1]:data
# vd[1].drop([best_feature], axis=1)):丢弃最佳特征值所在列和行
new_value_datas = [(value_data[0], value_data[1].drop([best_feature], axis=1)) for value_data in value_datas]
return new_value_datas
def get_most_label(labels):
"""
出现最多的label
:param labels: 输出=Y=labels=Series((0,'是'),(1,'是')...)
:return:
"""
# 统计每个label出现的数量
label_num = {}
for label in labels:
# 0表示没有get到则返回0
label_num[label] = label_num.get(label, 0) + 1
# 根据label_num中的num倒序排序
sorted_label = sorted(label_num.items(), key=lambda ll: ll[1], reverse=True)
# 返回数量最多的label
return sorted_label[0][0]
def create_decision_tree(data, feature_values):
"""
创建决策树
:param data: 整个数据集
:param feature_values:
feature_value={'色泽': ['青绿', '乌黑', '浅白'], '根蒂': ['蜷缩', '稍蜷', '硬挺'], ...}
特征值已去重
:return: decision_tree
"""
# data.iloc[:, -1] :表示取所有行(不包括表头) -1表示取最后一列
# !输出=Y=labels=Series((0,'是'),(1,'是')...)
labels = data.iloc[:, -1]
# 特殊情况1:所有瓜都是同1个label,所有的瓜都是好瓜,返回1个label即可,返回“好瓜”,不管如何分类都是好瓜
if len(pd.unique(labels)) == 1:
return labels.values[0]
# 特殊情况2:每1个特征的特征值都是相同的,所有的瓜各种特征的特征值都一样,通过特征值无法判断好瓜坏瓜,直接少数服从多数
if all([len(pd.unique(data[feature])) == 1 for feature in data.iloc[:, :-1].columns]):
return get_most_label(labels)
# 一般情况:所有瓜有多个label,有好瓜也有坏瓜;存在几个瓜的特征值有所不同
# get_max_info_gain(data)返回值为(feature,信息增益)
best_feature = get_max_info_gain(data)[0]
decision_tree = {best_feature: {}}
# 特征值去重
bestfeature_original_values = feature_values[best_feature]
# feature_values 特征值已经去重
bestfeature_rest_values = pd.unique(data[best_feature])
# 下一个结点是叶子结点(label值):添加差集特征值到决策树中
# 原始数据最佳特征 特征值数量 != 剩余数据中最佳特征 特征值数量,将到叶子结点
if len(bestfeature_original_values) != len(bestfeature_rest_values):
# bestfeature_original_values中独有的values
no_exist_values = set(bestfeature_original_values) - set(bestfeature_rest_values)
for nev in no_exist_values:
# 结点(best_feature) 连线(特征值)叶子结点(label)
# 连线只有1条,特征值都相同
decision_tree[best_feature][nev] = get_most_label(labels)
# 下一个结点不是叶子结点(label值):利用特征值的子数据集 创建子决策树
# new_value_datas,value是best_feature的特征值们,data是value所在的行(去掉value)+特征行(去掉value所属特征)
# value_data[0]:特征值;value_data[1]:data
new_value_datas = get_new_value_datas(data, best_feature)
for value_data in new_value_datas:
decision_tree[best_feature][value_data[0]] = create_decision_tree(value_data[1], feature_values)
return decision_tree
if __name__ == '__main__':
data = pd.read_excel('./data/watermelon.xlsx')
# 最后一列是输出是Y=lable
# data.iloc[:, :-1].columns :表示所有行 :-1表示“第1列到倒数第2列” columns表示取列头
# pd.unique(data[feature])表示唯一化特征feature的特征值
# !feature_values={'色泽': ['青绿', '乌黑', '浅白'], '根蒂': ['蜷缩', '稍蜷', '硬挺'], ...}
feature_values = dict([(feature, list(pd.unique(data[feature]))) for feature in data.iloc[:, :-1].columns])
decision_tree = create_decision_tree(data, feature_values)
print(decision_tree)
结果
json
{
"色泽": {
"青绿": {
"根蒂": {
"蜷缩": {
"敲声": {
"清脆": "是 ",
"浊响": "是 ",
"沉闷": {
"纹理": {
"模糊": "是 ",
"清晰": "是 ",
"稍糊": "否 "
}
}
}
},
"稍蜷": {
"敲声": {
"清脆": "是 ",
"沉闷": "是 ",
"浊响": {
"纹理": {
"模糊": "是 ",
"清晰": "是 ",
"稍糊": "否 "
}
}
}
},
"硬挺": "否 "
}
},
"乌黑": {
"根蒂": {
"硬挺": "是 ",
"蜷缩": "是 ",
"稍蜷": {
"敲声": {
"清脆": "是 ",
"浊响": {
"纹理": {
"模糊": "是 ",
"稍糊": "是 ",
"清晰": {
"脐部": {
"平坦": "是 ",
"凹陷": "是 ",
"稍凹": {
"触感": {
"硬滑": "是 ",
"软粘": "否 "
}
}
}
}
}
},
"沉闷": "否 "
}
}
}
},
"浅白": {
"根蒂": {
"蜷缩": {
"敲声": {
"清脆": "否 ",
"沉闷": "否 ",
"浊响": {
"纹理": {
"稍糊": "否 ",
"清晰": "是 ",
"模糊": "否 "
}
}
}
},
"硬挺": "否 ",
"稍蜷": "否 "
}
}
}
}