Article
文献题目:Multi-hop reasoning over paths in temporal knowledge graphs using reinforcement learning
文献时间:2021
发表期刊:Applied Soft Computing
摘要
- 知识图谱(KGs)通常是不完整的——许多新的事实可以从 KGs 和现有的信息中推断出来。在一些传统的推理方法中,没有考虑时间信息,这意味着只训练三元组(头、关系、尾)。在当前的动态知识图中,考虑事实的时间方面是一个挑战。最近的时间推理方法将时间信息嵌入到低维空间中。这些方法主要支持隐式推理,即无法得到具体的推理路径。这些方法限制了推理路径的准确性,并忽略了时间知识图(TKG)中多个可解释的推理路径。为了克服这个限制,我们在本文中提出了一种多跳推理模型 TPath。它是一种强化学习(RL)框架,可以学习多跳推理路径并不断调整 TKG 中的推理路径。更重要的是,我们在推理路径中添加了时间向量,进一步提高了推理路径的准确性。同时,考虑到时间推理路径的多样性,我们提出了一个新的奖励函数。在 TPath 中,代理使用长短期记忆网络 (LSTM) 从环境中捕获当前观察结果,并通过激活函数将动作向量(关系向量和时间向量)输出到环境。在实验上,我们的模型在两个公共时间知识图数据集的几个方面优于其他最先进的推理方法。
引言
- 知识图谱是人工智能中的一个重要概念,在问答[1]、社交网络[2]、语义解析[3]等许多应用中发挥着重要作用。表示为三元组(头部、关系、尾部)的关系事实的集合,例如(Donald Trump、Consult、Vladimir Putin)。尽管知识边图由大量的三元组组成,但它们还远未完成。在推理任务中,通过观察到的信息来推断事实(不直接存储在知识图中)是一个很大的挑战。从早期开始,推理方法 [4-6] 将三元组的实体和关系嵌入到低维向量空间中,并通过评分函数对推理向量进行评分。同时,这些方法主要支持隐式推理,忽略了可解释的推理路径,限制了它们在更复杂的推理任务中的使用。杨等人 [7] 提出了一种新颖的模型,该模型学习逻辑规则并训练固定长度的可解释推理路径。一些推理方法[8-10]考虑了强化学习框架,进一步学习了KGs中的多跳推理路径。然而,大量的事件数据包含复杂的时间信息,传统的推理方法很难以三元组的形式学习时间信息。知识图谱需要扩展到表示为 4 元组 ( e s , r , e o , t i m ) (e_s, r, e_o, tim) (es?,r,eo?,tim) 的时间知识图谱 (TKG)。它是观察到的信息,每条边表示两个实体在该时间点通过关系连接。
- 最近,时间知识图谱推理逐渐受到关注。一些研究人员 [11-13] 将嵌入技术应用于 TKG,将时间信息表达嵌入到低维空间中。然而,他们忽略了事件随时间的动态变化。一些推理方法 [14-16] 考虑事实的时间范围来学习复杂事件。另一个类似的工作是时间感知进展:Jiang et al[17] 通过使用事实之间的时间顺序信息提出了一种时间感知的 KG 嵌入模型。韩等人 [18]利用深度学习架构来捕获时间依赖性。它们仅在不同实体的隐式推理边缘进行推理,不能处理特定的推理路径。隐式推理路径是指模型只能得到最终的推理结果,而不能推理出真实的、具体的推理路径。具体的推理路径意味着我们的模型可以得到所有的推理路径,包括头部实体、关系、尾部实体和时间信息。
- 在图 1 所示的知识图中,给定未观察到的事实
(
D
o
n
a
l
d
T
r
u
m
p
,
C
o
n
s
u
l
t
,
?
)
(Donald Trump, Consult, ?)
(DonaldTrump,Consult,?),有两个结果:“Elizabeth II”和“Vladimir Putin”。我们不能直接得到一个精确的目标实体,这会导致推理的准确性下降。然而,在时间知识图谱中,给定未观察到的事实
(
D
o
n
a
l
d
T
r
u
m
p
,
C
o
n
s
u
l
t
,
?
,
2018
?
10
?
11
)
(Donald Trump, Consult, ?, 2018-10-11)
(DonaldTrump,Consult,?,2018?10?11),我们可以很容易地在时间知识图谱推理中得到准确的答案“伊丽莎白二世”。对于时序知识图推理任务,目前的方法主要支持隐式推理路径(无法得到具体的推理路径)。例如,给定未观察到的事实
(
D
o
n
a
l
d
T
r
u
m
p
,
S
i
g
n
f
o
r
m
a
l
a
g
r
e
e
m
e
n
t
,
?
,
2019
?
05
?
07
)
(Donald Trump,Sign formal agreement,?,2019-05-07)
(DonaldTrump,Signformalagreement,?,2019?05?07),当前的方法只返回一个不确定的结果(可能是正确的结果或不正确的结果),它会限制推理的准确性时间知识图谱。在我们的模型中,我们可以从以下时间特定的多跳推理路径推断出未观察到的事实(Donald Trump,Sign formal agreement,?,2019-05-07):Donald Trump→Consult/2018-10 24→Vladimir Putin→Make optimistic comment/2018-10-29→United States→Host a visit//2018-11-05→China。这意味着我们的模型可以获得特定的多跳推理路径,并提高时间知识图谱中推理的准确性。

- 图 1. 时间知识图的一小部分。 实线箭头表示观察到的和存在的关系,TKG 中的时间链接和虚线箭头表示推理路径中的关系和时间信息。 r ? 1 r^{-1} r?1 表示关系 r r r 的倒数。 请注意,可以通过推理起始实体 Donald Trump 和相应目标实体之间的路径来推理粗体关系。
- 在本文中,我们为复杂的时间知识图提出了一种新颖的多跳推理模型。首先,我们通过强化学习(RL)框架对路径推理过程进行建模。更重要的是,我们将时间信息添加为一个单独的向量,参与环境和代理的迭代。更重要的是,我们提出了一个策略网络,可以训练代理学习时间多跳推理路径。此外,我们提出了一种新颖的奖励函数,该函数在处理时间知识图推理的多样性方面具有良好的性能。在时间知识图中,给定一个缺失的 4 元组 ( e n t i t y 1 , r e l a t i o n , ? , t i m e ) (entity1, relation, ?, time) (entity1,relation,?,time),代理学习策略网络,该网络可以通过从实体 1 中选择每一步的动作来学习到达目标实体。同时,agent会通过reward函数调整整条路径。我们将模型 TPath 称为“时间多跳推理路径”。我们在两个基准数据集上评估 TPath,实验结果在几个方面与最先进的模型相比显示出显着且一致的改进。同时,这些结果也意味着多跳路径可以适用于时间知识图,并且我们的模型可以扩展到大型时间知识图。
- 本文的主要贡献:
- 我们提出了一种在时间知识图中使用强化学习框架的新型时间推理模型。
- 我们构建了一个新的策略网络,它考虑了时间向量,并在时间知识图中选择了特定的多跳推理路径。
- 我们提出了一种新的奖励函数,它考虑了时间推理路径的多样性,并在整个时间多跳路径中提供了更好的控制。
- 实验表明,我们的模型可以扩展到大型时间知识图,在几个方面优于一些最先进的推理方法。
- 本文的其余部分安排如下。 第 2 节简要介绍了相关工作。 我们在第 3 节中提出了我们的模型并详细说明了它的训练过程。第 4 节给出了实验评估。第 5 节总结了本文。
相关工作
传统知识图谱推理
- 嵌入技术作为传统知识图谱推理的主要技术,得到了广泛的研究。 Bordes 等人[4] 提出 TransE,将实体和关系嵌入到相同的低维向量空间中,并为每个事实定义一个评分函数来衡量其准确性。由于 TransE 在建模 1 对 N、N 对 -1 和 N 对 N 关系时存在问题,因此提出了 TransH [5] 以使实体在涉及各种关系时具有不同的表示。接下来,Lin 等人 [6] 提出了实体和关系在单独的实体空间和关系空间中的嵌入方法,它通过投影实体之间的翻译来学习嵌入。 Yang等人[19]将关系矩阵约束为对角矩阵以降低计算成本。还有其他改进的模型考虑了额外的信息,如异质性 [20]、神经网络 [21] 和张量分解 [22]。 Wang 等人 [23] 对这些模型进行了全面的回顾。然而,这些方法无法在知识图谱中得到具体且可解释的推理路径。 Yang 等人 [7] 提出了 NeuralLP,它在端到端可微模型中学习一阶逻辑规则,以解决知识库推理中学习概率一阶逻辑规则的问题。此外,Xiong 等人 [8] 考虑了用于学习知识图中关系路径的强化学习 (RL) 框架。 Das 等人 [9] 探索了一种在大型知识库上进行自动推理的新方法,该方法训练代理根据输入查询走到答案节点。它解决了更困难和更实际的任务,即在关系已知但只有一个实体的情况下回答问题。然而,这些方法会收到错误的否定监督,并偶然导致正确的推理路径。 Lin 等人 [24] 采用预训练的一跳嵌入模型来准确表示环境并对抗虚假路径来探索搜索空间。 Wang 等人 [25] 探索了一种称为 AttnPath 的强化学习新机制,它结合了长短期记忆网络和图注意机制,以减轻模型的预训练。 Hildebrandt 等人 [10] 提出了使用辩论动力学来揭示关系,这是一种基于两个对立强化学习代理之间辩论的知识图推理方法。然而,他们没有考虑时间知识图中的动态复杂时间变化。我们可以在表 1 中总结传统知识图推理模型的特性。我们的模型 TPath 考虑了时间信息,我们提出了一种新的策略网络来训练时间知识图中的多个可解释推理路径。

时间知识图推理
- 在时间 RDF(资源描述框架)领域,Gutiérrez 等人 [26] 提出了时间 RDF 的定义,并证明时间图的蕴涵不会比 RDF 蕴涵产生额外的复杂性。 Pugliese 等人 [27] 提出了归一化时间 RDF 图的概念,并提出了基于 SPARQL 的这些图的查询语言。 Zimmermann 等人[28] 提出了一个通用框架,用于使用带注释的语义 Web 数据表示和推理,以及用于时间 RDF 模式子集的非近似推理算法。
- 随着知识图谱越来越流行,许多研究人员将研究重点从时间 RDF 转移到时间知识图谱上。最近有一些处理 TKG 中时间信息的方法。 Dasgupta 等人 [11] 提出了 HyTE,它通过将每个时间戳与相应的超平面相关联,明确地将时间纳入实体关系空间。它在时间上利用 KG 的范围事实来执行 KG 推理,并且还可以预测未注释时间事实的时间范围。同年,García-Durán 等人 [13] 利用循环神经网络通过结合时间信息来学习关系类型的时间感知表示。 Leblay 等人[12] 将时间信息嵌入到低维空间中。这些方法都是基于嵌入技术,无法捕捉时间依赖性。接下来,Trivedi 等人 [14] 提出了 Know-Evolve,这是一种新颖的深度进化知识网络,它随着时间的推移学习非线性进化的实体表示。 Ma 等人[16] 将传统知识图(即 ComplEx、DistMult)的领先方法推广到时间知识边缘图,并提出了一种新的张量模型,称为 ConT,这是一种存储情景数据的有效方法,并且能够概括到新的事实。此外,Jin 等人 [15] 在 Know-Evolve 中发现了一个有问题的公式,并提出了一种新的神经架构来建模复杂的事件序列。另一个密切的工作是时间电子意识的进步。姜等人[17]使用现有事实和事实的时间信息来预测 TKG 中的链接。 Han 等人 [18] 提出了 Graph Hawkes 神经网络,这是一种深度学习架构,用于捕获对时间知识图的时间依赖性。我们可以总结表2中时间知识图推理模型的属性。我们的模型TPath可以选择多个特定的时间推理路径,进一步提高推理路径的准确性。

模型
- 在本节中,我们将详细提出我们的模型。 首先,我们介绍了环境和针对代理的策略网络。 代理通过与环境交互来学习选择最佳推理路径。 然后,我们将介绍 TPath 的训练过程以及环境和代理之间的交互算法。 我们的整体模型如图 2 所示。
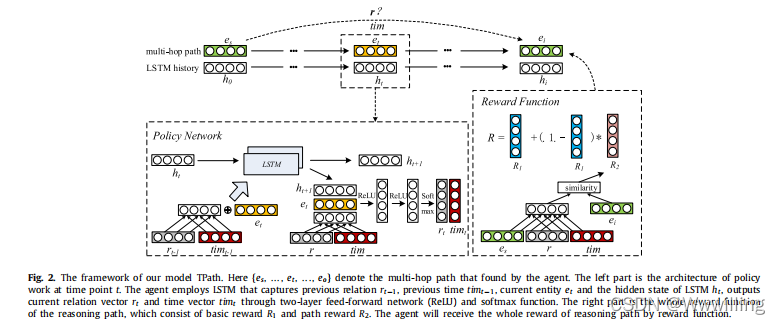
- Fig2:我们模型 TPath 的框架。 这里 { e s , . . . , e t , . . . , e o } \{e_s , . . . , e_t, . . . , e_o\} {es?,...,et?,...,eo?} 表示代理找到的多跳路径。 左边部分是时间点 t t t 的策略工作架构。 代理采用 LSTM 捕获先前关系 r t ? 1 r_{t-1} rt?1?、先前时间 t i m t ? 1 {tim}_{t-1} timt?1?、当前实体 e t e_t et? 和 LSTM h t h_t ht? 的隐藏状态,通过两层前馈网络 (ReLU) 输出当前关系向量 r t r_t rt? 和时间向量 t i m t {tim}_t timt? 和 softmax 函数。 右边是推理路径的整个奖励函数,由基本奖励 R 1 R_1 R1?和路径奖励 R 2 R_2 R2?组成。 代理将通过奖励函数获得推理路径的全部奖励。
推理路径的强化学习
- 我们的强化学习框架分为两部分。 在第一部分中,我们将把环境介绍为时间知识图上的部分观察马尔可夫决策过程(POMDP)。 我们定义一个 5 元组 ( S , O , A , P , R ) (S, O, A, P, R) (S,O,A,P,R) 来表示 POMDP,其中 S S S 是有效的连续状态空间, O O O 是未观察到的完整状态空间, A A A 是所有可能动作的集合, P P P 是 转移概率矩阵(区别于图中的符号 T T T), R R R是从状态空间采取行动的奖励函数。 在第二部分,我们将介绍策略网络 π θ π_θ πθ?,它从给定的缺失 4 元组 ( e s , r , ? , t i m ) (e_s,r,?,tim) (es?,r,?,tim)中推断出目标实体。 从实体开始,代理学习寻找目标实体 e o e_o eo?。 然后,代理将在到达目标实体时停留在目标实体上。 同时,环境将返回推理路径的全部奖励。
- 我们正式定义了 TKG 中的多关系和多跳推理任务。 TKG 是存储为 4 元组 ( e s , r , e o , t i m ) (e_s, r, e_o, tim) (es?,r,eo?,tim) 的事实的集合, e s , e o ∈ ? , r ∈ R , t i m ∈ T e_s, e_o ∈ ?, r∈R, tim∈T es?,eo?∈?,r∈R,tim∈T,其中 ? ? ? 表示实体集, R R R 和 T T T 是二元关系和时间点的集合。 我们的模型对表单的目标实体 ( e s , r , ? , t i m ) (e_s,r,?,tim) (es?,r,?,tim)进行推理,例如 ( D o n a l d T r u m p , S i g n f o r m a l a g r e e m e n t , ? , 2019 ? 05 ? 07 ) (Donald Trump, Sign formal agreement, ?, 2019-05-07) (DonaldTrump,Signformalagreement,?,2019?05?07)。它还返回整个奖励以预测事实是否属实,例如 ( D o n a l d T r u m p , S i g n f o r m a l a g r e e m e n t , C h i n a , 2018 ? 12 ? 04 ) ? (Donald Trump, Sign formal agreement, China, 2018-12-04)? (DonaldTrump,Signformalagreement,China,2018?12?04)?
环境
- 我们的环境是一个 POMDP。 形式上,TKG 是一个有向和标记的多图 G = ( V , E , R , T ) G = (V, E, R, T) G=(V,E,R,T),其中 V V V 和 E E E 分别表示图的顶点和边。 注意 V = ? V = ? V=? 和 E ? V × R × V × T E?V×R×V×T E?V×R×V×T。 因此,我们将 POMDP 定义为 5 元组 ( S , O , A , P , R ) (S,O,A,P,R) (S,O,A,P,R),其中 POMDP 的每个组件如下所示。
- S S S(状态)。 状态空间 S S S,每个状态 s ∈ S s∈S s∈S用 s = ( e t , e s , r , e o , t i m ) s = (e_t, e_s, r, e_o, tim) s=(et?,es?,r,eo?,tim)表示,其中 e t e_t et?是当前实体, e s e_s es?和 e o e_o eo?分别是起始实体和目标实体, r r r表示 e s e_s es? 和 e o e_o eo? 在时间 t i m tim tim之间的关系。 S S S 由所有观察到的和有效的组合组成。
- O O O(观察)。 环境是不可观察的,只转移它的当前位置和任务,即 ( e t , e s , r , t i m ) (e_t,e_s,r,tim) (et?,es?,r,tim)被观察到。 观测函数 O : S → V × V × R × T O:S→V×V×R×T O:S→V×V×R×T定义为 O ( s = ( e t , e s , r , e o , t i m ) ) = ( e t , e s , r , t i m ) O(s = (e_t, e_s, r, e_o, tim)) = (e_t, e_s, r, tim) O(s=(et?,es?,r,eo?,tim))=(et?,es?,r,tim)。
- A A A(行动)。 动作空间被定义为来自状态 s s s 的一组可能关系和时间点,该状态 s s s 由 G G G 中顶点 e t e_t et? 的所有出边组成,即 A s = { ( r , t i m ∣ s ) } A_s = \{(r, tim|s)\} As?={(r,tim∣s)}。 形式上, A = { ( e t , r c , v , t i m c ) ∈ E : s = ( e t , e s , r , e o , t i m ) , r c ∈ R , v ∈ V , t i m c ∈ T } A = \{ (e_t, r_c , v, {tim}_c ) ∈E: s = (e_t, e_s, r, e_o, tim), r_c ∈R, v∈V, {tim}_c ∈T \} A={(et?,rc?,v,timc?)∈E:s=(et?,es?,r,eo?,tim),rc?∈R,v∈V,timc?∈T},其中 v v v 是临时实体 。这意味着每个状态的代理在时间 t i m c {tim}_c timc? 从多个选项中选择出边 r c r_c rc? 并到达临时顶点 v v v。同时,代理采取的推理路径步骤少于给定长度。 为了使代理在给定的步数内停留在目标节点,将一个特殊的自循环动作添加到从节点到自身的动作空间中。
- P P P(转换)。 环境通过代理选择的边将状态更新为新的状态顶点。 形式上,转移函数是 P : S × R × T × V → S P:S×R×T×V→S P:S×R×T×V→S 定义为 P ( s , a ) = ( v , e s , r , e o , t i m ) P(s, a) = (v, e_s, r, e_o, tim) P(s,a)=(v,es?,r,eo?,tim),其中 s s s 是状态, a a a 是代理选择的动作空间。
- R R R(奖励)。 有两个因素会影响时间推理路径的质量,如下所示。
- 基本奖励:在我们的环境中,代理需要从大量动作中选择特定动作。 我们将基本奖励函数定义如下,以指导代理做出选择,使其能够到达目标实体
e
o
e_o
eo?。

- 路径奖励:在时间推理路径中,代理倾向于选择重复的有效路径,这将限制推理路径的范围。== 为了确定当前实体在推理路径中的位置并鼓励代理尽可能探索积极的路径==,我们定义了考虑重复推理路径的第二个奖励函数,如下所示:
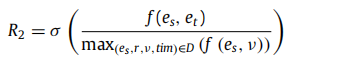
- 其中 σ ( x ) σ(x) σ(x) 是 sigmoid 函数, D D D 表示时间知识图中所有真实且观察到的 4 元组 ( e s , r , v , t i m ) (e_s, r, v, tim) (es?,r,v,tim), f ( x , y ) f (x, y) f(x,y) 表示从实体 x x x 到当前实体 y y y 的推理路径,通常是实体之间的点积。 路径奖励对推理路径进行打分,会适当降低推理路径的整体奖励,进一步提升探索新实体的概率。
- 奖励:奖励是定义的奖励函数的线性组合。
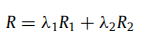
- 其中 R 1 R_1 R1? 和 R 2 R_2 R2? 在 Eq(1) 和 Eq(2) 中定义,线性参数 λ 1 , λ 2 ∈ [ 0 , 1 ] λ_1, λ_2∈ [0, 1] λ1?,λ2?∈[0,1]。
策略网络
- 时间知识图中有大量的实体、关系和时间点。 每个实体通常通过不同的边连接多个实体。 此外,两个实体之间存在多跳推理路径。 在一个时间知识图中,给定 ( e s , r , e o , t i m ) (e_s,r,e_o,tim) (es?,r,eo?,tim),我们在实体对 ( e s , e o ) (e_s,e_o) (es?,eo?)之间定义了多个推理路径: P = { p 1 , p 2 , . . , p m } P = \{p_1,p_2, . . , p_m\} P={p1?,p2?,..,pm?}, 其中 P ∈ ? m , p = { e s , r 0 : t i m 0 , e 1 , R 1 : t i m 1 , . . . , r k ? 1 : t i m k ? 1 , e o } , p ∈ P P ∈ ?^m, p = \{e_s, r_0:{tim}_0, e_1, R_1:{tim}_1, . . . , r_{k?1}:{tim}_{k?1}, e_o\}, p ∈P P∈?m,p={es?,r0?:tim0?,e1?,R1?:tim1?,...,rk?1?:timk?1?,eo?},p∈P , ‘:’ 表示向量连接。 推理路径的长度一般不超过6(≤6)。
- 基于长短期记忆 (LSTM) 的代理将历史
H
t
H_t
Ht? 编码为连续向量
h
t
∈
?
2
d
h_t ∈ ?^{2d}
ht?∈?2d。 历史
H
t
=
(
A
t
?
1
,
O
t
,
H
t
?
1
)
=
(
r
t
?
1
:
t
i
m
t
?
1
,
O
t
,
H
t
?
1
)
H_t = (A_{t-1}, O_t, H_{t-1}) = (r_{t-1}: {tim}_{t-1}, O_t, H_{t-1})
Ht?=(At?1?,Ot?,Ht?1?)=(rt?1?:timt?1?,Ot?,Ht?1?) 是过去行动和观察的序列。 我们还定义了
e
∈
?
∣
ε
∣
×
d
,
t
i
m
∈
?
∣
T
∣
×
d
e∈ ?^{|ε|×d},tim∈ ?^{|T |×d}
e∈?∣ε∣×d,tim∈?∣T∣×d 和
r
∈
?
∣
R
∣
×
d
r∈ ?^{|R|×d}
r∈?∣R∣×d 作为实体和二元关系的嵌入矩阵。 更新 LSTM 动力学如下:
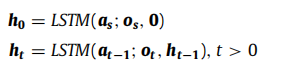
- 其中 A s A_s As? 表示来自起始实体 e s e_s es? 的特殊虚拟动作向量, o s o_s os? 是起始观察值, a t ? 1 = ( r t ? 1 , t i m t ? 1 ) a_{t-1} = (r_{t-1}, {tim}_{t-1}) at?1?=(rt?1?,timt?1?) 表示在时间 t-1 的关系和事件时间的向量表示, O t O_t Ot? 表示 在时间 t t t 的观察结果,’;’ 表示向量连接。
- 基于当前观察
O
t
O_t
Ot? 和当前历史向量
h
t
h_t
ht? ,网络选择关系和事件时间(动作)作为所有条件动作的输出。 神经网络是两层前馈网络,每一层后面都有一个整流非线性层(ReLU)。 输出是来自当前实体上所有可能的动作向量的动作向量,并使用 softmax 函数进行归一化。 策略网络
π
π
π 定义如下:
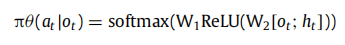
- 其中 W 1 W_1 W1? 和 W 2 W_2 W2? 是两层前馈神经网络的权重矩阵, O t O_t Ot? 和 H t H_t Ht? 是时间 t t t 的观察向量和历史向量,“;”表示向量连接。
训练
- 图 3 显示了通过环境和代理进行迭代指导的训练过程。 环境存储所有向量,包括实体向量、关系向量、时间向量等。给定一个缺失的 4 元组
(
e
,
r
,
?
,
t
i
m
)
(e, r, ?, tim)
(e,r,?,tim),用当前向量初始化状态
S
1
S_1
S1?,并将通过观察函数获得的观察
O
1
O_1
O1? 传输给代理。 代理将通过策略网络(图 2)计算动作
A
1
A_1
A1? 并将动作
A
1
A_1
A1? 传输到环境。 通过环境中的动作
A
1
A_1
A1? 从状态
S
1
S_1
S1? 转换为
S
2
S_2
S2? 后,代理将返回此推理路径的奖励(由公式
R
=
λ
1
R
1
+
λ
2
R
2
R = λ_1R_1 + λ_2R_2
R=λ1?R1?+λ2?R2?计算)。 这与环境和代理形成了迭代。 最后,训练过程将通过方程(7)和(8)得到整个推理路径的奖励,如下所示。
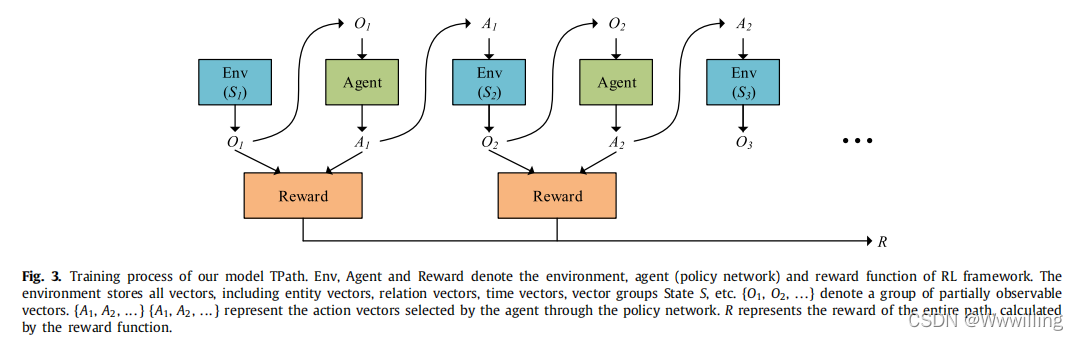
- 图 3. 我们的模型 TPath 的训练过程。 Env、Agent 和 Reward 表示 RL 框架的环境、代理(策略网络)和奖励功能。 环境存储所有向量,包括实体向量、关系向量、时间向量、向量组State
S
S
S等。
{
O
1
,
O
2
,
.
.
.
}
\{O_1, O_2, . . . \}
{O1?,O2?,...} 表示一组部分可观察的向量。
{
A
1
,
A
2
,
.
.
.
}
\{A_1, A_2, . . . \}
{A1?,A2?,...} 表示代理通过策略网络选择的动作向量。
R
R
R 表示整条路径的奖励,由奖励函数计算得出。
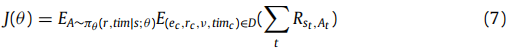
- 其中 J ( θ ) J(θ) J(θ) 表示一个情节的奖励, A A A 表示动作空间,第一个 E E E(期望)被替换为训练数据集的经验平均值。 对于第二个 E E E(期望值),我们通过为每个训练示例运行多个 rollout 来近似它。 D D D 表示时间知识图中所有真实的和观察到的 4 元组 ( e t , r c , v , t i m c ) (e_t, r_c , v, {tim}_c ) (et?,rc?,v,timc?), R S t , A t R_{S_t ,A_t} RSt?,At?? 表示在时间 t t t 在状态 S S S 中采取行动 A A A 的全部奖励。
- 用于更新策略网络的近似梯度为:
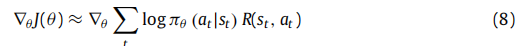
- 训练过程的细节在算法1中描述。首先,我们输入时间知识图的4元组向量
(
e
s
,
r
,
?
,
t
i
m
)
(e_s, r, ?, tim)
(es?,r,?,tim),包括实体向量、关系向量和时间向量。接下来,TPath 的训练过程是代理和环境之间的迭代(第 01-13 行)。对于每一集(第 01 行),我们初始化状态向量和剧集长度(第 02-03 行)。接下来,我们通过当前状态向量(第 04 行)得到观察向量。我们将先前的历史
h
t
?
1
h_{t-1}
ht?1? 和先前的动作设置在-1(第 05 行)。然后,我们使用上限 max_length(第 06 行)限制剧集长度。在推理路径 max_length 的长度内,代理将训练策略网络并获得下一个动作向量(第 07-08 行)。环境将到达下一个状态,并通过奖励函数计算推理路径的奖励给代理(第 09 行)。代理将通过当前状态更新观察向量(第 10 行),并增加步骤以在 max_length 内循环(第 11 行)。代理将更新参数 θ(第 12-13 行),算法最终会输出整个路径并最大化预期的累积奖励。

实验
实验设置
数据集
- 我们在两个事件数据集上评估我们的模型:全球事件、语言和音调数据库 (GDELT) [30] 和综合危机预警系统 (ICEWS) [31]。 同时,GDELT 数据集是从 2018 年 1 月 1 日到 2018 年 1 月 15 日收集的。ICEWS 数据集是从 2018 年 10 月 7 日到 2019 年 6 月 25 日收集的。两个数据集都包含包含两个实体、一个关系和一个时间点的事件记录。 表 3 报告了数据集的各种统计数据。 #Ent、#Rel 和#Time 表示实体、关系和时间点的数量。 此外,原始数据集按(80%)/(10%)/(10%)随机分为训练数据集、测试数据集和有效数据集。
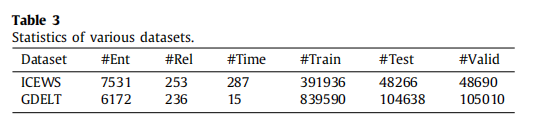
- 对于每个数据集,我们构建“图形”,在训练数据集中添加逆 4 元组。 例如train dataset中有一个4元组 ( e 1 , r , e 2 , t i m ) (e_1, r, e_2, tim) (e1?,r,e2?,tim),它的逆4元组是 ( e 2 , r ? 1 , e 1 , t i m ) (e_2, r^{?1}, e_1, tim) (e2?,r?1,e1?,tim),其中 r ? 1 r^{?1} r?1表示 r r r的逆关系 . 在训练过程中,代理可以通过 TKG 中的逆 4 元组返回。
- 为了评估推理路径的性能,我们分别对两个原始数据集中的关系进行排名,并构建 top-n 关系的子集作为推理任务。 对于每个前 n n n 个关系 r n r_n rn?,我们从原始数据集中提取所有具有 r n r_n rn? 的 4 元组,并将它们拆分为关系 r n r_n rn? 的训练、有效、测试数据集。 此外,我们生成了一些错误的 4 元组,并使用测试数据集对它们进行排序,以评估推理任务。
基线方法
- 我们用一些推理方法评估我们的模型:(1)传统知识图推理。 我们总结了一些通过忽略时间点来训练事件数据集的常见推理模型,例如 TransE [4]、NeuralLP [7]、DistMult [19] 和 MINERVA [9]。 (2)时序知识图推理。 我们还使用最先进的时间推理模型对时间知识图进行评估,包括 TTransE [12] 和 TA-TransE/DisMult [13]。
实验细节
- 我们添加每个关系的逆关系,即对于每个 4 元组 ( e s , r , e o , t i m ) (e_s, r, e_o, tim) (es?,r,eo?,tim),我们将 ( e o , r ? 1 , e s , t i m ) (e_o, r^{?1}, e_s, tim) (eo?,r?1,es?,tim) 附加到图中。 使用这些逆元组,代理可以返回到先前的实体并撤消 TKG 中的错误决定。
- 我们将嵌入维度大小设置为 50。动作嵌入是通过连接实体向量和关系向量形成的。 我们使用维度大小为 200 的一层 LSTM。MLP 的隐藏层大小(权重 W 1 W_1 W1? 和 W 2 W_2 W2?)设置为 200。我们使用 Adam Optimizer [32] 作为具有默认超参数设置的随机优化器:我们将 β β β 设置为 {0.05} 的范围和 λ λ λ 在 {0.02, 0.10, 0.15} 的范围内,其中 β β β 是熵正则化常数, λ λ λ 是 REINFORCE 基线的移动平均常数。
- 对于实验,我们设置最大长度 T = 3 T = 3 T=3。按照惯例,我们使用平均倒数排名(正确答案排名的倒数之和)、平均精度(MAP)和 Hits@1/3/10( 正确答案在前 1/3/10 结果中的案例百分比)作为评估指标。
评估协议
性能比较
- 表 4 通过两个公共数据集的基线总结了我们模型的性能:ICEWS 和 GDELT。 上部分介绍了传统的知识图谱推理方法,下部分介绍了时间知识图谱推理方法。
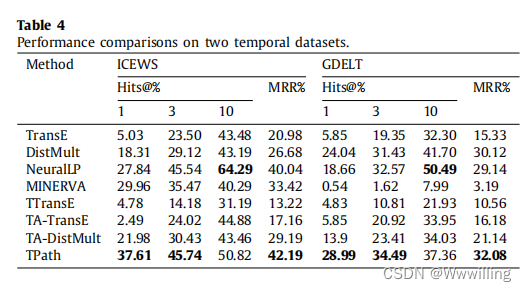
- 我们发现我们的模型 TPath 优于除 NeuralLP 之外的其他传统知识边图推理方法(Hits@10:ICEWS 上为 64.29% 对 50.82,GDELT 上为 50.49% 对 37.36%)。我们发现,在传统知识图推理中忽略时间信息后,数据集有大量相同的三元组,这使得它们易于学习。同时,NeuralLP 不受逻辑规则长度的限制,比我们的模型(推理路径的固定长度)更具适应性。 TPath 在两个数据集上比 MINERVA 方法表现出色。特别是对于 GDELT,我们的结果总体上提高了 30%。这意味着时间信息将帮助代理在多跳路径中到达目标实体。结果表明,考虑时间信息在时间推理中是有效的。接下来,在底部,我们发现 TPath 在两个数据集上优于所有其他时间知识图推理方法。我们的结果在 ICEWS 和 GDELT 上总体增加了 5.94% 和 3.33%。 TTransE、TA-TransE 和 TA-DistMult 主要支持对隐式推理路径的推理,这些结果意味着多跳路径可以适用于时间知识图谱。
时间推理路径分析
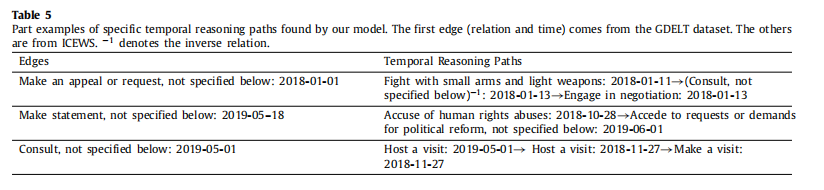
- 为了分析时间推理路径,我们在表 5 中分别展示了由 TPath 找到的一些特定推理路径。边表示两个实体在某个时间通过关系链接。 时间推理路径表示由我们的模型训练的特定时间推理路径。 同时,我们以第一条边“Make an appeal or request, not specified below:2018-01-01”为例。 在 TKG 中未观察到“2019-05-18”时间的“Make statement, not specified below”关系。 该模型将在观察到的 TKG 中选择时间推理路径。 具体时序推理路径之一如下所示:‘Fight with small arms and light weapons: 2018-01-11’→‘(Consult, not specified below)?1: 2018-01-13’→‘Engage in negotiation: 2018-01-13’。 这意味着我们的模型可以获得特定的时间推理路径,而不是隐式推理向量。
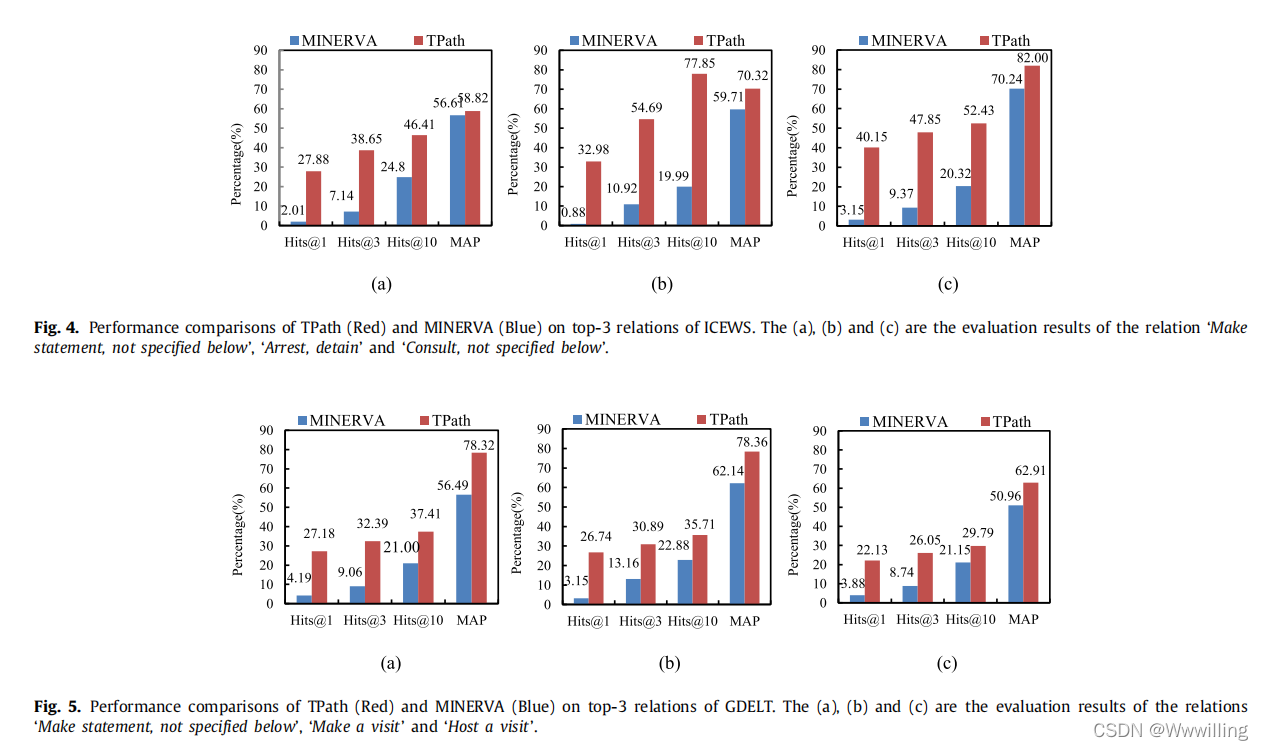
- 此外,我们分别提取 top-3 关系并构建两个数据集的特殊关系子集。 在 ICEWS 中,我们分别提取了具有 top-3 关系的 4 元组:“Make statement, not specified below”、“Arrest, detain”和“Consult, not specified below”。 此外,我们从测试数据集中生成负例,并用正例对它们进行排序。 为了公平比较,我们在实验中使用相同的排名文本。
- 对于这个实验,我们将路径长度设置为 3,迭代次数设置为 100。我们比较了每个推理任务的 Hits@1、Hits@3、Hits@10 和平均精度 (MAP) 分数。 图 4 和图 5 分别总结了我们的模型在 ICEWS 和 GDELT 上使用 MINERVA 的性能结果。 对于整体 Hits@1/3/10 和 MAP,如图 2 所示。 如图 4 和 5 所示,我们的模型明显优于 MINERVA 方法,这验证了 TKG 的强大推理能力。 在无花果。 在图 4 和 5 中,我们可以看到:(1) 我们的结果在 Hits@1/3/10 上总体平均增长了 25%。 这表明我们的模型可以提高特殊关系数据集中推理路径的性能。 (2) TPath 在 MAP 上优于基线方法。 这意味着时间信息在多跳路径中起着至关重要的作用。 由于 MINERVA 未能在推理路径中使用时间信息,因此它的性能通常比我们的模型差。
- 我们的模型可以训练不同长度的推理路径。 为了评估不同长度对实验结果的性能,我们检查了各种长度的有效性。 图 6 显示了我们的模型在两个数据集上在不同长度的推理路径下的性能。 从图 6 中,我们观察到:(1)当时间推理路径的长度为 3 时,结果显着优于我们模型中其他时间推理路径的长度。(2)当时间推理路径的长度为 2 时 ,结果没有达到预期的性能(不是0)。 我们发现两个数据集中的实体之间没有足够的时间推理路径(路径长度:2),我们的模型很难达到预期的结果。 (3)当路径长度为4到6时,我们分别对每个长度进行训练,结果逐渐减少。 因此,我们预测当路径长度超过 6 时结果会下降。

- 实验结果表明,TPath 在 Hits@1、Hits@3 和 MRR 上优于 ICEWS 和 GDELT 的当前方法,但我们的结果略低于 NeuralLP 在 Hits@10 上的两个数据集和 DistMult 在 Hits@10 上超过 GDELT 的结果,如表 4 所示。 然后,表 5 显示了一些特定的时间推理路径,这意味着我们的模型可以得到特定的时间推理路径,而不是隐式推理向量。 接下来,我们将我们的模型与 MINERVA 方法在 KG 中进行多跳推理进行比较,我们的模型在数据集中的前 3 个关系中明显优于它。 此外,图 6 表明,out 模型可以在不同的固定长度下训练多跳推理,并在长度为 3 时获得最佳性能。
结论
- 在本文中,我们提出了 TPath,它考虑了时间信息并在时间知识图中选择特定的多跳推理路径。 更重要的是,我们提出了一个策略网络,可以训练代理学习时间多跳推理路径。 考虑到时间推理路径的多样性,我们提出了奖励函数。 此外,我们分析了时间推理路径,并在多跳推理任务上取得了最先进的结果。 然而,推理路径的固定长度可能是一个限制,需要进一步改进。
- 对于未来的工作,我们期望研究同时训练各种长度的时间推理路径的可能性。 模型可以根据设计奖励选择不同长度的推理路径,而不是每个实验中的固定长度。 此外,多跳路径推理在时间知识图谱中有广泛的应用,包括推荐系统、智能检索等。我们还考虑利用 TKG 中的空间信息来进一步提高推理路径的性能。