《Overlapping Community Detection at Scale: A Nonnegative Matrix Factorization Approach》
BIGCLAM(Cluster Affiliation Model for Big Networks,大型网络的聚类关系模型)是一个bipartite affiliation network模型。
BigCLAM方法流程:
第一步:定义一个基于节点-社区隶属关系生成图的模型(community affiliation graph model (AGM))
第二步:给定图,假设其由AGM生成,找到最可能生成该图的AGM
通过这种方式,我们就能发现图中的社区。
community affiliation graph model (AGM)
《Community-affiliation graph model for overlapping network community detection》
通过节点-社区隶属关系(下图左图)生成相应的网络(下图右图)。
参数为节点 V,社区 C ,成员关系 M,每个社区 c 有个概率
p
C
p_C
pC?
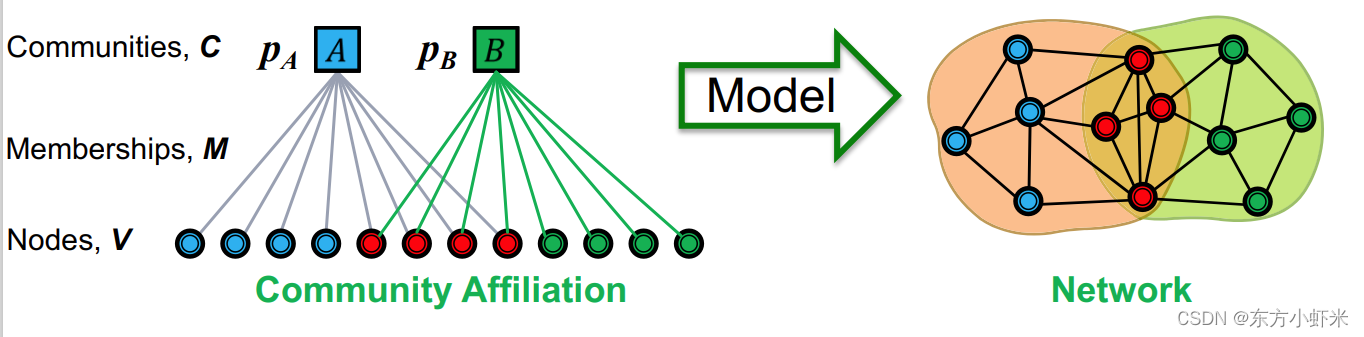
AGM生成图的流程
给定参数 ( V , C , M , { p C } ) (V,C,M,\lbrace p_C\rbrace) (V,C,M,{pC?}),每个社区 c 内的节点以概率 p C p_C pC?互相链接。
对同属于多个社区的节点对,其相连概率就是: p ( u , v ) = 1 ? ∏ c ∈ M u ? M v ( 1 ? p C ) p(u,v) = 1 - \prod_{c\in M_u \bigcap M_v}(1-p_C) p(u,v)=1?∏c∈Mu??Mv??(1?pC?)
(注意:如果节点 u 和 v没有共同社区,其相连概率就是0。为解决这一问题,我们会设置一个 background “epsilon” 社区,每个节点都属于该社区,这样每个节点都有概率相连 p ( u , v ) = ? p(u,v) = \epsilon p(u,v)=? 论文中建议 ? = 2 ∣ E ∣ ∣ V ∣ ( ∣ V ∣ ? 1 ) \epsilon = \frac{2|E|}{|V|(|V|-1)} ?=∣V∣(∣V∣?1)2∣E∣?)
AGM可以生成稠密重叠的社区
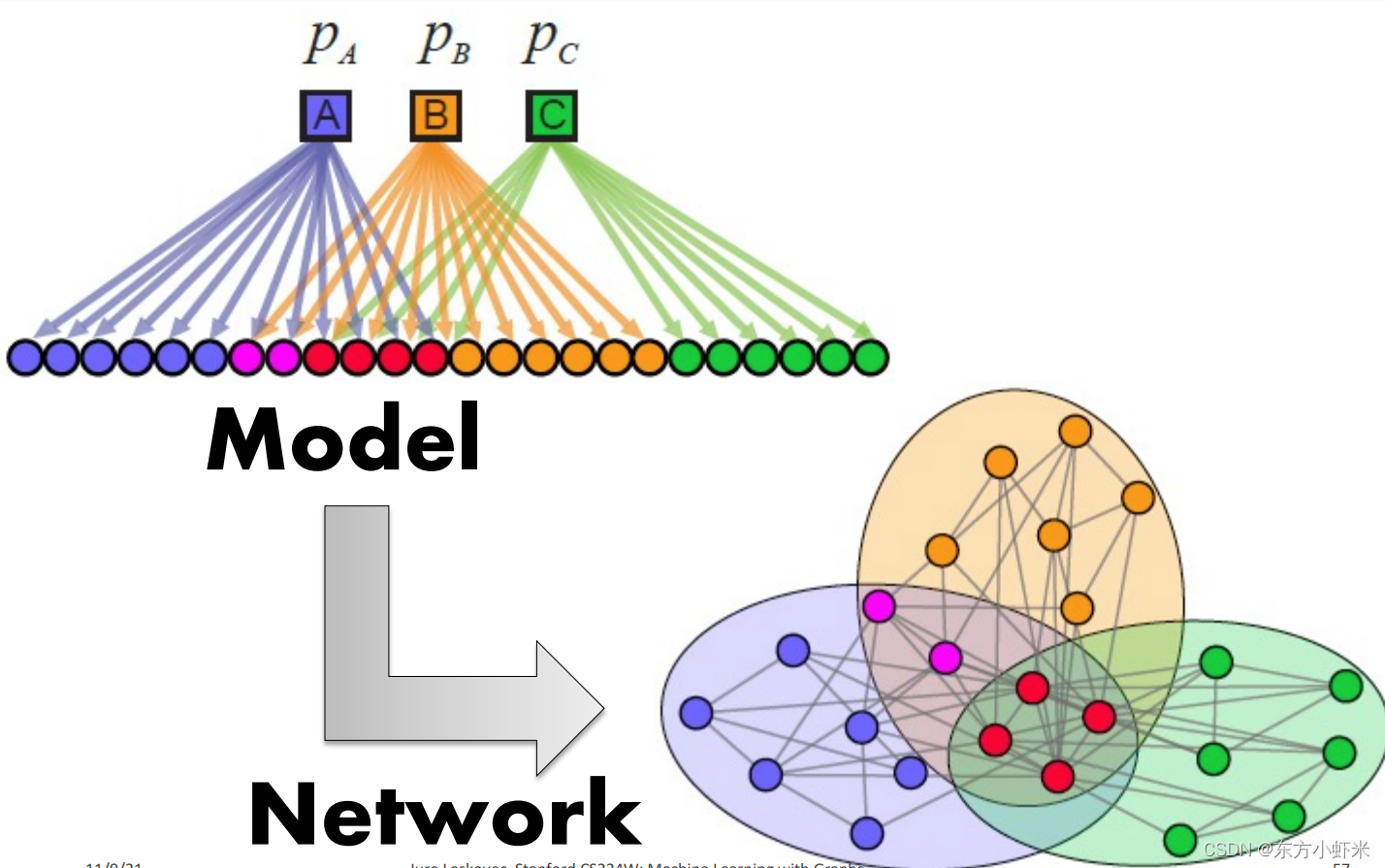
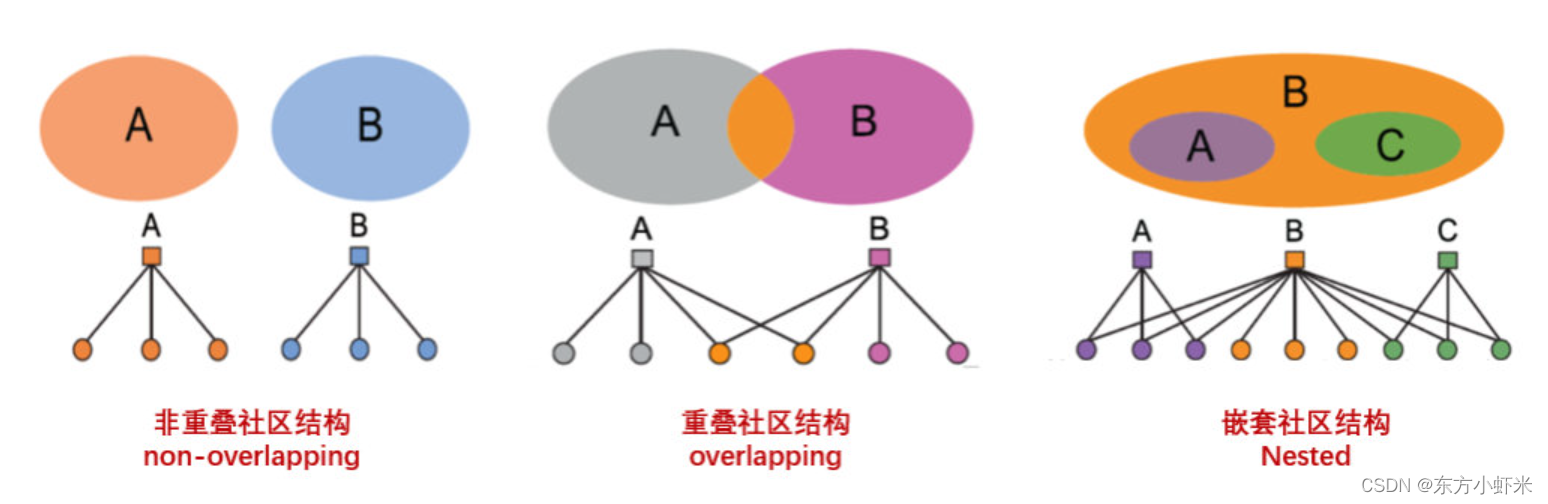
虽然,AMG模型是在重叠社区挖掘的时候引入的,但并不意味着AMG模型只能生成有重叠社区的网络。事实上,其非常灵活,可以生成不同类型的社区结构。如
通过AGM发现社区:给定图,找到最可能产生出该图的AGM模型参数(最大似然估计)
图拟合(graph fitting)
通过前面我们知道AGM的参数主要有三个:
- 节点归属关系 𝑀
- 社区内连接概率 p c p_c pc?
- 社区数 𝐶
给定一张图G
我们需要找到 F = a r g m a x P ( G ∣ F ) F = argmax P(G|F) F=argmaxP(G∣F)
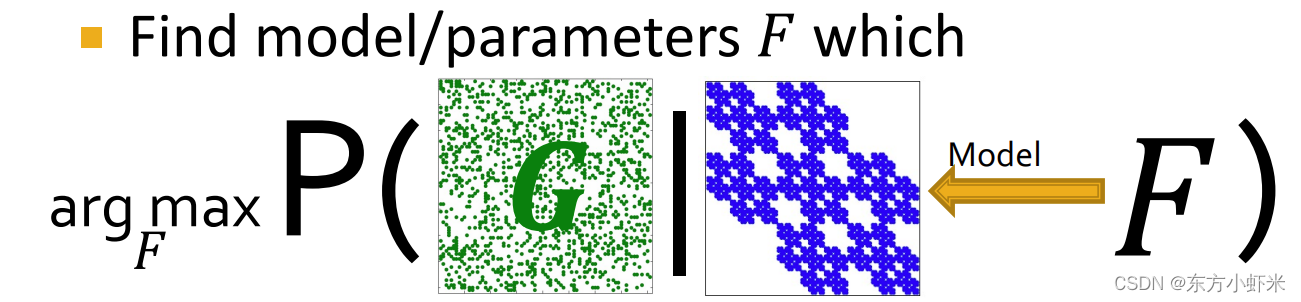
为了解决这一问题,我们需要高效的计算 P ( G ∣ F ) P(G|F) P(G∣F), 然后最大化F(使用梯度下降等优化算法)
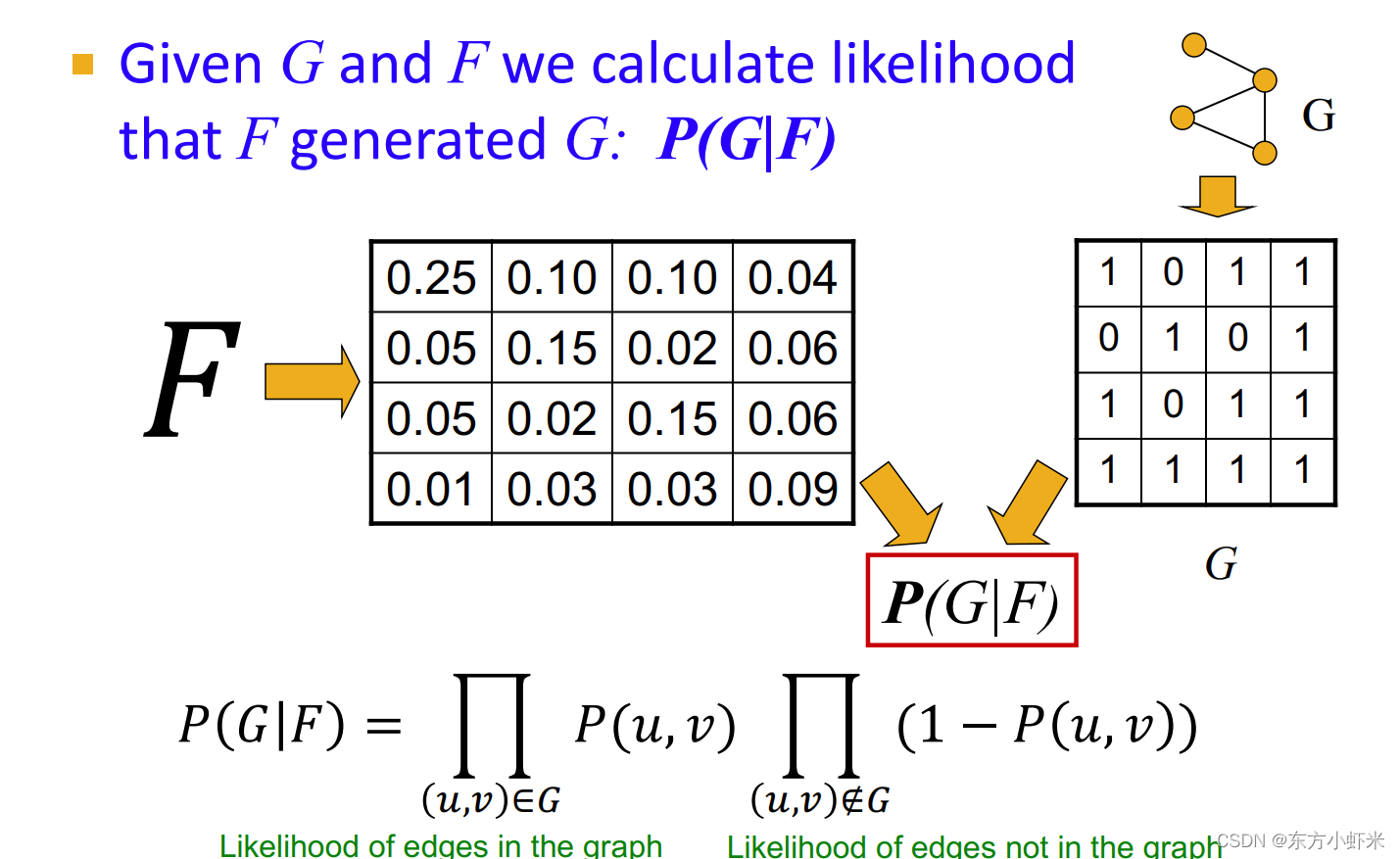
graph likelihood P ( G ∣ F ) P(G|F) P(G∣F)
通过F得到边产生的概率矩阵P(u,v), G具有邻接矩阵,从而得到 P ( G ∣ F ) = ∏ ( u , v ) ∈ G P ( u , v ) ∏ ( u , v ) ? G ( 1 ? P ( u , v ) ) P(G|F) = \prod_{(u,v)\in G}P(u,v) \prod_{(u,v)\notin G}(1-P(u,v)) P(G∣F)=∏(u,v)∈G?P(u,v)∏(u,v)∈/?G?(1?P(u,v))
即通过AGM产生原图的概率。(原图中有的边乘以生成概率,没有的边乘以不生成的概率(1-生成概率))
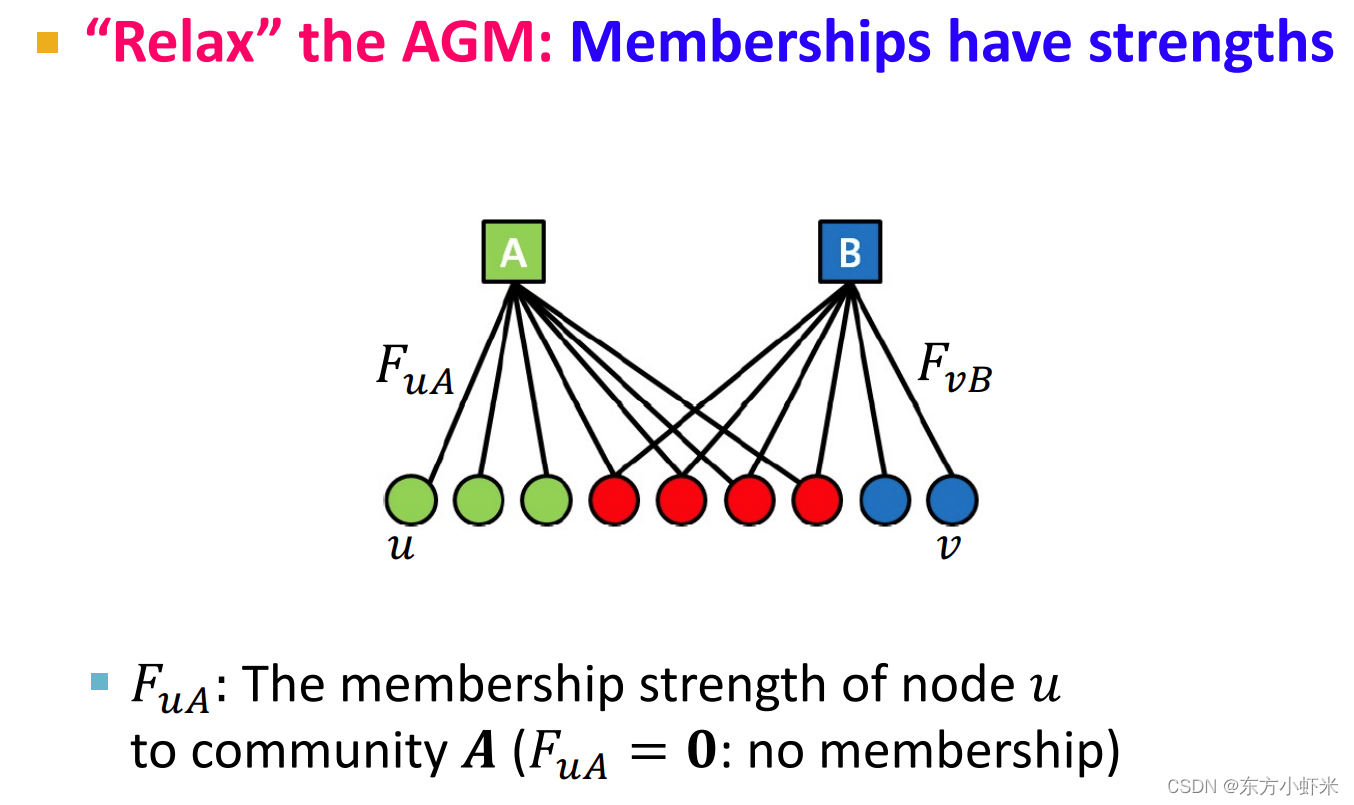
前面是普通的AGM。而BIGCLAM作为AGM的松弛版本,改进之处在于增加了边权重,采用了NMF方法等。
松弛AGM(“Relax” the AGM)
成员关系具有strength(如图所示): F u A F_uA Fu?A是节点 u属于社区 A 的成员关系的strength(如果 F u A = 0 F_uA = 0 Fu?A=0,说明没有成员关系(strength非负)
对于社区C,其内部节点u,v的链接概率为: P c ( u , v ) = 1 ? e x p ( ? F u C ? F v C ) P_c(u,v) = 1 - exp(-F_uC \cdot F_vC) Pc?(u,v)=1?exp(?Fu?C?Fv?C)
0 ≤ P c ( u , v ) ≤ 1 0\leq P_c(u,v)\leq1 0≤Pc?(u,v)≤1
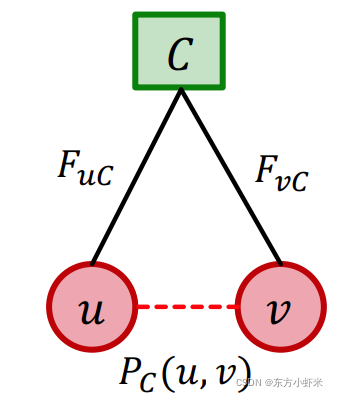
P c ( u , v ) = 0 P_c(u,v) = 0 Pc?(u,v)=0(节点之间无链接) 当且仅当 F u C ? F v C = 0 F_uC \cdot F_vC = 0 Fu?C?Fv?C=0(至少有一个节点对社区C没有成员关系)
P c ( u , v ) ≈ 1 P_c(u,v) \approx 1 Pc?(u,v)≈1(节点之间无链接) 当且仅当$F_uC \cdot F_vC $ 很大(两个节点都对社区C有强成员关系strength)
节点对之间可以通过多个社区相连,如果在至少一个社区中相连,节点对就相连,u,v至少在一个社区相连的概率为:

P ( u , v ) = 1 ? ∏ C ∈ T ( 1 ? P C ( u , v ) ) P(u,v) = 1 - \prod_{C\in T}(1-P_C(u,v)) P(u,v)=1?∏C∈T?(1?PC?(u,v)) 减数就是u与v在任何社区都不相连的概率

所以节点连接的概率与共享成员们的强度(两点同属于的社区数)成正比 P ( u , v ) = 1 ? e x p ( ? F u T F v ) P(u,v) = 1 - exp(-F_u^TF_v) P(u,v)=1?exp(?FuT?Fv?)
BigCLAM model
给定一个网络G(V,E), 我们最大化G在我们模型下的似然度
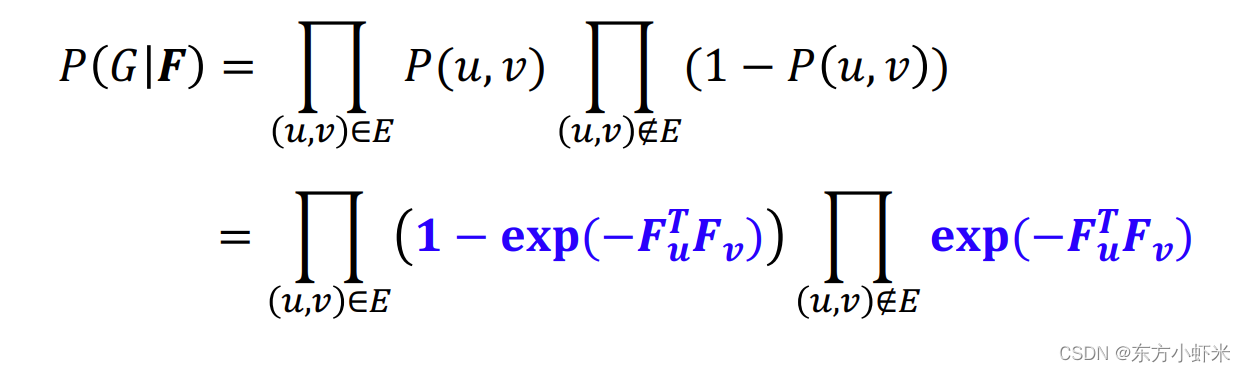
但是直接用概率的话,其值就是很多小概率相乘,数字小会导致numerically unstable的问题,所以要用log likelihood

优化$ l( F )$:从随机成员关系F开始,迭代直至收敛:
对每个节点u,固定其它节点的membership、更新 F u F_u Fu?。我们使用梯度提升的方法,每次对 F u F_u Fu?做微小修改,使log-likelihood提升。
对
F
u
F_u
Fu?的偏微分等于:
在梯度提升时候,前部分与u的度数线性相关(快),后部分与图中节点数线性相关(慢)
因此我们可以将后者分解: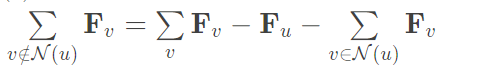
右式第一项可以提前计算并缓存好,每次直接用;后两项与u的度数线性相关。这样整个梯度步花费u的度数的线性时间。
总计来说,梯度步骤如下:

当我们找到了F,就可以生成想要的重叠社区,进而完成了我们的社区划分。
F还可以通过GNN获得
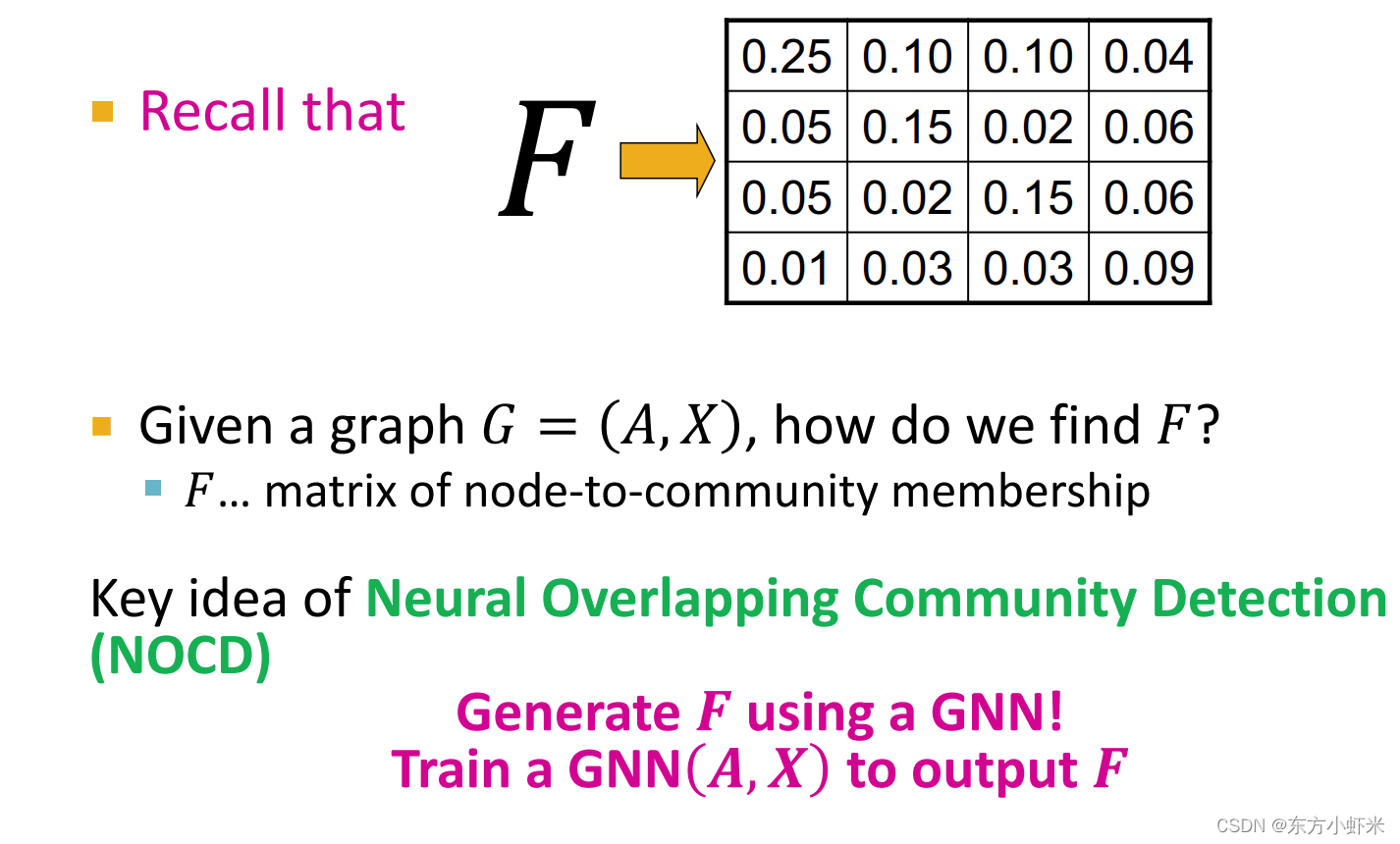
使用GNN的好处:
- GNN可以推广到其他图。否则,我们需要为每个新图优化𝐹
- GNN很好地利用了图结构——邻接矩阵𝑨和节点特征𝑿(例如:𝑋包括职业,爱好,教育在FB图上的用户。在对FB图进行训练后,GNN可能会从Instagram / Twitter推广到另一个社交网络。)

但是真实世界的图形通常是极其稀疏的, ∣ E ∣ n 2 < < 1 \frac{|E|}{n^2}<<1 n2∣E∣?<<1,即真是存在的边 比可能存在的边小很多。
式子第二部分的贡献要大得多。解决方法:取两项平均值
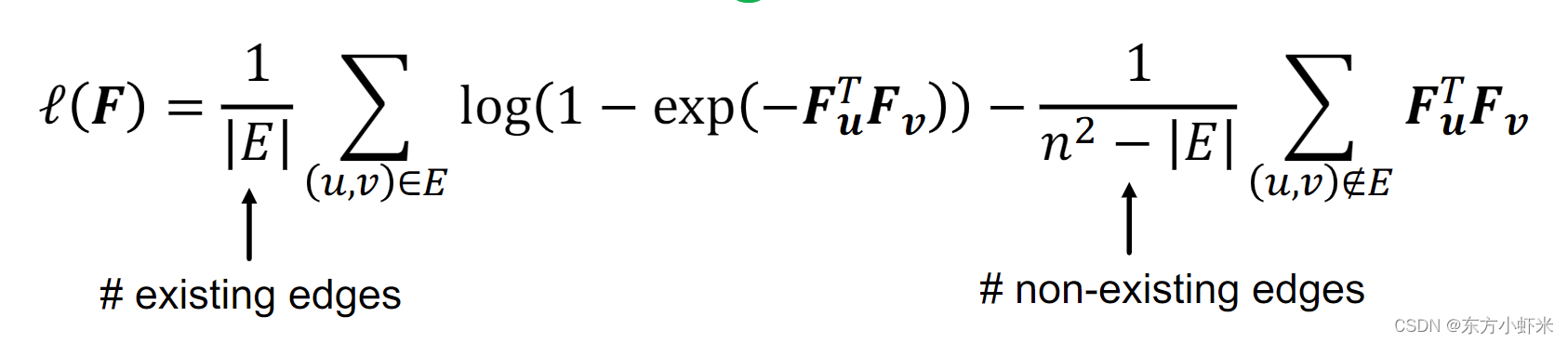
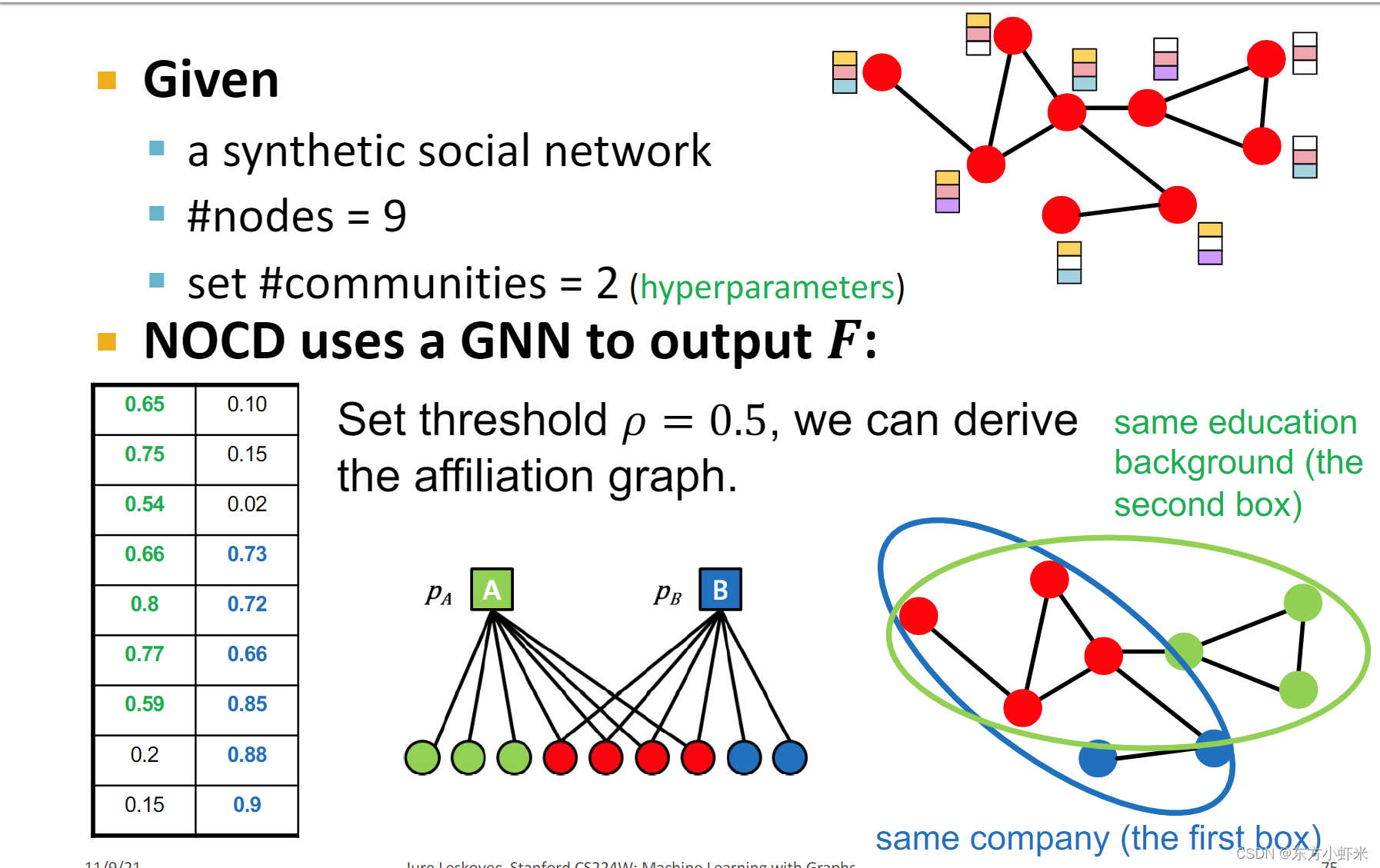
优化好F后,我们将节点分配给社区:
设置一个阈值𝜌:超参数,NOCD选择𝜌= 0.5
将节点𝑢分配到社区𝐶 如果 F u C > p F_uC>p Fu?C>p
一个实例:
BigCLAM总结:
BigCLAM定义了一个模型,可生成重叠社区结构的网络。给定图,BigCLAM的参数(每个节点的membership strength)可以通过最大化对数似然估计得到,这样我们就能得到社区划分的结果。
import numpy as np
import networkx as nx
def sigm(x):
# sigmoid操作 求梯度会用到
# numpy.divide数组对应位置元素做除法。
return np.divide(np.exp(-1. * x), 1. - np.exp(-1. * x))
def log_likelihood(F, A):
# 代入计算公式计算log似然度
A_soft = F.dot(F.T)
# 用邻接矩阵可以帮助我们只取到相邻的两个节点
FIRST_PART = A * np.log(1. - np.exp(-1. * A_soft))
sum_edges = np.sum(FIRST_PART)
# 1-A取的不相邻的节点
SECOND_PART = (1 - A) * A_soft
sum_nedges = np.sum(SECOND_PART)
log_likeli = sum_edges - sum_nedges
return log_likeli
def gradient(F, A, i):
# 代入公式计算梯度值
N, C = F.shape
# 通过邻接矩阵找到相邻 和 不相邻节点
neighbours = np.where(A[i])
nneighbours = np.where(1 - A[i])
# 公式第一部分
sum_neigh = np.zeros((C,))
for nb in neighbours[0]:
dotproduct = F[nb].dot(F[i])
sum_neigh += F[nb] * sigm(dotproduct)
# 公式第二部分
sum_nneigh = np.zeros((C,))
# Speed up this computation using eq.4
for nnb in nneighbours[0]:
sum_nneigh += F[nnb]
grad = sum_neigh - sum_nneigh
return grad
def train(A, C, iterations=100):
# 初始化F
N = A.shape[0]
F = np.random.rand(N, C)
# 梯度下降最优化F
for n in range(iterations):
for person in range(N):
grad = gradient(F, A, person)
F[person] += 0.005 * grad
F[person] = np.maximum(0.001, F[person]) # F应该大于0
ll = log_likelihood(F, A)
print('At step %5i/%5i ll is %5.3f' % (n, iterations, ll))
return F
# 加载图数据集
def load_graph(path):
G = nx.Graph()
with open(path, 'r') as text:
for line in text:
vertices = line.strip().split(' ')
source = int(vertices[0])
target = int(vertices[1])
G.add_edge(source, target)
return G
if __name__ == "__main__":
# adj = np.load('data/adj.npy')
G = load_graph('data/club.txt')
# adj = np.array(nx.adjacency_matrix(G).todense())
adj = nx.to_numpy_array(G) # 邻接矩阵
F = train(adj, 4)
F_argmax = np.argmax(F, 1)
for i, row in enumerate(F):
print(row)
输出成员强度f,需要现给定社区个数, f代表了属于买个社区的概率。设置阈值就可以实现社区划分。
[0.001 0.13812703 0.95775962 0.001 ]
[0.001 0.65957653 0.001 0.001 ]
[0.001 0.88928046 0.001 0.001 ]
[0.001 0.90021047 0.001 0.001 ]
[0.001 0.001 0.70842418 0.001 ]
[0.001 0.001 0.32002381 0.55196496]