一、手写高斯牛顿法
步骤:
1、先根据模型生成x,y的真值,并在真值中添加高斯分布的噪声
2、使用高斯牛顿法进行迭代
3、求解高斯牛顿法的增量方程?
增量方程的推到过程

?图片来源?? ?该公式等同于133页6.41式
Σ 是 高斯噪声的方差
CMakeLists.txt
cmake_minimum_required(VERSION 3.0)
project(ch6)
set(CMAKE_BUILD_TYPE Release)
set(CMAKE_CXX_FLAGS "-std=c++11")
#opencv
find_package(OpenCV REQUIRED)
#eigen
include_directories(${Opencv_INCLUDE_DIRS}
"/usr/inlcude/eigen3")
add_executable(gaussNewton gaussNewton.cpp)
target_link_libraries(gaussNewton ${OpenCV_LIBS})
代码:
? ? ? ? ?理一下思路
? ? ? ? ?要先算出J 矩阵, 利用J 矩阵 算出H矩阵? ? ??
? ? ? ? ?之后解线性方程组 Hx=b
? ? ? ? ?判断最后的cost满足调节没有,满足就不用迭代? ?(cost = error * error)
? ? ? ? 步骤
? ???????①定义误差函数error? ? yi=y_data[i] ? ?error=yi-exp(ae*x*x+be*x+ce)//用真实值减去估计值得到误差函数
? ? ? ? ?②J矩阵是误差函数对各个进行优化的系数的导数所组成的列向量
J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce); // d(error) /d(ae)
J[1] = -xi * exp(ae * xi * xi + be * xi + ce); // d(error) /d(be)
J[2] = -exp(ae * xi * xi + be * xi + ce); // d(error) /d(ce)? ? ? ? ?③然后是关于 H 矩阵在程序中的表达形式(看下图,这里出现的 w_sigma 和inv_sigma 是程序开始定义好的)
? ? ? ? ?
? ? ? ? ? g(x)? 也是同理? g = - inv_sigma? * inv_sigma * error * J? (error是误差函数,也就是高斯牛顿法中的 f(x)? )。
? ? ? ? ④求解 H x = g
? ? ? ? 用cholesky分解 (ch3课后题有6种方法求解线性方程组)
? ? ? ? ⑤判断cost的值是否大于lastcost,
????????如果本次迭代误差大于上次迭代误差,迭代结束。
(1)w_sigma 和 inv_sigma
设定噪声服从的正态分布的sigma值 double w_sigma = 1.0;
计算sigma的倒数,之后用于计算信息矩阵?double inv_sigma = 1.0 / w_sigma;
(2)rng.gaussian(val)表示生成一个服从均值为0,标准差为val的高斯分布的随机数
rng.gaussian(w_sigma * w_sigma)为随机数产生高斯噪声
w_sigma*w_sigma是噪声方差
//y=真实函数生成再加上高斯噪声
double ?y = exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma);
//这里把每个自变量所对应的真实值(y)算了出来,用作观测值(3)isnan()函数
判断是否是非法数字,?是非法数字返回真,nan全称为not a number
非法数字包含:负数开方,负数求对数,及0/0,0*inf,inf/inf,inf-inf等未定式
如果方程无解,那么dx[0]是非法字符nan,退出迭代
(4)chrono库
这里可以用c++11的新特性auto定义变量,写代码的时候不用那么麻烦
#include<chrono>
auto t1 = chrono::steady_clock::now();
auto t2 = chrono::steady_clock::now();
auto time_used = t2-t1;
cout<<"迭代所消耗时间 :"<<chrono::duration<double> (time_used).count()<<"秒"<<endl;c++的优化库:Ceres库 和 基于图优化的g2o库。
二、使用Ceres拟合曲线
Ceres是一个广泛使用的最小二乘问题求解库。
Ceres的求解过程包括代价函数的构建、最小二乘问题的构建以及最小二乘问题的求解。
1.代价函数的构建(cost function):详细内容看书,代价函数 y-exp(a*x*x+b*x+c)
2.最小二乘问题的构建:
最小二乘问题的构建主要采用Ceres::Problem类进行:
Problem::AddResidualBlock( )
AddResidualBlock()顾名思义主要用于向Problem类传递残差模块的信息,函数原型如下,传递的参数主要包括代价函数模块、损失函数模块和参数模块。
ResidualBlockId Problem::AddResidualBlock(CostFunction *cost_function,?
?? ??? ??? ??? ??? ??? ??? ??? ??? ??? ? ?LossFunction *loss_function,?
?? ??? ??? ??? ??? ??? ??? ??? ??? ??? ? ?const vector<double *> parameter_blocks)
cost_function:代价函数loss_function:损失函数,若构建的问题为无约束的最小二乘问题,则传入参数为nullptrparameter_blocks:参数块,也即最终求解的参数
?代价函数CostFunction的求导模型:
较为常用的包括以下三种:
?????1.自动导数(AutoDiffCostFunction):由ceres自行决定导数的计算方式,最常用的求导方式。
? ? ?2.数值导数(NumericDiffCostFunction):由用户手动编写导数的数值求解形式,通常在残差函数的计算使用无法直接调用的库函数,导致调用AutoDiffCostFunction类构建时使用;但手动编写的精度和计算效率不如模板类,因此不到不得已,官方并不建议使用该方法。
? ? ?3.解析导数(Analytic Derivatives):当导数存在闭合解析形式时使用,用于可基CostFunciton基类自行编写;但由于需要自行管理残差和雅克比矩阵,除非闭合解具有具有明显的精度和效率优势,否则同样不建议使用。
可以看出,ceres官方极力推荐用户使用自动求导方式AutoDiffCostFunction,这里也主要以AutoDiffCostFunction为例说明。
AutoDiffCostFunction为模板类,构造函数如下:
ceres::AutoDiffCostFunction<CostFunctor, int residualDim, int paramDim>(
CostFunctor* functor);模板参数依次为仿函数(functor)类型CostFunctor,残差维数residualDim和参数维数paramDim,接受参数类型为仿函数指针CostFunctor*。
CostFunctor:即为第一步构建的代价函数residualDim:残差块维度,也即模型的输出维度paramDim:参数块维度,也即模型的输入维度functor:指针,为代价函数的构造?
?对于本代码可以进行以下构建:
ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(new CURVE_FITTING_COST(x_data[i], y_data[i]))
//1 是问题中的误差ei 3 是曲线的参数最后对于该问题,构建残差项的配置如下:
// 残差项配置
ceres::Problem problem;
problem.AddResidualBlock(
new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(new CURVE_FITTING_COST(x_data[i], y_data[i])),
nullptr,
abc);
此处,未用到损失函数(无约束)故而传入nullptr;参数块为三维矩阵abc
注意:
由于在优化过程中,我们不希望因为程序的误操作导致操作符()重载的内容被修改,因此需要为函数体加上const关键字修饰。同理,在残差的计算过程中,为了避免除ceres优化之外的误操作引起待优化变量的改变,需要同时使用const关键字修饰参数类型和参数名保证类型和内容均不变;而residual只需要保证类型不变,参数每次都是可变的,因此只需要使用const修饰类型T即可。
3.最小二乘的求解
使用ceres::Solve进行求解,其函数原型如下:
void Solve(const Solver::Options& options, Problem* problem, Solver::Summary* summary)
options:求解器的配置,求解的配置选项problem:求解的问题,也即我们构建的最小二乘问题summary:求解的优化信息,用于存储求解过程中的优化信息
对求解器的配置介绍:
minimizer_type:迭代的求解方式,可选如下:
TRUST_REGION:信赖域方式,默认值LINEAR_SEARCH:线性搜索方法- 参数通常保持默认值即可
trust_region_strategy_type:信赖域策略,可选如下:
LEVENBERG_MARQUARDT,列文伯格-马夸尔特方法,默认值DOGLEG:Dog-leg法,俗称狗腿法linear_solver_type:求解线性方程组的方式
DENSE_QR:QR分解法,默认值,用于小规模最小二乘求解DENSE_NORMAL_CHOLESKY和?SPARSE_NORMAL_CHOLESKY:CHolesky分解,用于有稀疏性的大规模非线性最小二乘求解CGNR:共轭梯度法求解稀疏方程DENSE_SCHUR和?SPARSE_SCHUR:SCHUR分解,用于BA问题求解ITERATIVE_SCHUR:共轭梯度SCHUR,用于求解BA问题num_threads:求解使用的线程数minimizer_progress_to_stdout:是否将优化信息输出至终端
- bool类型,默认为false。若设置为true输出根据迭代方法而输出不同:
- ①信赖域方法
- cost:当前目标函数的数值
- cost_change:当前参数变化量引起的目标函数变化
- |gradient|:当前梯度的模长
- |step|:参数变化量
- tr_ratio:目标函数实际变化量和信赖域中目标函数变化量的比值
- tr_radius:信赖域半径
- ls_iter:线性求解器的迭代次数
- iter_time:当前迭代耗时
- total_time:优化总耗时
- ②线性搜索方法
- f:当前目标函数的数值
- d:当前参数变化量引起的目标函数变化
- g:当前梯度的模长
- h:参数变化量
- s:线性搜索最优步长
- it:当前迭代耗时
- tt:优化总耗时
?
// Options
ceres::Solver::Options options;
// cholesky分解
options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;
// 输出优化信息
options.minimizer_progress_to_stdout = true;
?Solver::Summary
Solver::Summary为求解器以及各个变量的信息,常用成员函数如下:
BriefReport():输出单行的简单总结;FullReport():输出多行的完整总结。
//优化信息
ceres::Solver::Summary summary;
//开始优化
ceres::Solve(options, &problem,&summary);
//输出结果
cout<<summary.BriefReport()<<endl;
cout<<"最优结果: a,b,c = "<<endl;
for(auto i : abc){
cout<<i <<endl;
}参考:
Ceres详解(二) CostFunction_yuntian_li的博客-CSDN博客_ceres costfunction
Ceres 库:基础使用,以手写高斯-牛顿法为例_JasonLi的博客-CSDN博客
这里复习下模板内容
模板
c++除了面向对象思想外还有一种编程思想叫 泛型编程,主要利用的技术就是模板。c++提供了两种模板机制:函数模板和类模板。
1.函数模板:
//语法
template<typename T>
写一个函数template: 声明创建模板
typename : 表示其后面的符号是一种数据类型,可以用class代替
T :通用的数据类型
例子:交换两个数
template<typename T>
void my_swap(T &a , T &b){
T temp = a;
a = b;
b = temp;
}模板的局限性:如果是自定义数据类型,比如 T 是Person类,需要用具体话方式做特殊实现
例子:判断两个Person类对象p1和p2是否相对
//两数是否相等
class Person{
public:
Person(string name,int age){
this->m_name = name;
this->m_age = age;
}
string m_name;
int m_age;
};
template<typename T>
void my_Compare(T &a , T &b){
if(a==b)
{
cout<<"两数相等"<<endl;
}
else{
cout<<"两数不相等"<<endl;
}
}
void test01(){
Person p1("Tom",10);
Person p2("Jerry",10);
my_Compare(p1,p2); //程序报错
int a = 10;
int b = 10;
my_Compare(a,b);
}报错内容:无法比较两个Person类型
![]()
?解决方法:① 重载 ==?
? ? ? ? ? ? ? ? ? ②利用具体化Person实现代码
template<> void my_Compare(Person &a , Person &b){
if(a.m_name == b.m_name && a.m_age == b.m_age){
cout<<"相等"<<endl;
}else{
cout<<"不相等"<<endl;
}
}2.类模板:
//类模板
template<class NameType , class AgeType>
class Student
{
public:
Student(NameType name , AgeType age){
this->m_name = name;
this->m_age = age;
}
NameType m_name;
AgeType m_age;
};
void test02(){
Student<string, int> p1("qqq",18);
Student<string, int> p2("www",17);
cout<<p1.m_name<<" "<<p1.m_age<<endl;
}类模板:使用时必须指定类型?
三、使用g2o进行曲线拟合
g2o是一个基于图优化的库,是一种将非线性优化与图论结合起来的理论。
特点:
1.顶点为优化变量,边为误差项。
2.待估计的参数构成顶点,观测数据构成了边。
3.误差定义在边内,边附着在顶点上。
4.误差关于顶点的偏导数定义在边里的雅克比矩阵J上,而顶点的更新通过内置的oplusImpl函数实现更新。
5.在视觉slam中,相机的位姿与观测的路标构成图优化的顶点;相机的运动、路标的观测构成图优化的边。
学习g2o优化前建议先去看看g2o类图,这个非常重要。
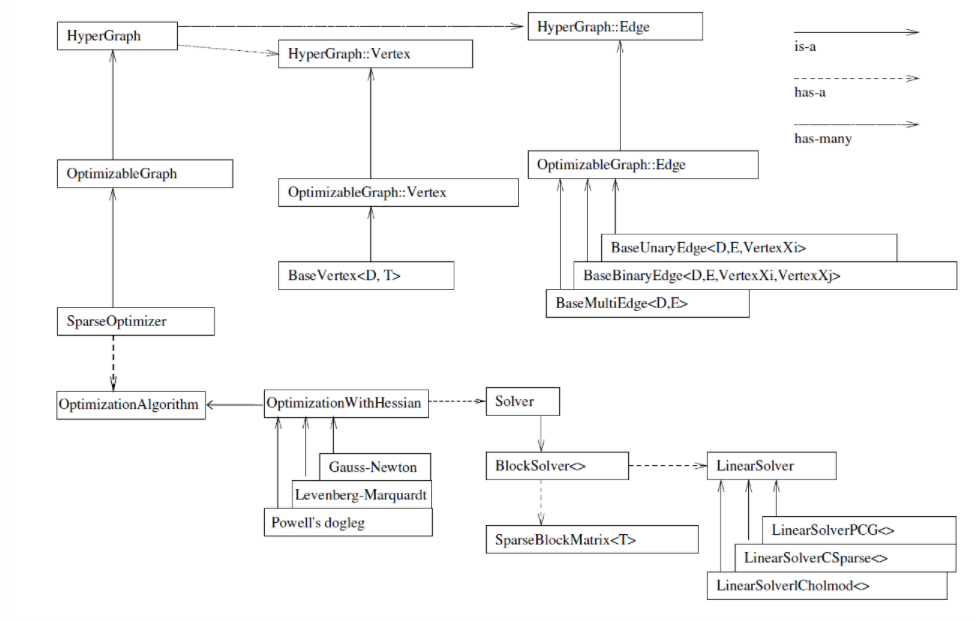
?详细讲解参考高博文章
在g2o中选择优化方法需三个步骤:
1.选择一个线性方程求解器(LinearSolver):PCG, CSparse, Choldmod;
2.选择一个BlockSolver, 包含SparseBlockMatrix,用于计算稀疏雅可比和海塞;BlockSolver用于计算迭代过程中最关键的一步HΔx=?b为一个线性方程的求解器。
3.选择一个迭代策略:GN, LM, Doglog。(一般选取前两种方法之一)
代码步骤:
- 定义顶点的类型
- 定义边的类型
- 构建图优化
配置块求解器BlockSolver,
配置线性方程求解器LinearSolver,从
PCG, CSparse, Choldmod、Dense中选一个作为求解方法配置总求解器solver,并从GN,LM,Dogleg优化算法中选一个,再用上述块求解器BlockSolver初始化
配置稀疏优化器SparseOptimizer
往图中增加顶点和边,并添加到SparseOptimizer
启动优化
流程:
1. 定义顶点的类型
?顶点主要的成员函数(位于 g2o/core/base_vertex.h 中):?
// 返回优化之后顶点的值.
const EstimateType& estimate() const { return _estimate;}自定义顶点时,需要重写4个函数:
virtual void setToOriginImpl(); // 顶点重置函数
virtual void oplusImpl(const double* update); // 顶点更新函数
virtual bool read(istream &in); // 读操作
virtual bool write(ostream &out) const; // 写操作setToOriginImpl为顶点的重置函数,用来设定待优化变量的初始值;oplusImpl为顶点更新函数,主要用于在使用增量方程计算出增量 Δ x 后,用来更新x (k+1) = x(k) +??Δ x;? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ?
read,write 函数可以不进行覆写,仅仅声明一下就可。
2.定义边的类型
?边的重要的成员变量和函数:
_measurement:存储观测值
_error:存储computeError() 函数计算的误差
_vertices[]:存储顶点信息,比如二元边的话,_vertices[] 的大小为2,存储顺序和调用setVertex(int, vertex) 是设定的int 有关(0 或1)
setId(int):来定义边的编号(决定了在H矩阵中的位置)
setMeasurement(type) 函数来定义观测值
setVertex(int, vertex) 来定义顶点
setInformation() 来定义协方差矩阵的逆自定义边时,需要重写4个函数:
?virtual void computeError(); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? // 误差计算函数
?virtual void linearizeOplus(); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? // 计算雅克比矩阵?
virtual bool read(istream &in); ? ? ? ? ? ? ? ? ? ? ? ? ? // 读操作
?virtual bool write(ostream &out) const; ? ? ? ? ? ? ? ? ? ? // 写操作
computeError 函数是使用当前顶点的值计算的测量值与真实的测量值之间的误差,为边的误差计算函数。
linearizeOplus 函数是在当前顶点的值下,该误差对优化变量的偏导数,即jacobian矩阵。这个函数计算了每条边相对于顶点的雅克比
3.构建图优化
3.1?配置块求解器? BlockSolver?
// 矩阵块求解器
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
//每个误差项优化变量维度为3,误差值维度为13.2 配置线性方程求解器 LinearSolver
// 线性求解器
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
?PCG, CSparse, Choldmod、Dense四种线性方程求解器
- LinearSolverPCG :使用preconditioned conjugate gradient 法,继承自 LinearSolver
- LinearSolverCSparse:使用 CSparse 法,继承自LinearSolverCCS;
- LinearSolverCholmod:使用 sparse?cholesky 分解法,继承自LinearSolverCCS;
- LinearSolverDense :使用 dense?cholesky 分解法,继承自 LinearSolver
3.3 配置总求解器solver,并从GN,LM,Dogleg优化算法中选一个,再用上述块求解器BlockSolver初始化
// 梯度下降方法,可以从GN, LM, DogLeg 中选
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
3.4?配置稀疏优化器SparseOptimizer
g2o::SparseOptimizer optimizer; // 稀疏优化器,图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
另一种写法:
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block; /// 顶点每个误差项优化变量维度为3,误差值维度为1(abc)
// 创建一个线性求解器 LinearSolver,采用 dense cholesky 分解法
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器
// 稀疏矩阵块求解器 用于求解 雅克比J ( 得到右边 b = e转置 * Ω * J ) 和 海塞矩阵 H 左边 H = J转置* Ω * J
//构造线性方程的矩阵块,并用上面定义的线性求解器初始化
Block* solver_ptr = new Block( linearSolver ); // 矩阵块求解器
// 迭代算法:梯度下降方法,GN, LM, DogLeg 中选;详看下面三行代码
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr ); //GN
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr ); //LM
g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr ); //DogLeg
g2o::SparseOptimizer optimizer; //稀疏 优化模型
optimizer.setAlgorithm( solver ); // 设置求解器
optimizer.setVerbose( true ); // 打开调试输出
3.5?往图中增加顶点和边,并添加到SparseOptimizer?
// 往图中增加顶点
CurveFittingVertex *vertex = new CurveFittingVertex();
vertex->setEstimate(待优化值); // 设置优化初始值
vertex->setId(0); // 设置顶点ID
optimizer.addVertex(vertex); // 向稀疏优化器添加顶点
// 往图中增加边
for (int i = 0; i < N; i++){
CurveFittingEdge *edge = new CurveFittingEdge(边);
edge->setId(i);
edge->setVertex(0, vertex); // 设置连接的顶点
edge->setMeasurement(观测数值); // 设置观测数值
edge->setInformation(信息矩阵); // 设置信息矩阵:协方差矩阵之逆
optimizer.addEdge(edge); // 向稀疏优化器添加边
}
4?启动优化????????
optimizer.initializeOptimization(); // 设置优化初始值
optimizer.optimize(10); // 设置优化次数
estimate = vertex->estimate(); // 执行优化参考:
曲线模型顶点和边代码遇到的问题:
1.?EIGEN_MAKE_ALIGNED_OPERATOR_NEW
Eigen库为了使用SSE加速,在内存上分配了128位的指针,涉及字节对齐问题。在生成定长的Matrix或Vector对象时,需要开辟内存,调用默认构造函数,通常x86下的指针是32位,内存位数没对齐就会导致程序运行出错。而对于动态变量(例如Eigen::VectorXd)会动态分配内存,因此会自动地进行内存对齐。
解决方法:在public下写一个宏EIGEN_MAKE_ALIGNED_OPERATOR_NEW
?
参考文章:Eigen字节对齐问题
? ? ? ? ? ? ? ? ??Eigen内存对齐
2. static_cast
static_cast 运算符 | Microsoft Docs
运算符可用于将指向基类的指针转换为指向派生类的指针
CMakeLists.txt
这里因为使用g2o库,执行? cmake? ..? 以后由于CMakeLists里书写错误会报错,参考文章
#视觉SLAM书上的程序使用的g2o版本比较旧了,使用的是c++11版本的g20。而自己在编译g2o的时候编译的是最新版本的g2o,里面大量使用了c++14标准库的一些新特性,比如std::index_sequence等等。而书上的CMakeLists.txt默认使用的是c++11进行cmake编译
set(CMAKE_CXX_STANDARD 14)
#g2o 使用它需要写依赖
list(APPEND CMAKE_MODULE_PATH /home/hope/Downloads/g2o/cmake_modules )
set(G2O_ROOT /usr/local/include/g2o)
find_package(G2O REQUIRED)
add_executable(g2oCurveFitting g2oCurveFitting.cpp)
target_link_libraries(g2oCurveFitting ${OpenCV_LIBS} ${G2O_CORE_LIBRARY} ${G2O_STUFF_LIBRARY})