这篇笔记是关于3篇文章的合集,它们分别是:
- 《Unsupervised Scale-consistent Depth and Ego-motion Learning from Monocular Video》
- 《Unsupervised Scale-consistent Depth Learning from Video》
- 《Auto-Rectify Network for Unsupervised IndoorDepth Estimation》
参考代码:
1. 概述
介绍:在自监督的深度估计算法中MonoDepth2一个较为经典的方法,文章的整体pipeline与其存在一定的相似性,都是输入连续视频帧作为输入,通过构建光度重构误差进行深度预测和相机位姿的修正。在这篇文中比较鲜明的创新点主要包含如下几点:
1)对于视频中存在物体运动、遮挡与一些困难像素区域(无纹理或是若纹理)情况提出了一种新的reweight机制,从而去降低这些像素在整体训练过程中的影响,从而提升深度自监督网络的训练稳定性;
2)自监督的深度估计方法在训练和测试中是使用不同的帧切片进行的,这就导致其深度预测的scale是不一致的,这就对后期恢复真实轨迹信息(视觉里程计)带来了困难,对此文章提出了一种对于帧间scale进行约束的方法。在此基础上再套用一个SLAM的上层架构便可以得到基于视频自监督的SLAM;
不过需要注意的是文章提出的scale一致性并不能代表深度预测的一致性和平滑性,这一点需要进行区分。
这篇博文的内容主要来自于上面提到的3篇文章,不过这里进行介绍的内容主要偏向于深度估计,所以像论文2中提到的涉及SLAM相关的内容这里不做更多扩展。
2. 方法设计
2.1 自监督深度估计pipeline
文章的深度估计pipeline见下图所示:
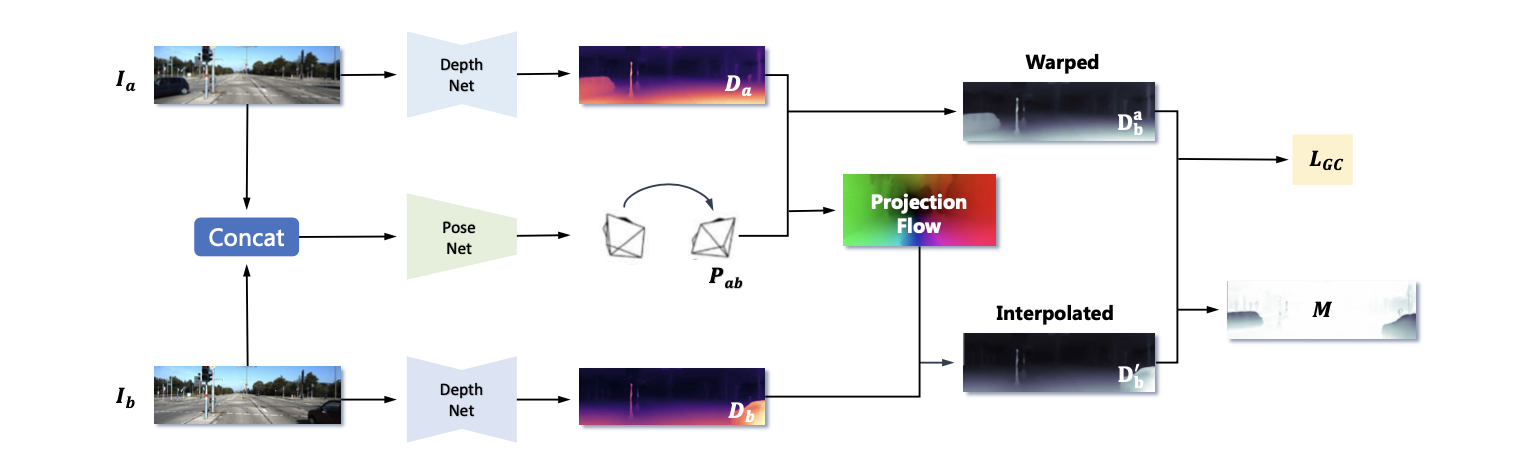
在上图中可以看到文章的方法与MonoDpeth2的方法很接近都是输入连续的2帧图像,通过DepthNet和PoseNet建立起图像之间的光度重构约束。输入的图像
(
I
a
,
I
b
)
(I_a,I_b)
(Ia?,Ib?)得到对应深度估计结果
(
D
a
,
D
b
)
(D_a,D_b)
(Da?,Db?)与相机位姿参数
P
a
b
P_{ab}
Pab?。则对于光度重构误差可以将其描述为如下形式:
L
p
=
1
∣
V
∣
∑
p
∈
V
λ
i
∣
∣
I
a
(
p
)
?
I
a
′
(
p
)
∣
∣
1
+
λ
s
1
?
S
S
I
M
a
a
′
(
p
)
2
L_p=\frac{1}{|V|}\sum_{p\in V}\lambda_i||I_a(p)-I_a^{'}(p)||_1+\lambda_s\frac{1-SSIM_{aa^{'}}(p)}{2}
Lp?=∣V∣1?p∈V∑?λi?∣∣Ia?(p)?Ia′?(p)∣∣1?+λs?21?SSIMaa′?(p)?
其中,
V
V
V是重投影之后有效像素的集合,
I
a
′
(
p
)
I_a^{'}(p)
Ia′?(p)是图像
I
a
I_a
Ia?重投影之后的图像。在此上按照输入图像作为引导对深度估计结果进行平滑约束:
L
s
=
∑
p
(
e
?
?
I
a
(
p
)
?
?
D
a
(
p
)
)
2
L_s=\sum_p(e^{-\nabla I_a(p)}\cdot\nabla D_a(p))^2
Ls?=p∑?(e??Ia?(p)??Da?(p))2
完成深度的自监督约束之后,接下来便是对物体运动、遮挡和困难像素区域的处理了,作者通过对实际这些像素所处的深度估计值进行分析之后,得出其深度预测值在相邻两帧上是存在较大差异的。则可以通过网络约束的形式将这些深度区域进行约束使其深度结果一致,从而提升深度估计质量。
PS: 虽然文章的算法里面对这样的假设通过贴图方式进行说明,但是这个假设过强,还需要在后序的严重细致分析才能断定。个人觉得还是过强,才有了后序的文章中也借用了MonoDepth中的auto-mask机制。
回过头再看一下文章对于深度差异的描述:
D
d
i
f
f
(
p
)
=
∣
D
b
a
(
p
)
?
D
b
′
(
p
)
∣
D
b
a
(
p
)
+
D
b
′
(
p
)
D_{diff}(p)=\frac{|D_b^a(p)-D_b^{'}(p)|}{D_b^a(p)+D_b^{'}(p)}
Ddiff?(p)=Dba?(p)+Db′?(p)∣Dba?(p)?Db′?(p)∣?
其中,
D
b
′
D_b^{'}
Db′?代表的是经过
D
b
D_b
Db?差值之后的结果。之所以这样做的原因是按照相机位姿warp之后的深度并不是在图像网格上对其的,因此使用差值的方式去减少误差,详见下图:
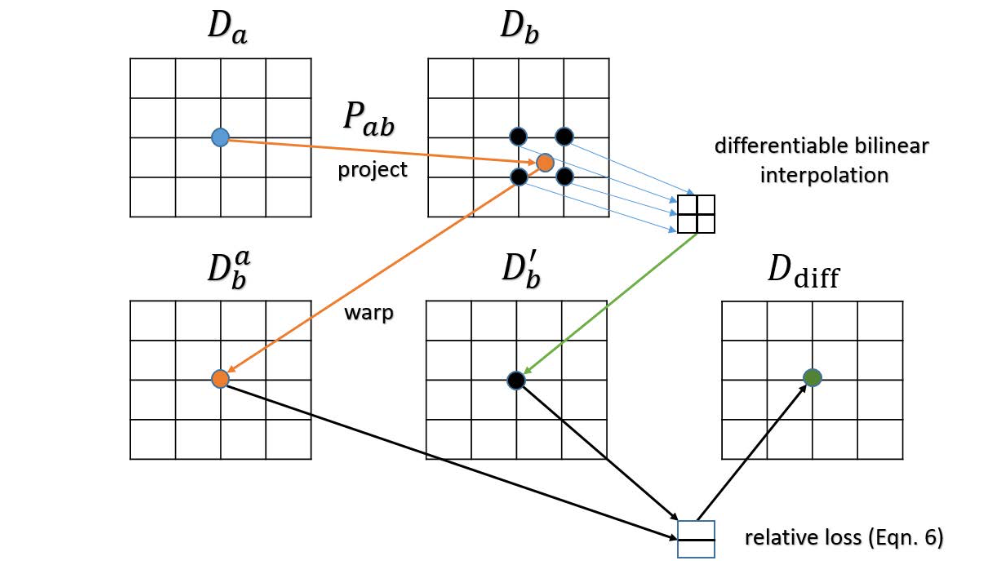
文章的意图是实现warp之后的深度差异最小化,则其约束描述为:
L
G
C
=
1
∣
V
∣
∑
p
∈
V
D
d
i
f
f
(
p
)
L_{GC}=\frac{1}{|V|}\sum_{p\in V}D_{diff}(p)
LGC?=∣V∣1?p∈V∑?Ddiff?(p)
更近一步将这里得到的信息运用到光度重构中的权重mask被描述为:
M
=
1
?
D
d
i
f
f
M=1-D_{diff}
M=1?Ddiff?
至于像上面提到的第二篇文章里面提到的ARN模块,其是建立在不同数据集的统计上来的,这里将KITTI和NYU数据集的旋转平移特性进行分析得到下面的像素分布:
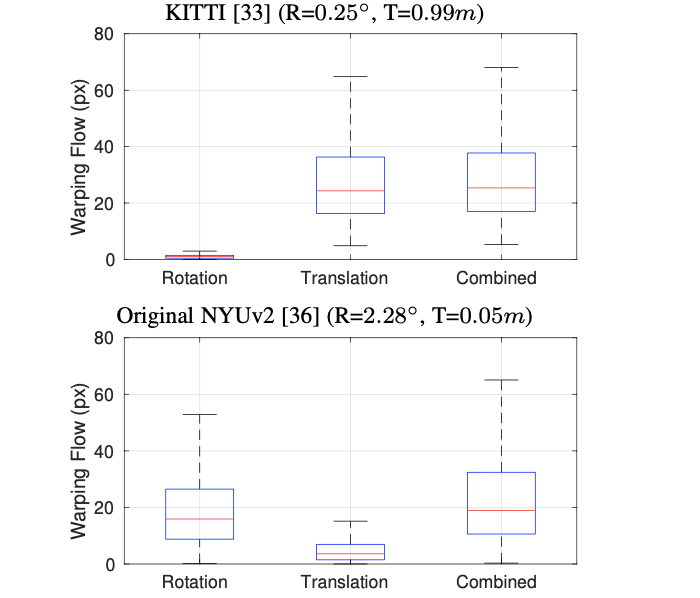
相当于说NYU数据集存在更多的旋转分量(因为手持),因而文章专门设计了一个ARN模块去减少旋转带来的影响,从而提升整体自监督深度估计的性能。这里更大程度上是提供了一种分析问题的思路,不同数据集情况也不一样,参考价值有限。
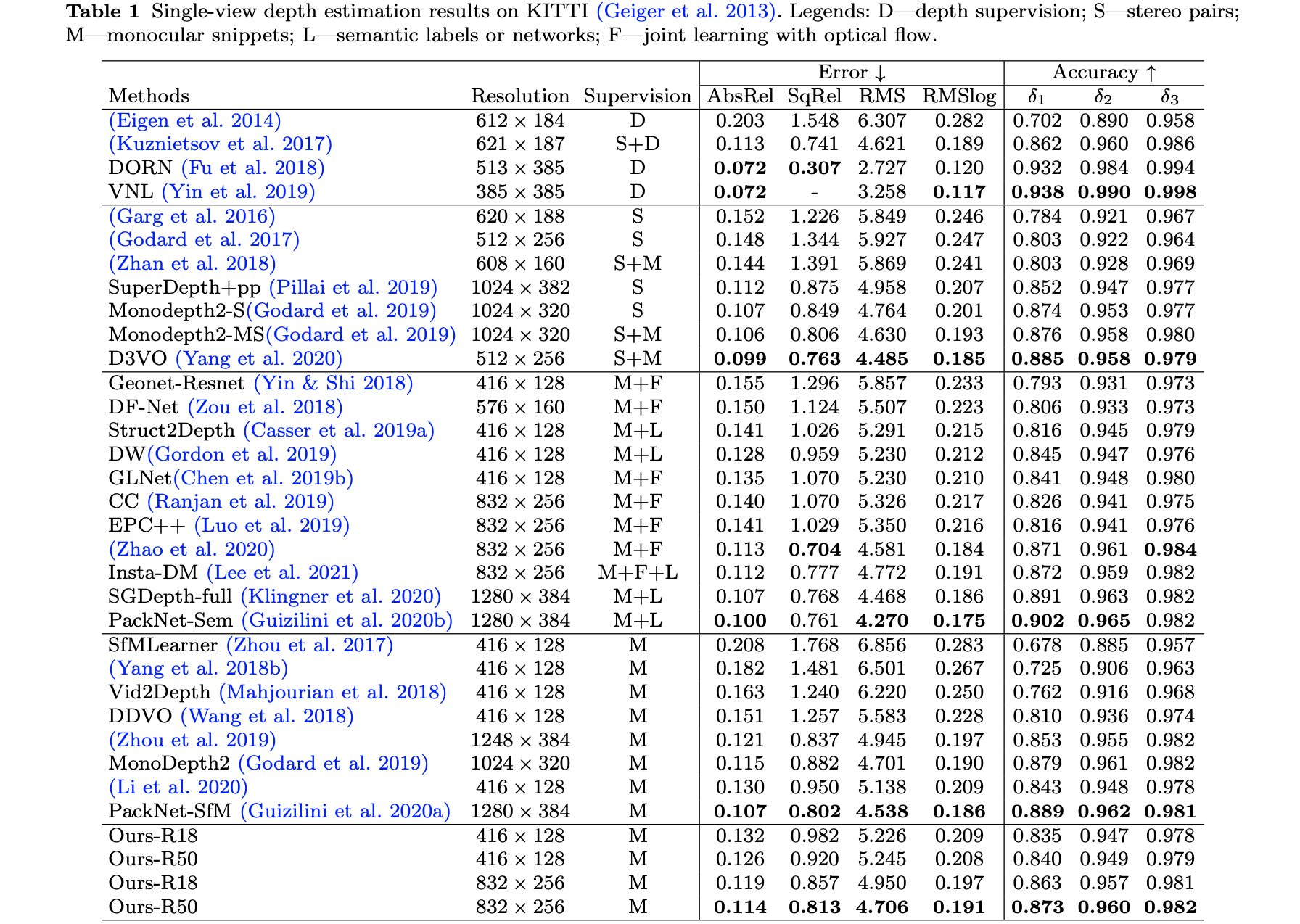
3. 实验结果
“SC-SfMLearner-Release”的性能比较:

“sc_depth_pl”的性能比较: