取样定理
1 信号的取样

定义
取样是利用取样脉冲序列
s
(
t
)
s(t)
s(t)从连续信号
f
(
t
)
f(t)
f(t)中“抽取”一系列离散样本值的过程;得到的离散信号称为取样信号。
f s ( t ) = f ( t ) s ( t ) f_s(t)=f(t)s(t) fs?(t)=f(t)s(t)
取样间隔 T s T_s Ts?,取样频率 f s = 1 / T s f_s=1/T_s fs?=1/Ts?
取样信号频谱:
F
s
(
j
ω
)
=
1
2
π
F
(
j
ω
)
?
S
(
j
ω
)
F_{s}(j \omega)=\frac{1}{2 \pi} F(j \omega) * S(j \omega)
Fs?(jω)=2π1?F(jω)?S(jω)
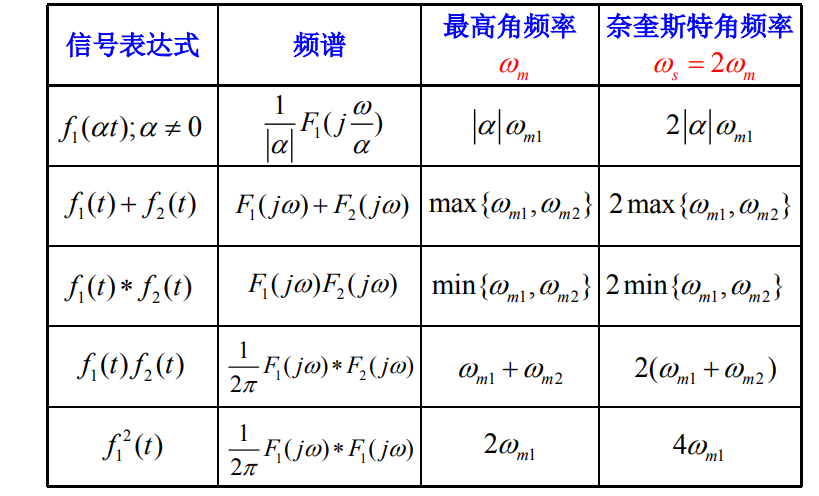
设 f ( t ) f(t) f(t)是带限信号, 即 f ( t ) f(t) f(t)的频谱只在区间 ( ? ω m , ω m ) (-\omega_m,\omega_m) (?ωm?,ωm?) 内为有限值,其余区间为0 。
f ( t ) ← → F ( j ω ) f(t) \leftarrow \rightarrow F(j \omega) f(t)←→F(jω)

矩形脉冲取样:
s
(
t
)
s(t)
s(t)是周期为
T
s
T_s
Ts?的矩形脉冲信号 (或称为开关函数)
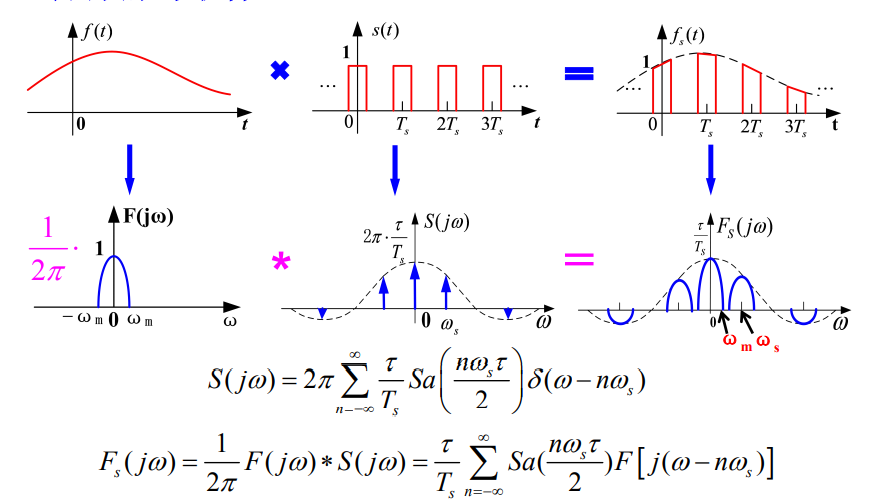
周期信号的频谱是脉冲序列。
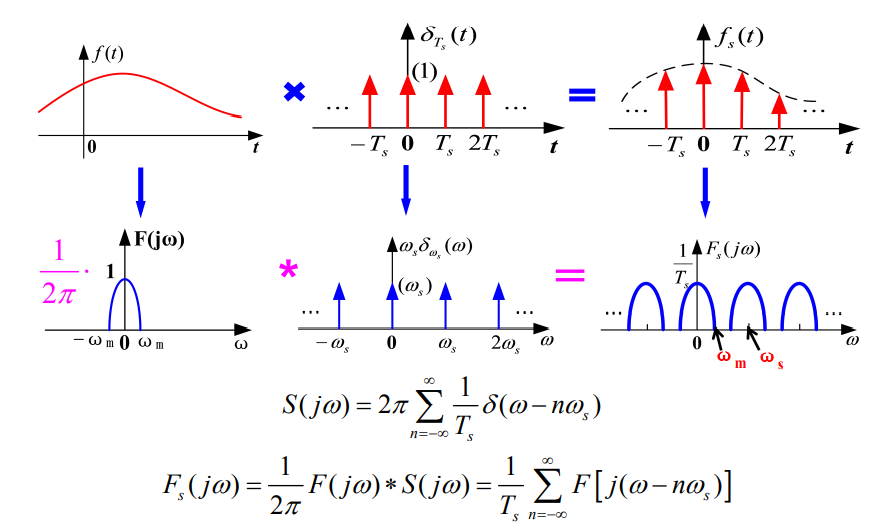
冲激取样:
s
(
t
)
s(t)
s(t)是周期为
T
s
T_s
Ts?的冲激函数序列
δ
T
s
(
t
)
\delta_{Ts}(t)
δTs?(t)
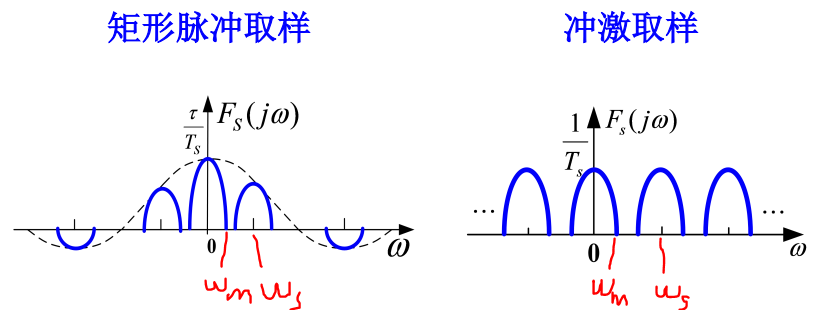
说明:画取样信号 f s ( t ) f_s(t) fs?(t)的频谱时,设定 ω s ≥ 2 ω m ω_s ≥2ω_m ωs?≥2ωm?,此时其频谱不发生混叠,因此可以利用低通滤波器从 F s ( j ω ) F_s(j\omega) Fs?(jω)中提取出 F ( j ω ) F(j\omega) F(jω),即从 f s ( t ) f_s(t) fs?(t)中恢复原信号 f ( t ) f(t) f(t)。否则将发生频谱混叠,而无法恢复原信号。
2 取样定理(时域)
重要意义:取样定理是连续信号与离散信号间的一座桥梁,为其相互转换提供了理论依据。在一定条件下,一个带限连续信号完全可以用其离散样本值表示。即这些样本值包含了该连续信号的全部信息,用它们可以恢复原信号。
由于 f s ( t ) = f ( t ) s ( t ) = f ( t ) ∑ n = ? ∞ ∞ δ ( t ? n T s ) = ∑ n = ? ∞ ∞ f ( n T s ) δ ( t ? n T s ) f_{s}(t)=f(t) s(t)=f(t) \sum_{n=-\infty}^{\infty} \delta\left(t-n T_{s}\right)=\sum_{n=-\infty}^{\infty} f\left(n T_{s}\right) \delta\left(t-n T_{s}\right) fs?(t)=f(t)s(t)=f(t)∑n=?∞∞?δ(t?nTs?)=∑n=?∞∞?f(nTs?)δ(t?nTs?)
当 w s ≥ w m w_s\ge w_m ws?≥wm?时,将冲激取样信号通过低通滤波器:
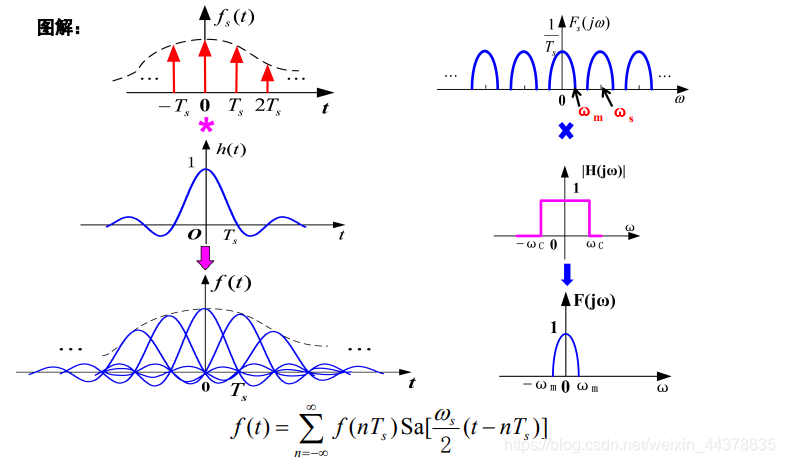
只要已知各取样值 f ( n T s ) f(nT_s) f(nTs?), 就可唯一地确定出原信号 f ( t ) f(t) f(t)。
时域取样定理:一个频谱在区间
(
?
w
m
,
w
m
)
(-w_m,w_m)
(?wm?,wm?)以外为0的带限信号
f
(
t
)
f(t)
f(t),可唯一地由其在均匀间隔
T
s
[
T
s
<
1
/
(
2
f
m
)
]
T_s[T_s<1/(2f_m)]
Ts?[Ts?<1/(2fm?)]上的样值点
f
(
n
T
s
)
f(nT_s)
f(nTs?)确定。
说明:为恢复原信号,必须满足两个条件:
(1) f ( t ) f(t) f(t)必须是带限信号;
(2)取样频率不能太低,必须
f
s
>
2
f
m
f_s>2f_m
fs?>2fm?,或者说,取样间隔不能太大,必须
T
s
<
1
/
(
2
f
m
)
T_s<1/(2f_m)
Ts?<1/(2fm?);否则将发生混叠。 通常把最低允许的取样频率
f
s
=
2
f
m
f_s=2f_m
fs?=2fm?称为奈奎斯特频率(Nyquist Sampling Rate),把最大允许的取样间隔
T
s
=
1
/
(
2
f
m
)
T_s=1/(2f_m)
Ts?=1/(2fm?) 称为奈奎斯特间隔(Nyquist Space)

3 取样定理(频域)
根据时域与频域的对偶性,可推出频域取样定理:
一个在时域区间 ( ? t m , t m ) (-t_m,t_m) (?tm?,tm?)以外为0的时限信号 f ( t ) f(t) f(t)的频谱函数 F ( j w ) F(jw) F(jw),可唯一地由其在均匀频率间隔 f s [ f s < 1 / ( 2 t m ) ] f_s[f_s<1/(2t_m)] fs?[fs?<1/(2tm?)]上的样值点 F ( j n w s ) F( jnw_s) F(jnws?)确定。
F ( j ω ) = ∑ n = ? ∞ ∞ F ( j n π t m ) S a ( ω t m ? n π ) , t m = 1 2 f s F(j \omega)=\sum_{n=-\infty}^{\infty} F\left(j \frac{n \pi}{t_{m}}\right) \mathrm{Sa}\left(\omega t_{m}-n \pi\right), \quad t_{m}=\frac{1}{2 f_{s}} F(jω)=n=?∞∑∞?F(jtm?nπ?)Sa(ωtm??nπ),tm?=2fs?1?
频域取样定理用的比较少,了解即可。
《工程信号与系统》作者:郭宝龙等
中国大学MOOC:信号与系统 ,西安电子科技大学,郭宝龙,朱娟娟