??最近在工程实践中,遇到一个数值计算精度丢失与误差传播的问题,折腾了许久。在此,记录下该问题,时刻警惕数值计算过程的精度丢失与误差传播的问题。关于数值计算的四种误差参见博文: 模型误差、观测误差、截断误差(或称方法误差)、舍入误差。
一、问题描述
??现有函数表达式
f
(
x
0
,
x
1
,
x
2
)
=
x
0
2
+
x
1
2
?
x
2
2
f(x_0,x_1,x_2)=x_0^2+x_1^2-x_2^2
f(x0?,x1?,x2?)=x02?+x12??x22?,其中自变量
x
0
,
x
1
,
x
2
x_0,x_1,x_2
x0?,x1?,x2?是根据其他表达式(包含三角函数、平方根函数等)计算而来。发现问题:在不同的平台下
x
0
,
x
1
,
x
2
x_0,x_1,x_2
x0?,x1?,x2?的值略有不同,误差很小,但是计算所得
f
f
f的值却大为不同!
??在平台1上(所计算值存在误差),
x
0
=
?
226300.537317
,
x
1
=
?
728435.474466
,
x
2
=
?
762777.937573
,
f
(
x
0
,
x
1
,
x
2
)
=
?
8397.6499023437500
x_0=-226300.537317,x_1=-728435.474466,x_2=-762777.937573,f(x_0,x_1,x_2)=-8397.6499023437500
x0?=?226300.537317,x1?=?728435.474466,x2?=?762777.937573,f(x0?,x1?,x2?)=?8397.6499023437500。
??在平台2上(可以认为所计算值为精确的),
x
0
=
?
226300.5077347187
,
x
1
=
?
728435.4269486722
,
x
2
=
?
762777.8319934641
,
f
(
x
0
,
x
1
,
x
2
)
=
70054.236328125000
x_0=-226300.5077347187,x_1=-728435.4269486722,x_2=-762777.8319934641,f(x_0,x_1,x_2)=70054.236328125000
x0?=?226300.5077347187,x1?=?728435.4269486722,x2?=?762777.8319934641,f(x0?,x1?,x2?)=70054.236328125000。
??自变量较小的绝对误差与很小的相对误差,经过简单的函数映射后,因变量计算结果竟然差距这么大。失之毫厘,谬以千里。
二、代码实例
#include <stdio.h>
void main(void)
{
double x_[3] = { -226300.537317, -728435.474466, -762777.937573 }; //平台1带误差计算值
double x[3] = { -226300.5077347187, -728435.4269486722, -762777.8319934641 }; //平台2计算值(认为是精确的)
double absoluteErrorX[3], relativeErrorX[3], f_, f, absoluteErrorF, relativeErrorF;
for (int i = 0; i < 3; i++)
{
absoluteErrorX[i] = x_[i] - x[i];
relativeErrorX[i] = absoluteErrorX[i] / x[i];
}
f_ = x_[0] * x_[0] + x_[1] * x_[1] - x_[2] * x_[2];
f = x[0] * x[0] + x[1] * x[1] - x[2] * x[2];
absoluteErrorF = f_ - f;
relativeErrorF = absoluteErrorF / f;
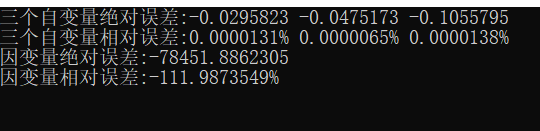
printf("三个自变量绝对误差:%.7f %.7f %.7f\n", absoluteErrorX[0], absoluteErrorX[1], absoluteErrorX[2]);
printf("三个自变量相对误差:%.7f%% %.7f%% %.7f%%\n", relativeErrorX[0] * 100, relativeErrorX[1] * 100, relativeErrorX[2] * 100);
printf("因变量绝对误差:%.7f\n", absoluteErrorF);
printf("因变量相对误差:%.7f%%\n", relativeErrorF * 100);
}