[人工智能]模型纠偏之保序回归

模型纠偏背景

广告系统和推荐系统有个显著的不同，广告模型要求预估值绝对的准确，而推荐模型大部分只要求序一致就行，主要是因为广告的模型设计到计费逻辑，所以需要保证预估绝对值的准确性，模型层面上，可以尽量保证特征、数据样本要做到准确，尽管如此，仍然模型可能存在预估的偏差，那么在模型层面之外，就需要一个更加强有力的纠偏策略，这也是本文介绍的点
reference

本文主要参考

[1]Predicting Good Probabilities With Supervised Learning
[2]ACTIVE SET ALGORITHMS FOR ISOTONIC REGRESSION; A UNIFYING FRAMEWORK
[3]1.15. Isotonic regression

两种纠偏方法

Platt Calibration

对于某个模型输出值f(x)，platt calibration的方法是将f(x)当做输入，再去训练交叉熵模型
?
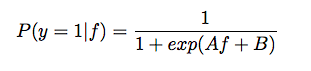
f为原始模型预估值，A和B为训练参数
?
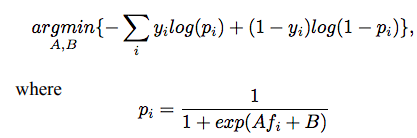
相当于再套了一层模型来做参数调整

保序回归 Isotonic Regression

保序回归问题定义：
这里用sklearn的定义：
?
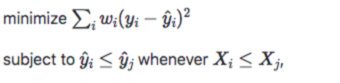
上式 $w_i$ 为样本i的权重，$y_i$ 为样本真实值(实际一般是后验)， $\widehat{y_i}$ 为要求解的值，$x_i$为样本i的模型预估值，需要保证的是对于任意的$x_i\le x_j$都有$\widehat{y_i}\le \widehat{y_j}$ 这也就是保序的由来
保序的场景：在广告系统中，模型预估值会作用到后面的ranking排序，对于一个pv有n条候选，会预估出n个预估值 $x_i$ ，同时会有对应的n个历史统计后验值$y_i$(一般是离线统计存在redis或者其他的存储介质里)，保序回归需要在不能影响模型预估的序的情况下，做到纠偏值 $\widehat{y_i}$ 尽量接近后验$y_i$
求解方法
求解上述问题的方法又多种，这里介绍常见的一种，称之为PAVA的算法(reference[2])，PAV求解步骤如下
?

翻译成人话，举个例子
5个样本，模型 $x_i$ 预估值分别是 0.1 0.2 0.3 0.4 0.5，假设样本 $w_i$ 权重都是1，真实后验 $y_i$ 值是 0.3 0.4 0.2 0.0 0.6，求解步骤如下：

• 对元组$(x_i,y_i)$先按照$x_i$从小到大排序(以增序为例)
• 从 $x_0$ 对应的$y_0$开始，观察其后面的后验值是否大于前面，观察到0.3<0.4是递增序，那么$\widehat{y_i}$=0.3记为第一个 $bloc{k}_0$ ，同时将索引移动到 $x_1$
• 发现0.2<0.4, 则将 $y_1$ 和 $y_2$ 都记为$bloc{k}_1$，计算$block1$的平均值为0.3(如果权重不是1的话，那么计算加权平均值)，再往后面观察，发现0.1仍然小于0.3，那么将0.1 也加到$block1$中，同时重新计算平均值为0.2，继续观察0.2<0.6，则$block1$停止拓展，其预估值为0.2
• 继续移动索引，到0.6，因为是最后一个元素且是新的$block$，则$block3$为0.6
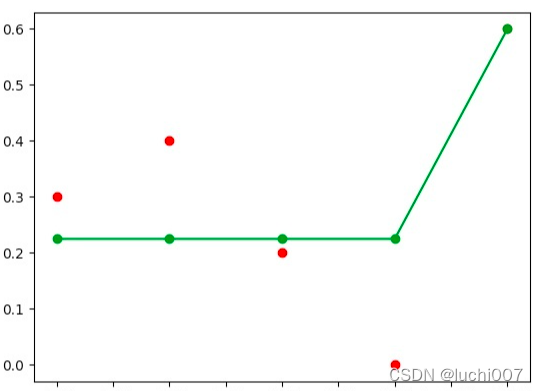
• 现在有3个$block$，每个$block$对应的值为0.3 0.2 0.6，显然仍然需要继续计算，重复上面计算过程最终会得到2个$block$，第一个$block$包含前4个元素，值为0.225，第二个$block$包含一个元素，值为0.6

代码验证一下：

from sklearn.isotonic import IsotonicRegression
from matplotlib.collections import LineCollection
x = [0.1,0.2,0.3,0.4,0.5]
y = [0.3,0.4,0.2,0.0,0.6]
ir = IsotonicRegression()
y_ = ir.fit_transform(x, y)
y_
array([0.225, 0.225, 0.225, 0.225, 0.6 ])
其纠偏图如下
?

最后补充一个比较生动展示纠偏过程的动图，作为总结(图片来自Isotonic Regression，非营利性目的使用，若有侵权，请联系该账号简介中的邮箱，速删 )：
?