梯度下降
在机器学习中,无论是回归还是分类,我们大部分的目标是优化损失函数使其最小,但如何让机器找到使损失函数最小的参数?根据微积分的知识我们知道在函数的极小值点附近,如果沿着函数梯度的方向行走,函数值是下降的:
L
(
w
′
)
<
L
(
w
)
,
w
′
=
w
?
α
?
L
?
w
L(w')<L(w),w'=w-\alpha\frac{\partial{L}}{\partial{w}}
L(w′)<L(w),w′=w?α?w?L?
以线性回归问题为例(如下图),损失函数为二次函数。式中的a为学习率,当学习率较小的时候,权重梯度优化的速度较慢,损失每次变化的幅度较小,收敛到最小值点速度慢。反之学习率较大时,参数每次变化幅度大,可能导致整个优化行为数值不稳定,甚至无法收敛。故在实际任务中选一个合适的学习率比较重要。
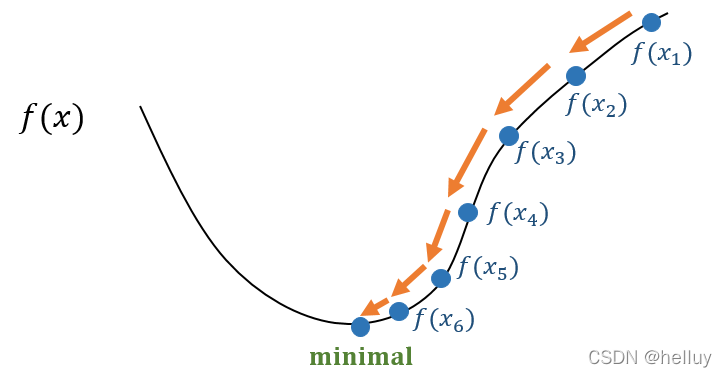
梯度下降思想是深度学习中优化的基本思想,但是标准的梯度下降法很难适用在实际任务,因为每一次执行梯度下降就要计算全部样本的损失,现在的算力无法承担如此大的计算量,故需要对梯度下降法进行优化。常用的方法为以下几个。
随机梯度下降(SGD)
随机梯度下降应用的是统计学中随机抽样的方法,它不对总体直接计算,而是随机抽取样本计算期望对总体做近似估计。标准的梯度下降的损失函数如下:
f
(
x
)
=
1
n
∑
i
=
1
n
l
i
(
x
)
f(x)=\frac{1}{n}\sum_{i=1}^{n}{l_i(x)}
f(x)=n1?i=1∑n?li?(x)
其中li(x)表示每个样本的损失,f(x)就是在时间t上的总损失。
随机梯度下降则在时间t不计算全部的样本损失,而是随机抽取一个样本ti的损失来近似全部损失f(x):
x
t
=
x
t
?
1
?
α
t
?
l
i
?
x
t
?
1
x_t=x_{t-1}-\alpha_{t}\frac{\partial{l_i}}{\partial{x_{t-1}}}
xt?=xt?1??αt??xt?1??li??
其中xt,xt-1表示t、t-1时刻的参数,at为t时刻的学习率。
为什么可以这么做?因为统计学中,随机样本期望等于总体的期望(例如我在总体中随机抽取4个样本计算期望与总体的期望不会太大,在大量的样本抽取中可以近似替代),所以在这里随机抽取一个样本的情况下:
E
[
?
l
i
(
x
)
]
=
E
[
?
f
(
x
)
]
E[\nabla l_i(x)]=E[\nabla f(x)]
E[?li?(x)]=E[?f(x)]这里的等号不是严格等于,而是近似替代。
随机梯度下降的好处就是我可以每次参数更新时算一个样本的损失,求出梯度来梯度更新,极大的减少了耗费的资源。
小批量随机梯度下降
从上述知道标准的随机梯度下降是每次抽取一个样本,不是很稳定(具有高方差),而且直接从全部样本变成了1个,导致完全不耗费算力(有点像优化过头了),所以提出了小批量随机梯度下降:在时间t上抽取b个样本(就是深度学习中的batchsize),通过计算这b个样本的梯度的平均来逼近f(x)。
x
t
=
x
t
?
1
?
α
t
b
∑
i
∈
I
t
?
l
i
(
x
t
?
1
)
=
x
t
?
1
?
α
t
b
∑
i
∈
I
t
?
l
i
?
x
t
?
1
x_t=x_{t-1}-\frac{\alpha_{t}}{b}\sum_{i\in I_t}\nabla l_i(x_{t-1})=x_{t-1}-\frac{\alpha_{t}}{b}\sum_{i\in I_t}\frac{\partial{l_i}}{\partial{x_{t-1}}}
xt?=xt?1??bαt??i∈It?∑??li?(xt?1?)=xt?1??bαt??i∈It?∑??xt?1??li??
其中It表示含有b个样本的集合,x是参数。
与随机梯度下降的思想相同,这也是一个无偏估计,但比标准的随机梯度下降具有更小的方差。
冲量法(momentum)
在实际任务中,面对的损失函数往往十分不平滑,如果根据梯度的方向来更新权重会导致不稳定(因为这一时刻的梯度方向往往与上一时刻完全相反),而且还有个问题:容易陷入局部最小。所以可以引入一个冲量使梯度的更新方向不会完全依赖当前梯度的方向,而是还要考虑之前的梯度方向,通俗点说就是类比于一个人跑步不会立马停下还会有惯性使他继续向前跑一段距离。这样有利于越过一些极大值点找到全局极大值。
g
t
=
1
b
∑
i
∈
I
t
?
l
i
(
x
t
?
1
)
g_t=\frac{1}{b}\sum_{i\in I_t}{\nabla l_i(x_{t-1})}
gt?=b1?i∈It?∑??li?(xt?1?)
与小批量随机梯度下降一样,gt表示t时刻的近似梯度。但是冲量法并不以该梯度更新参数,而是以vt:
v
t
=
β
v
t
?
1
+
g
t
v_t=\beta v_{t-1}+g_t
vt?=βvt?1?+gt?
w
t
=
w
t
?
1
?
α
v
t
w_t=w_{t-1}-\alpha v_t
wt?=wt?1??αvt?
其中
β
\beta
β是个小于1大于0的数,由vt的递推式可以看到,vt综合了之前的梯度(gt,gt-1,…,g1),使得在wt参数更新时考虑之前的梯度更新方向,而且时间与t时刻越近,对当前的梯度更新影响越大。
v
t
=
g
t
+
β
g
t
?
1
+
β
2
g
t
?
2
+
.
.
.
+
β
n
?
1
g
1
v_t=g_t+ \beta g_{t-1}+{\beta}^2g_{t-2}+ ... + {\beta}^{n-1}g_1
vt?=gt?+βgt?1?+β2gt?2?+...+βn?1g1?
当
β
\beta
β为0时,冲量法等同于小批量随机梯度下降。
Adam
Adam是另一种优化算法,它相较于SGD对学习率没那么敏感,也是实际任务中最常用的方法之一。
它的权重更新公式如下:
先记录两个变量vt,st:
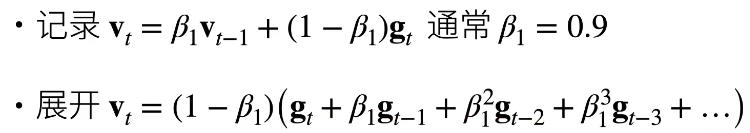
当t值较小时,beta的等比级数的和不为1,所以将vt修正为一下形式:


然后进行参数更新:

参考资料:
https://zhuanlan.zhihu.com/p/36564434
李沐–动手学深度学习v2
深度学习笔记 2022/02/26