神经网络中的激活函数与损失函数&深入理解softmax交叉熵
前面在深度学习入门笔记1和深度学习入门笔记2中已经介绍了激活函数和损失函数,这里做一些补充,主要是介绍softmax交叉熵损失函数。
激活函数
sigmoid函数
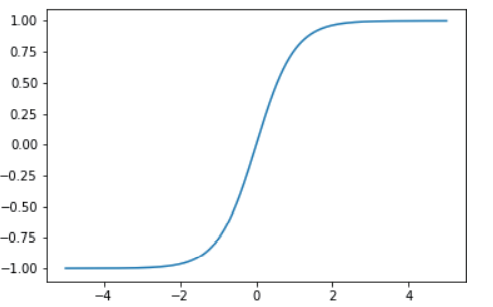
神经网络中经常使用的一个激活函数就是sigmoid函数。
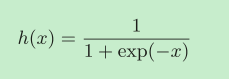
它的图像是:
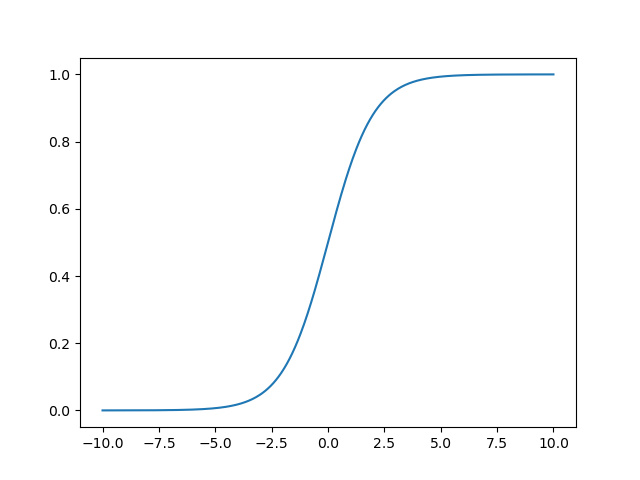
sigmoid函数常用于回归问题。
softmax函数
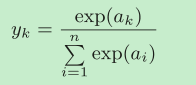
softmax函数的分子是输入信号ak的指数函数,分母是所有输入信号的指数函数的和。
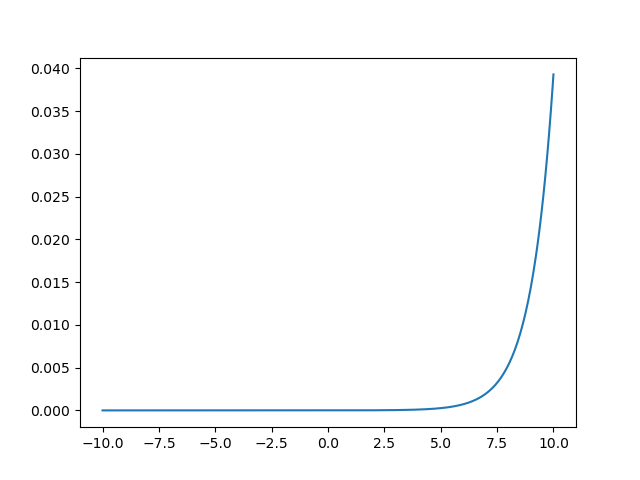
softmax函数的输出是0.0到1.0之间的实数。并且,softmax函数的输出值的总和是1,这是softmax函数的一个重要性质。正因为有了这个性质,我们才可以把softmax函数的输出解释为“概率”。
从softmax的名字来看,就知道应该有一个与之对应的hardmax,其实hardmax就是直接简单粗暴地选择一个最大值,而softmax则将所有的结果以概率的形式输出。
softmax函数的优缺点
优点是它既能产生更陡峭的梯度,又具有一些优雅的数学属性。
- 这里“更陡峭的梯度”在神经网络的学习中很重要,sigmoid函数在这方面就表现地不是很好:sigmoid函数曲线相对平坦的梯度,sigmoid函数的最大斜率是0.25,所以当把这些梯度向后发送至模型中的上一个运算时,这些梯度最多只能除以4而更糟糕的是,当 sigmoid 函数的输入小于–2或大于2时,这些输入所接收的梯度将几乎为0,这是因为 sigmoid(x) 在 x = –2 或 x = 2 时几乎是平坦的。这意味着影响这些输入的任何参数都会收到较小的梯度,因此神经网络的学习速度会很慢(在使用梯度下降法SGD时,修改参数值,然后继续观察反向传播回来的梯度,然而因为sigmoid函数近乎平坦的曲线,反向传播回来的梯度几乎没有什么变化,这就意味着要进行多次的梯度下降才能看到效果)
sigmiod函数的导数图像如下:
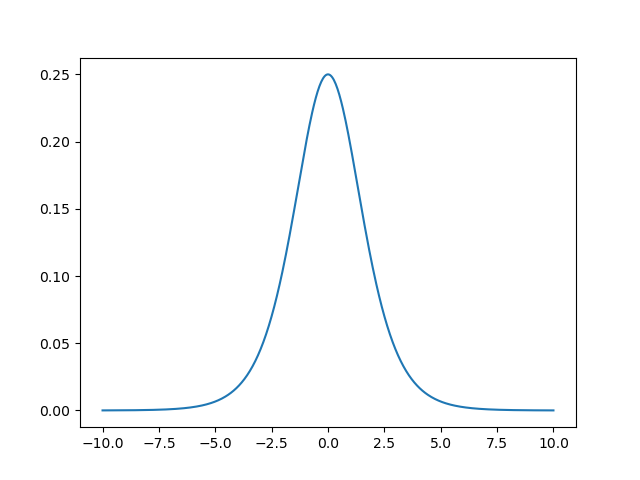
- 这里“优雅的数学属性”后面结合交叉熵损失函数一起说明。
缺点是溢出问题。softmax函数的实现中要进行指数函数的运算,但是此时指数函数的值很容易变得非常大。比如,e10的值 会超过20000,e100会变成一个后面有40多个0的超大值,e1000的结果会返回 一个表示无穷大的inf。如果在这些超大值之间进行除法运算,结果会出现“不确定”的情况。
一般情况下我们会采取将所有的输入值减去输入值中的最大值,然后再进行运算。
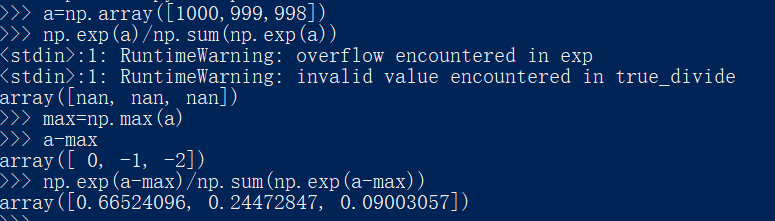
这么做会不会有问题呢?不会的,这是因为在进行softmax的指数函数的运算时,加上(或者减去) 某个常数并不会改变运算的结果。
ReLU函数
ReLU函数非常简单,如果 x 小于 0,则 ReLU 简单地定义为 0,否则定义为 x。
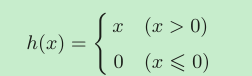
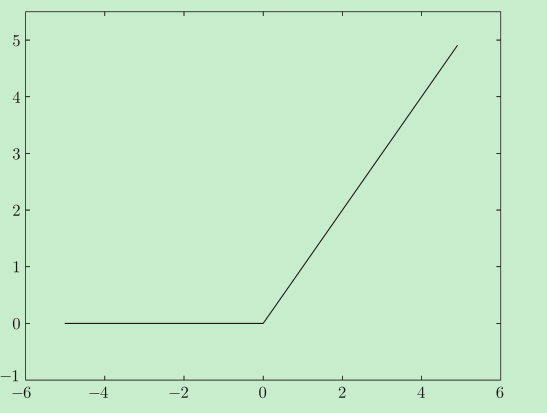
从单调和非线性的角度来看,这是一个“有效”的激活函数。它产生的梯度要比 sigmoid 函数大得多,函数的输入大于0,则梯度为1,其他情况则为0,平均梯度为0.5。ReLU 激活函数在深度神经网络架构中是非常 流行的选择,这是因为它的缺点(在小于 0 和大于 0 的值之间形成了过于明显的差别)可 以通过其他技术来弥补。
ReLU有一些变体:当 ReLU 激活函数的输入小于 0 时,Leaky ReLU7 激活函数允许略微的负斜率,从而增强 ReLU 激活函数向后发送梯度的能力。不过从简单和易于计算两个方面考虑,ReLU足够应付很多简单的场景。
Tanh函数
Tanh函数介于sigmoid和ReLU 之间,是一种折中方案,它的形状与 sigmoid 函数类似,但输出的取值范围是 –1 ~ 1。
它产生比 sigmoid 曲线更陡峭的梯度:
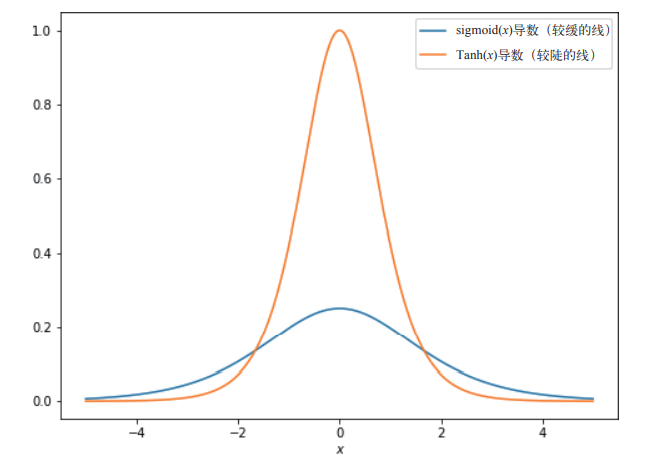
f=sigmoid(x)和f=Tanh(x)都有着方便计算的导数: f`=sigmoid(x)*(1-sigmoid(x)) 和 f`=1-Tanh2(x) 。
损失函数
神经网络的学习需要通过某个指标表示现在模型的状态,然后以这个指标为基准,寻找最优权重参数。这个指标称为损失函数(loss function)。这个损失函数可以使用任意函数,但一般用均方误差和交叉熵误差等。
之前的文章中提到了为什么不适用“准确率”这样简单的指标,因为“准确率”是离散的,不连续的,没有办法使用梯度来寻找最优权重参数。
损失函数是表示神经网络性能的“恶劣程度”的指标,即当前的神经网络对监督数据在多大程度上不拟合,在多大程度上不一致。
MSE均方误差
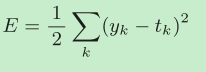
yk是表示神经网络的输出,tk表示监督数据,k表示数据的维数。
交叉熵误差
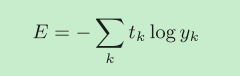
yk是神经网络的输出,tk是正确解标签。并且,tk中只有正确解标签的索引为1,其他均为0,也就是进行了独热编码(one-hot encoding)。
softmax交叉熵
交叉熵函数和softmax激活函数常常合在一起使用,称为Softmax-with-Loss。
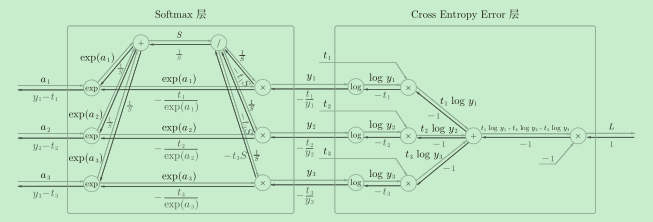
二者一旦结合,就会出现“魔术”般的效果:可以看到,Softmax层的反向传播得到了(y1?t1, y2?t2, y3?t3)这样“漂亮”的结果,这也是softmax函数所谓的“优雅的数学属性”。在tensorflow库中,一般也推荐使用统一的接口,而不是单独使用Softmax函数与交叉熵损失函数。
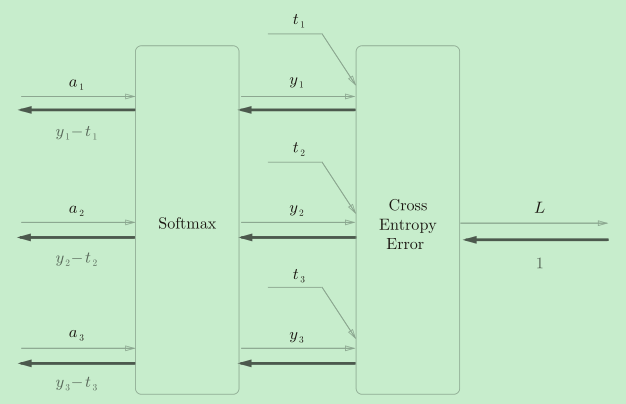
softmax交叉熵的计算图推导过程
](https://img-blog.csdnimg.cn/img_convert/62bf4bec7ba506ce84934cdf9f213335.png)
softmax交叉熵的计算图推导过程
