[人工智能]聚类分析(CA)

聚类分析

1 概念

聚类分析又称群分析，是根据“物以类聚”的道理，对样本或指标进行分类的一种多元统计分析方法，它讨论的对象是大量的样本，要求能合理地按照各自的特性来进行合理的分类，没有任何模式可供参考或依循，即在没有先验知识的情况下进行的。

• 聚类分析----无监督学习方法
• 聚类是为了更好地分类

2 两种类型

在实际问题中，收集n个样本，对每一个样本测量p个指标/变量：

• Q型聚类
  • 根据p个指标对n个样本进行分类
  • 如：根据多项经济指标（指标）对不同的地区（样本）进行分类
• R型聚类
  • 根据n个样本对p个指标进行分类
  • 如：根据不同地区的样本数据（样本）对多项经济指标（指标）进行分类

【注：两者没有本质区别，实践中人们更感兴趣的通常是Q型聚类】

3 相似性度量

3.1 样本间的相似性度量

• 距离--->样本间的相似性度量

【注：最常用的是闵氏距离中的欧氏距离，需先进行数据标准化处理得到相同量纲的变量，然后再计算距离】

3.2 指标间的相似性度量

• 相似系数--->指标间的相似性度量

【注：最常用的是皮尔逊相关系数(协方差)】

3.3 类间的相似性度量

• 距离--->类间的相似性度量

1. 最短距离法
   • 以两类中距离最近的两个样本之间的距离作为类间距离
   • 
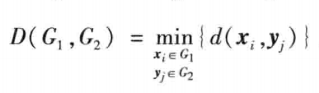
2. 最长距离法
   • 以两类中距离最远的两个样本之间的距离作为类间距离
   • 
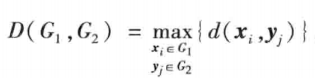
3. 重心法
   • 以两类变量均值之间的距离作为类间距离
   • 
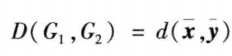
4. 类平均法
   • 以两类样本两两之间距离的平均数作为类间距离
   • 
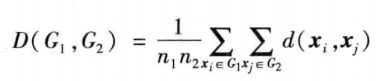
5. 离差平方和法
   • 先将n个样本各自归成一类，然后每次减少一类，随着类与类的不断聚合，类内离差平方和必然不断增大，选择使离差平方和增加最小的两类合并，直到所有的样本归为一类为止
   • 

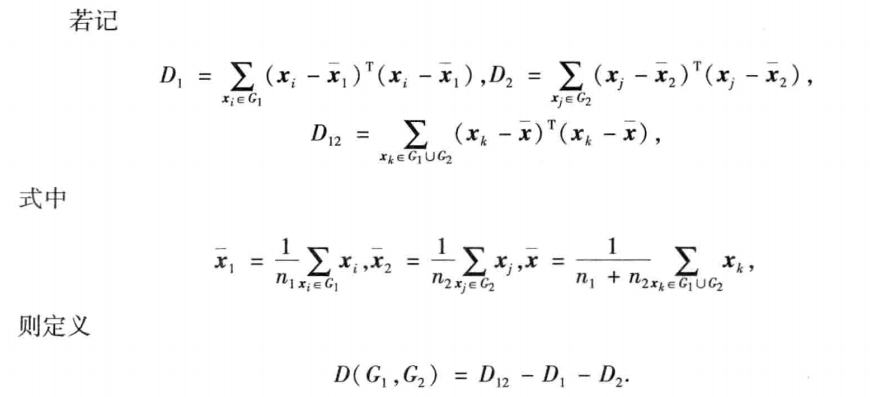
【注：最常用的是类平均法和离差平方和法】

4 系统聚类法

4.1 基本思想

逐步将距离近的类合并在一起

先将所有n个样本看成不同的n类，然后将性质最接近（距离最近）的两类合并为一类；再从这n-1类中找到最接近的两类加以合并，以此类推，直到所有的样本被合为一类

【这种系统归类过程与计算类和类之间的距离有关，采用不同的距离定义。有可能得出不同的聚类结果】

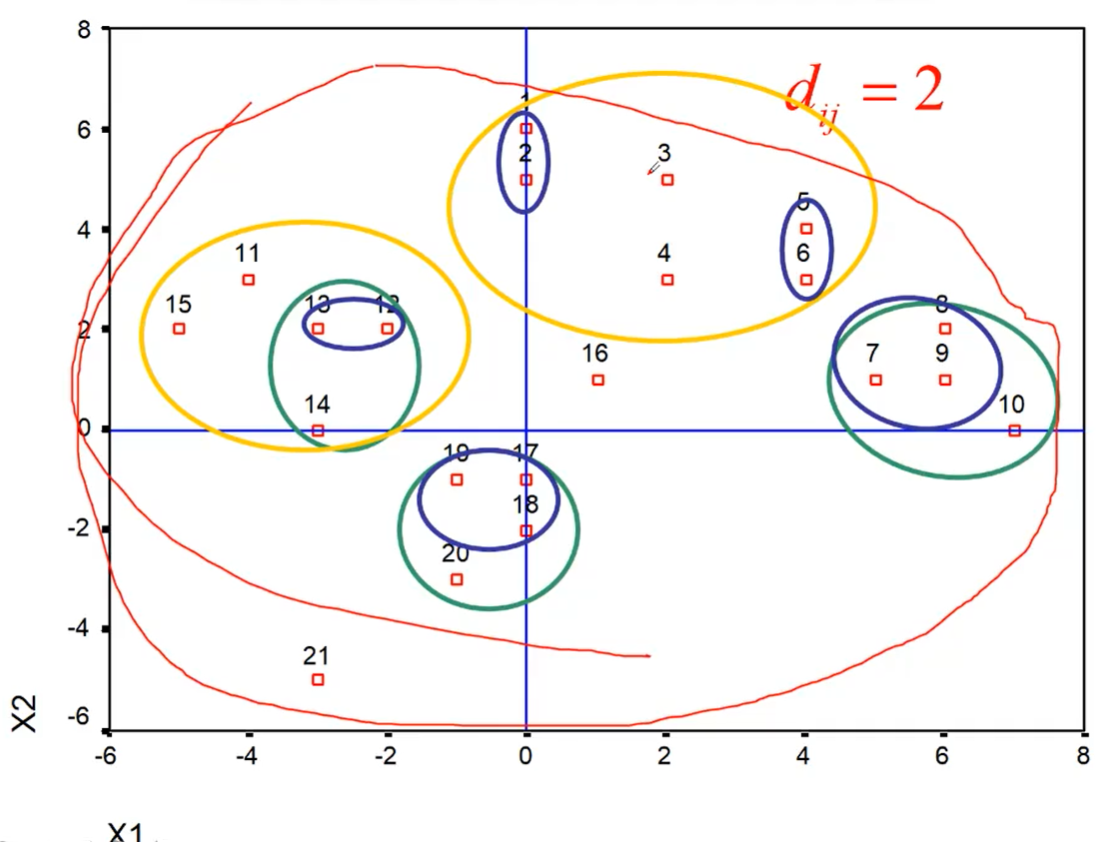
4.2 步骤

4.3 最短距离法

若使用最短距离法来测量类与类之间的距离，即称其为系统聚类法中的最短距离法

4.4 类平均法

4.5 离差平方和法

4.6 优缺点

• 优点：
  • 事先不需要确定要分多少类
  • 聚类过程一层层进行，最后得出所有可能的类别结果，研究者根据具体情况确定最后需要的类别
  • 该方法可以绘制出树状聚类图，方便使用者直观选择类别
• 缺点：
  • 计算量较大，对大批量数据的聚类效率不高
  • 当每个观测值被归属在某一类中，纵使后来发现不恰当，也不会被重新归属

5 SPSS系统聚类法实例

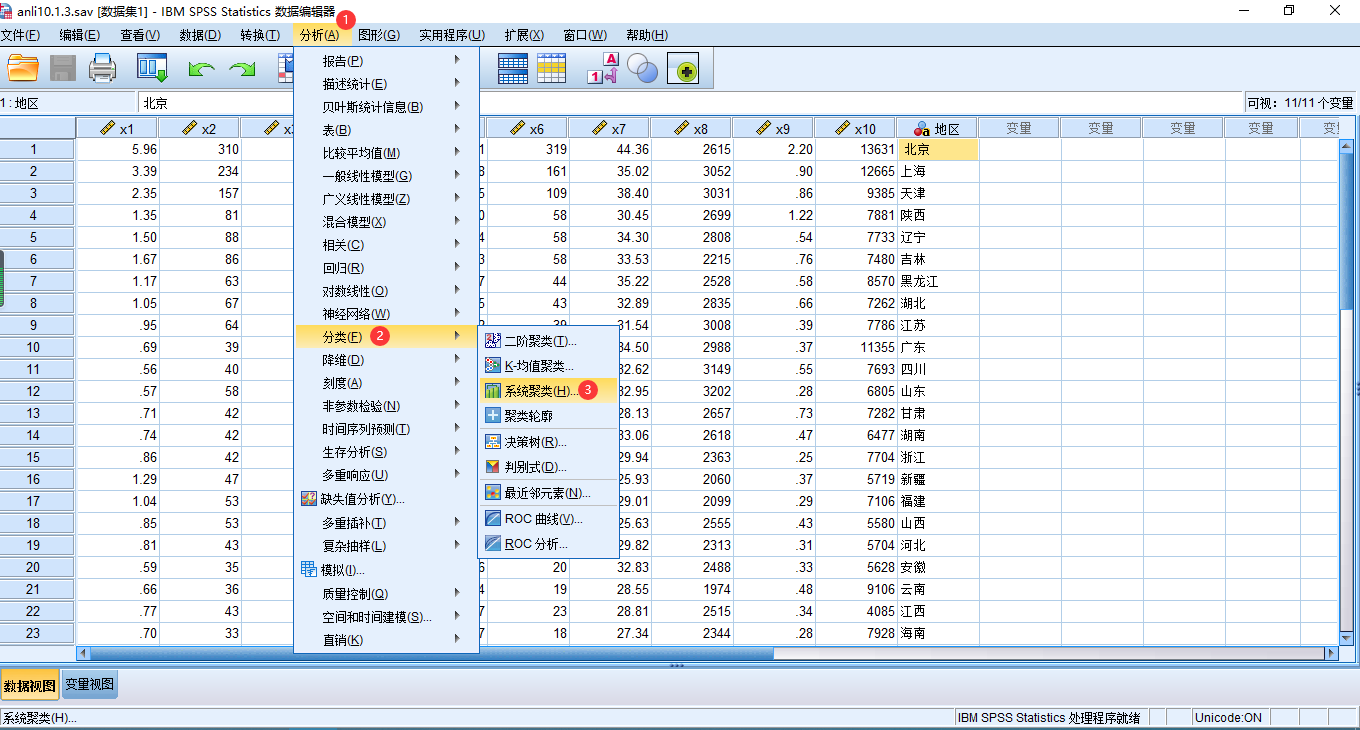
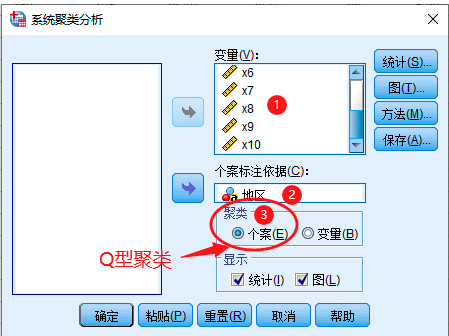
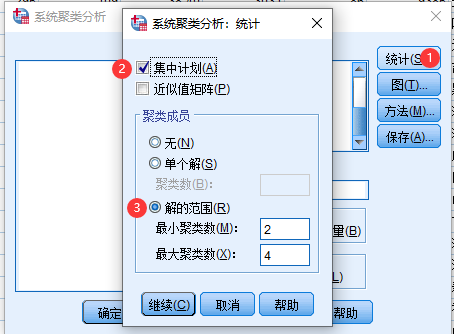
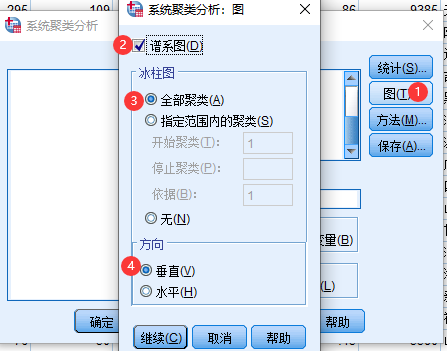
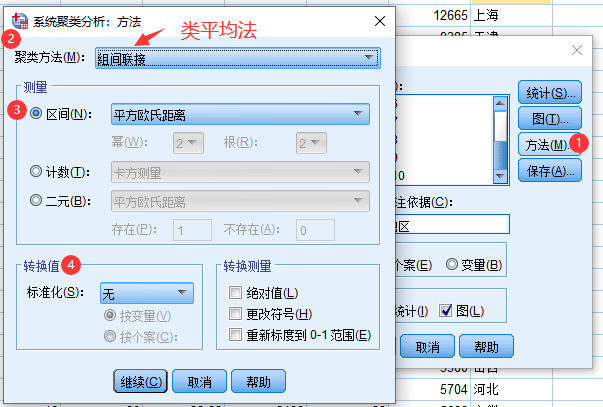
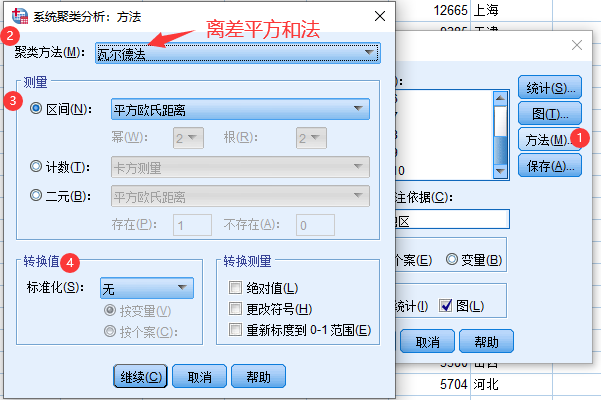
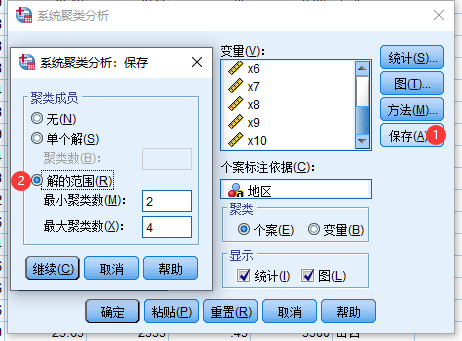
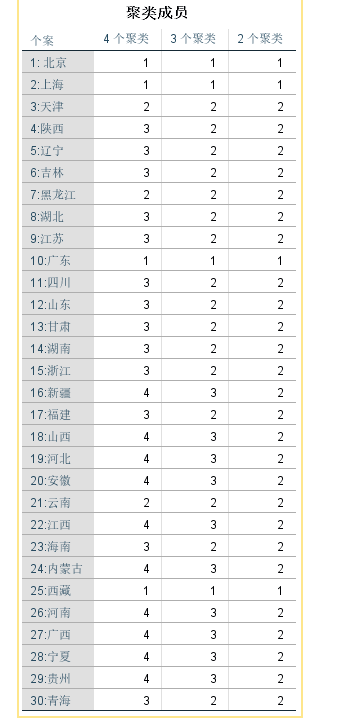
6 Matlab系统聚类法实例

• R型聚类分析

  %% I.R型聚类分析【根据不同地区对多项指标进行分类-->从10个指标中选定了6个分析指标】
  clc,clear
  close all
  a=load('gj.txt')    							% 读取导入纯文本文件gj.txt
  b=zscore(a) 									% 数据标准化
  r=corrcoef(b)   								% 计算相关系数矩阵
  % % 另外一种计算距离方法
  % d=tril(1-r)
  % d=nonzeros(d)'
  d=pdist(b','correlation')   					% 计算相关系数导出的距离
  z=linkage(d,'average')  						% 按类平均法聚类
  h=dendrogram(z) 								% 画聚类图
  set(h,'color','k','LineWidth',1.3)   			% 把聚类图线的颜色改成黑色，线宽加粗
  T=cluster(z,'maxclust',6)   					% 把变量划分成6类
  for i=1:6
      tm=find(T==i)   							% 求第i类的对象
      tm=reshape(tm,1,length(tm))					% 变成行向量
      fprintf('第%d类的有%s\n',i,int2str(tm))		 % 显示分类结果
  end
  

• Q型聚类分析

  %% II.Q型聚类分析【根据多项指标对不同地区进行分类-->从6个分析指标对30个地区进行聚类分析】
  clc,clear
  close all
  load gj.txt 									% 读取导入数据矩阵
  gj(:,[3:6])=[] 						% 删除数据矩阵的第3~6列，即使用变量1,2,7,8,9,10【6项指标】
  gj=zscore(gj) 									% 数据标准化
  y=pdist(gj) 									% 求对象间的欧氏距离，每行是一个对象
  z=linkage(y,'average')  						% 按类平均法聚类
  h=dendrogram(z) 						 		% 画聚类图
  set(h,'color','k','LineWidth',1.3) 				% 把聚类图线的颜色改成黑色，线宽加粗
  for k=3:5
      fprintf('划分成%d类的结果如下:\n',k)
      T=cluster(z,'maxclust',k)   				% 把样本点划分成k类
      for i=1:k
          tm=find(T==i)   						% 求第i类的对象
          tm=reshape(tm,1,length(tm))   			% 变成行向量
          fprintf('第%d类的有%s\n',i,int2str(tm))  % 显示分类结果
      end
      if k==5
          break
      end
      fprintf('**************************************************\n')
  end