[人工智能]Large Scale Image Completion via Co-Modulated Generative Adversarial Networks解读

题目：Large Scale Image Completion via Co-Modulated Generative Adversarial Networks（通过协同调制生成对抗网络进行大规模图像填充）

这篇论文主要针对大部分补全网络对于具有大面积掩码的图像的补全存在一定的局限性。提出自己的论点：作者认为，要克服这一问题，关键是协调有条件的图片生成框架和无条件的图片生成网络框架间的差异。

CO-MODULATED GENERATIVE ADVERSARIAL NETWORKS(协同生成对抗器网络)

我们假设，在训练数据中，输入条件和输出图像之间的配对对应关系是可用的。生成器将一个图像$y$和潜在向量$z$作为输入，并产生输出$x$；鉴别器以一对$(x,y)$作为输入，并试图从真实分布中区分假生成的对。图像补全可以看作是一个受约束的图像条件生成问题，其中已知的像素被限制为不变的。与大量关于专门的图像补全框架的文献相比，我们提出了协调图片有条件生成对抗网络和近期成功的无条件调制框架的通用方法。

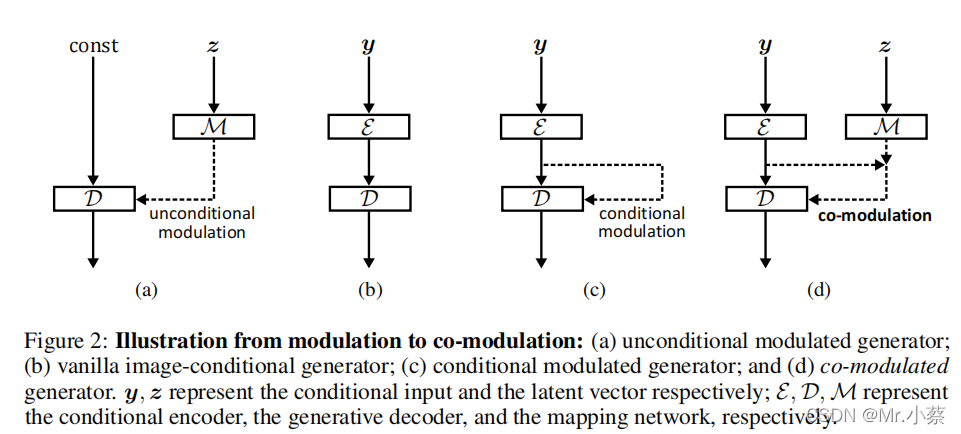
REVISITING MODULATION APPROACHES （回顾调制方法）

作者主要介绍了两种调制方式：无条件调制生成器和条件调制生成器。无条件调制器以StyleGAN2为例，展示中间激活时如何作为潜在载体函数被调节的。如Fig 2(a)所示，解码器$D$仅仅来源于一个训练学习得到的常量，而潜在向量z则是通过一个多层全连接映射网络$M$ 。映射的潜在向量通过学习到的仿射变换$A$（即一个没有激活的密集层）为每个后续调制线性生成一个样式向量$s$。
$$s=A(M(z))$$
考虑到一个具有核权值$w_{ijk}$的普通卷积层，其中$i、j、k$分别代表输入通道、输出通道以及卷积核的大小。给定样式向量$s$，输入的特征映射首先按通道方向乘以$s$，通过卷积，最后按通道乘以$s^{\prim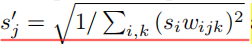e }$其中
作为权重解调步骤，将特征映射归一化为统计上的单位方差。
虽然调制方法已经显著提高了无条件或类条件生成器的性能，但我们想知道它们是否也可以类似地用于图像条件生成器。对普通的图像条件生成器(Fig.2(b))的一个直观的扩展将是条件调制生成器(Fig.2?)，其中，调制是基于从图像编码器$\xi$学到的扁平特征。在本例中，样式向量可以重写为:
$$s=A(\xi (y))$$
然而，条件调制方法的一个显著缺点是缺乏随机生成能力。

CO-MODULATION

为了克服这一挑战，我们提出了共调制，这是一种通用的新方法，可以轻松地将生成能力从无条件调制生成器调整到图像条件生成器。我们将共调制样式向量改写为（见图2(d)）：
$$s=A(\xi (y),M(z))$$
即，对两种样式表示的联合仿射变换。一般来说，样式向量可以是来自两个输入的非线性学习映射，但是这里我们简单地假设它们可以在样式空间中线性相关，并且已经观察到相当大的改进。线性相关促进了内在的随机性，这将在5.1节中看到。共调制的GANs可以很容易地权衡质量和内部条件下地多样性，而不造成任何外部损失，而且共调制不仅有助于随机性，而且有助于视觉质量，特别是在大规模的缺失区域。
共调制对抗生成网络采用常规的鉴别器训练损失，同时不需要类似$L1$项的直接指导，以充分利用其随机生成能力。
共调制对抗生成网络的本质是随机的，即它能自然地学习利用随机风格表示而不施加任何外部损失，即使输入图像和输入掩膜都是固定的，他们也能产生不同的结果。

类似博客：https://www.zhihu.com/question/358119398