隐马尔科夫模型
前言
隐马尔科夫模型(HMM)是在马尔科夫链上的一个扩展,属于机器学习,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析
一、定义
隐状态集合:Q={q1,q2,…,qN}
可观测态集合:V={v1,v2,…,vN}
状态序列:I={i1,i2,…,iN}
观察态序列:O={o1,o2,…,oN}
状态转移矩阵:A=[aij]N*N ,其中aij=P(it+1=qj|it=qi)
观测状态生成矩阵:B=[bj(k)]N*M ,其中bj(k)=P(ot=vk|it=qt)
隐状态初始概率分布:Π=[π(i)]N ,其中π(i)=P(i1=qi)
由上得到HMM模型:λ=(A,B,Π)
二、三个基本问题
1、观测序列概率
已知λ=(A,B,Π),O={o1,o2,…,oN}时,计算P(O|λ)的值。
穷举法
在该模型下,计算观测矩阵的概率,因此我们需要计算所有隐状态条件下的结果。既:
P(O|λ)=∑P(O|I,λ),
同时:
P(O|I,λ)=P(I|λ)P(O|I,λ),
其中:
P(I|λ)=πi1ai1i2ai2i3…aiT-1,iT
P(O|I,λ)=bi1(o1)bi2(o2)…biT(oT)
缺点:复杂度较大
前向后向算法
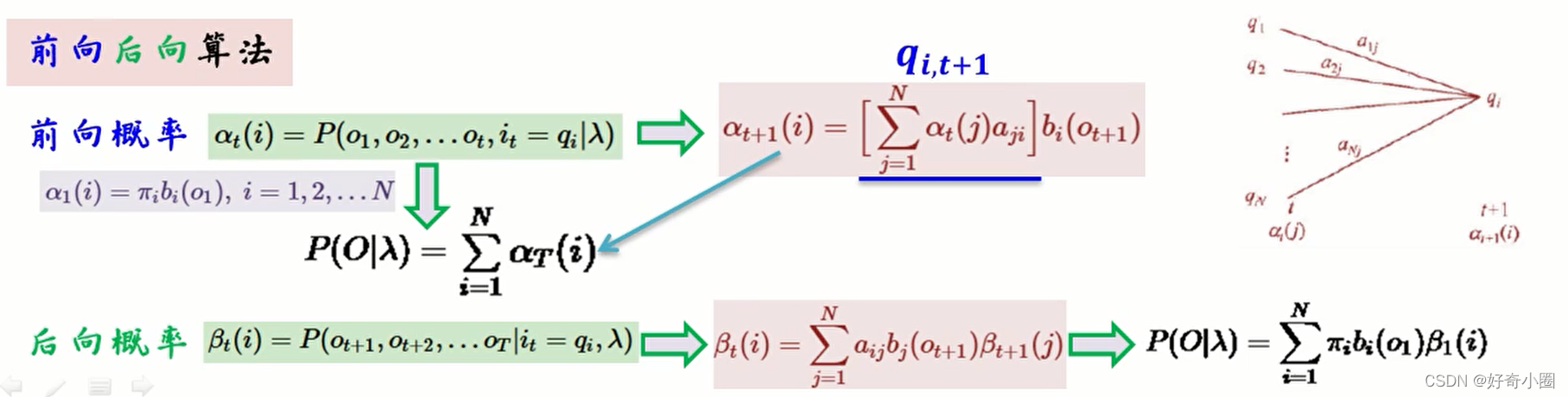
案例
案例来源
三个盒子,各有一定数量的红球白球
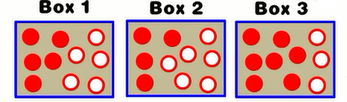
由此可以得到两个集合:

以及模型:

其中A:上一步在某个盒子拿,这一步拿各个盒子的概率
B:当拿某个盒子时,拿到红球、白球的概率
Π:初始拿各个盒子的概率
假设观测序列为O={红,白,红}

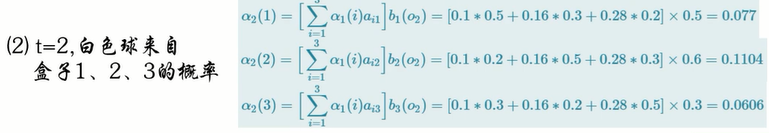

求得最终结果:
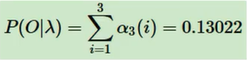
2、模型参数学习
已知O={o1,o2,…,oN}时,求λ=(A,B,Π)
利用期望最大值算法(Expectation-Maximum)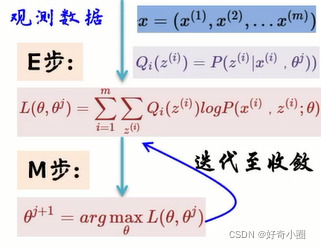

对π求估计:
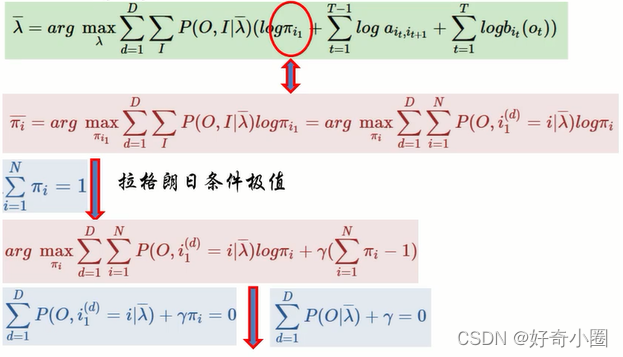
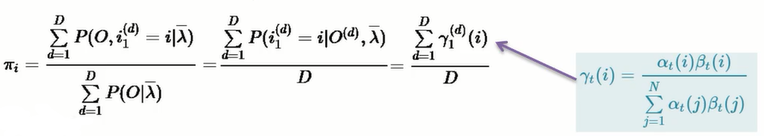

对a和b求估计:

a的分子部分表示在O,λ已知时,该时刻处于隐状态i,并且下一时刻处于隐状态j的概率

3、预测(解码)问题
已知λ=(A,B,Π),O={o1,o2,…,oN}时,求I={i1,i2,……,iN}

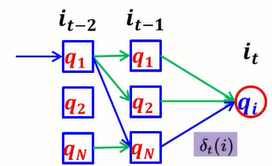
δ既寻找到当前状态最大概率的一个路径。
Φ既在时刻t的时候,隐藏状态为i的,所有状态转移矩阵中,概率最大的那个转移路径中,第t-1个结点的隐藏状态。
接下来不断迭代:
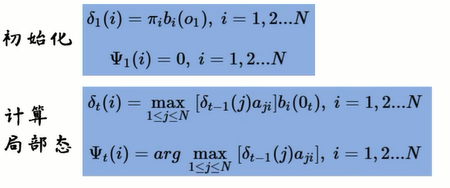
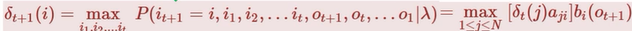
最终得到最可能隐藏序列出现的概率
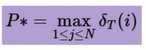
时刻T最可能的隐藏状态
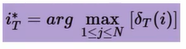
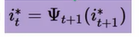
就可以得到最终结果:最可能隐藏态序列

三、三个问题的代码
1、观测序列概率
依然以上述的小球和小盒模型为例,但是观察态序列包含五次观察结果,观测序列为白、红、红、白、白,结果P=0.0212
clear;clc;
box1=[0,0,0,0,0,1,1,1,1,1];%0表示红色,1表示白色
box2=[0,0,0,0,1,1,1,1,1,1];
box3=[0,0,0,0,0,0,0,1,1,1];
boxall=[box1;box2;box3];
O=[];
for i=1:5
O=[O boxall(randi(30))];%生成观察态序列
end
%问题一
A=[0.5,0.2,0.3;0.3,0.5,0.2;0.2,0.3,0.5];%状态转移矩阵
B=[0.5,0.5;0.4,0.6;0.7,0.3];%观测状态生成矩阵
a=zeros(3,5);
pai=[0.2,0.2,0.4];
B_flag=1;%用于切换B的列数
if O(1)==0
B_flag=1;
else
B_flag=2;
end
a(:,1)=pai'.*B(:,B_flag);
for i=2:5
if O(i)==0
B_flag=1;
else
B_flag=2;
end
a(:,i)=(a(:,i-1)'*A)'.*B(:,B_flag);
end
p=sum(a(:,5));
2、模型参数学习
在已知I和O时,可以用监督学习的方法实现:
clear;clc;
box1=[0,0,0,0,0,1,1,1,1,1];%0表示红色,1表示白色
box2=[0,0,0,0,1,1,1,1,1,1];
box3=[0,0,0,0,0,0,0,1,1,1];
boxall=[box1;box2;box3];
O=[];
I=[];
A=zeros(3,3);
B=zeros(3,2);
pai=zeros(1,3);
for i=1:30
temp=randi(30);
I=[I floor((temp-1)/10)+1];
O=[O boxall(temp)];%生成观察态序列
end
%问题2监督学习法
j=1;
for i=2:30
A(I(j),I(i))=A(I(j),I(i))+1;
j=i;
end
A=A/29;
pai=[sum(sign(I==1))/30 sum(sign(I==2))/30 sum(sign(I==3))/30];
for i=1:30
B(I(i),O(i)+1)=B(I(i),O(i)+1)+1;
end
B=B/30;
在未知I时,利用极大似然的方法实现
clear;clc;
A=[0.5,0.2,0.3;0.3,0.5,0.2;0.2,0.3,0.5];%状态转移矩阵
B=[0.5,0.5;0.4,0.6;0.7,0.3];%观测状态生成矩阵
initial=3;%初始状态
seq_len=100;%观察态序列长度
O= zeros(1,seq_len);
curr_state = initial;
for i = 1:seq_len
O(i) = draw(B(curr_state,:));
next_state = draw(A(curr_state,:));
curr_state=next_state;
end
%问题2极大似然法
[newA,newB] = hmmtrain({O},A,B);%自己写的bug多多干脆用MATLAB自带的了
function index = draw(probabilities)
%根据概率向量选择一个类
N = 1000;
P = cumsum(probabilities);
P = round([0 P]*N);
I = zeros(1,N);
for i = 1:length(probabilities)
I(P(i)+1:P(i+1)) = i;
end
%混合向量
I = I(randperm(N));
index = I(1);
end