[人工智能][2107] CSWin Transformer: A General Vision Transformer Backbone with Cross-Shaped Windows

paper
code

Contribution

• propose Cross-Shape Window (CSWin) self-attention
• propose Locally-enhanced Position Encoding (LePE)

Method

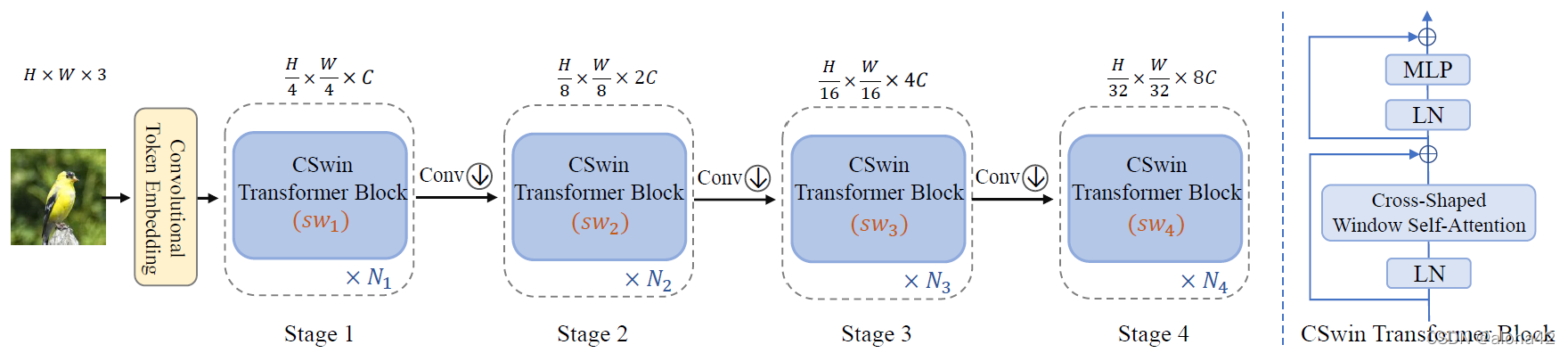
model architecture

Left: the overall hierarchical architecture of our proposed CSWin Transformer, Right: the illustration of our proposed CSWin Transformer block.

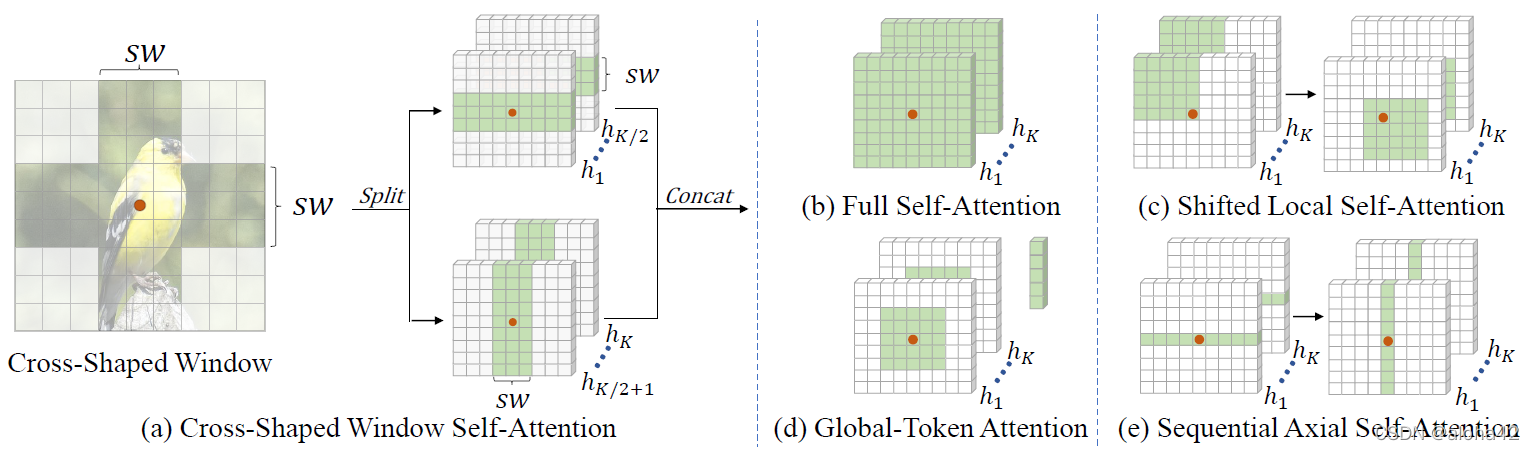
cross-shape window (CSWin) attention

tokens within Transformer blocks limit attention area and require stacking more blocks to achieve global receptive field
solution apply halo (HaloNet) or shifted window (Swin) to enlarge receptive field
an efficient way cross-shaped window self-attention with horizontal and vertical stripes in parallel

(a) Left: the illustration of the Cross-Shaped Window (CSWin) with stripe width sw for the query point(red dot). Right: the computing of CSWin self-attention, where multi-heads ({$h_1,...,h_K$}) is first split into two groups, then two groups of heads perform self-attention in horizontal and vertical stripes respectively, and finally are concatenated together. (b), ?, (d), and (e) are existing self-attention mechanisms.

given input feature $x\in R^{h\times w\times C}$ linearly projected to K heads, which equally split into 2 parallel groups
each head in 2 groups perform locally self-attention within either horizontal or vertical stripes
x evenly partitioned into horizontal stripes, each with $sw\times W$ tokens
$$x=[x_1,x_2,...,x_m]$$
where, $x_i\in R^{sw\times h\times C}$, $m=\frac{h}{sw}$
calculate self-attention for each k-th head
$${y_k}^i=WMSA(x_i{W_k}^Q,x_i{W_k}^K,x_i{W_k}^V),i=1,...,m$$
$${HCS?WMSA}_k(X)=[{y_k}^1,{y_k}^2,...,{y_k}^M]$$
where, $W_k\in R^{C\times C}$ is projection matrix that project self-attention results into target output dimension
similarily, for vertical stripes, attention denoted as ${VCS?WMSA}_k(x)$

concat horizontal and vertical attention output together
$$CS?WMSA(x)=concat(hea{d}_1,...,hea{d}_k)W$$
where, $hea{d}_k=?\begin{array}{rl}{HCS?WMSA}_k(x)& ,k=1,...,\frac{K}{2}\\ {VCS?WMSA}_k(x)& ,k=\frac{k}{2}+1,...,K\end{array}$

adjusted sw small sw for early stages, larger sw for later stages
for HR inputs, h w larger than C in early stages and smaller than C in later stages

1. in early stages (h w larger), smaller sw reduce computation, for local attention
2. in later stages (h w smaller), larger sw enlarge receptive field, for global attention

CSWin transformer encoder

with encoder blocks containing cross-shaped-WMSA, transformer encoder computed as
$$\begin{array}{rl}{z}_l& =CS?WMSA(LN(z_{l?1}))+z_{l?1}\\ z_l& =FFN(LN(z_l))+z_l\end{array}$$

locally-enhanced positional encoding (LePE)

Comparison among different positional encoding mechanisms: APE and CPE introduce the positional information before feeding into the Transformer blocks, while RPE and our LePE operate in each Transformer block. Different from RPE that adds the positional information into the attention calculation, our LePE operates directly upon V and acts as a parallel module. Here we only draw the self-attention part to represent the Transformer block for simplicity.

APE/CPE add positional information before transformer blocks
RPE add positional information within attention calculation
LePE impose positional information upon linearly projected values
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d}})V+EV$$
if all connections in E considered, a huge computation cost required, supposed the most vital positional information is from neighborhood of input
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d}})V+DWConv(V)$$
where, LePE implemented by depth-wise conv: group conv 3x3, groups=embed_dim

computational complexity

in ViT, given input feature map $x\in R^{h\times w\times C}$, FLOPs of MSA is
$$\Omega (MSA)=4hw{C}^2+2(hw{)}^{2}C$$
for $\frac{1}{2}{n}_{heads}$ horizontal stripes, replace w with sw
$$\Omega (h)=2w(sw)C^2+(w\times sw{)}^{2}C$$
for $\frac{1}{2}{n}_{heads}$ vertical stripes, replace h with sw
$$\Omega (w)=2h(sw)C^2+(h\times sw{)}^{2}C$$
for CS-WMSA, batchsize $\times n_{strips}=\frac{w}{ws}$ or $\frac{h}{ws}$
$$\Omega (CS?WMSA)=\Omega (h)\times \frac{w}{sw}+\Omega (w)\times \frac{h}{sw}=4hw{C}^2+sw(h+w)hwC$$

architecture variants

Detailed configurations of different variants of CSWin Transformer. Note that the FLOPs are calculated with 224x224 input.

Experiment

image classification

dataset ImageNet-1K, with augmentation as DeiT
optimizer AdamW: batchsize=1024, 300 epochs, init lr=1e-3, weigh decay=0.05 or 0.1, linear warm-up 20 epochs, cosine decay
stochastic depth 0.1, 0.3, 0.5 for CSWin-T, CSWin-S, CSWin-B

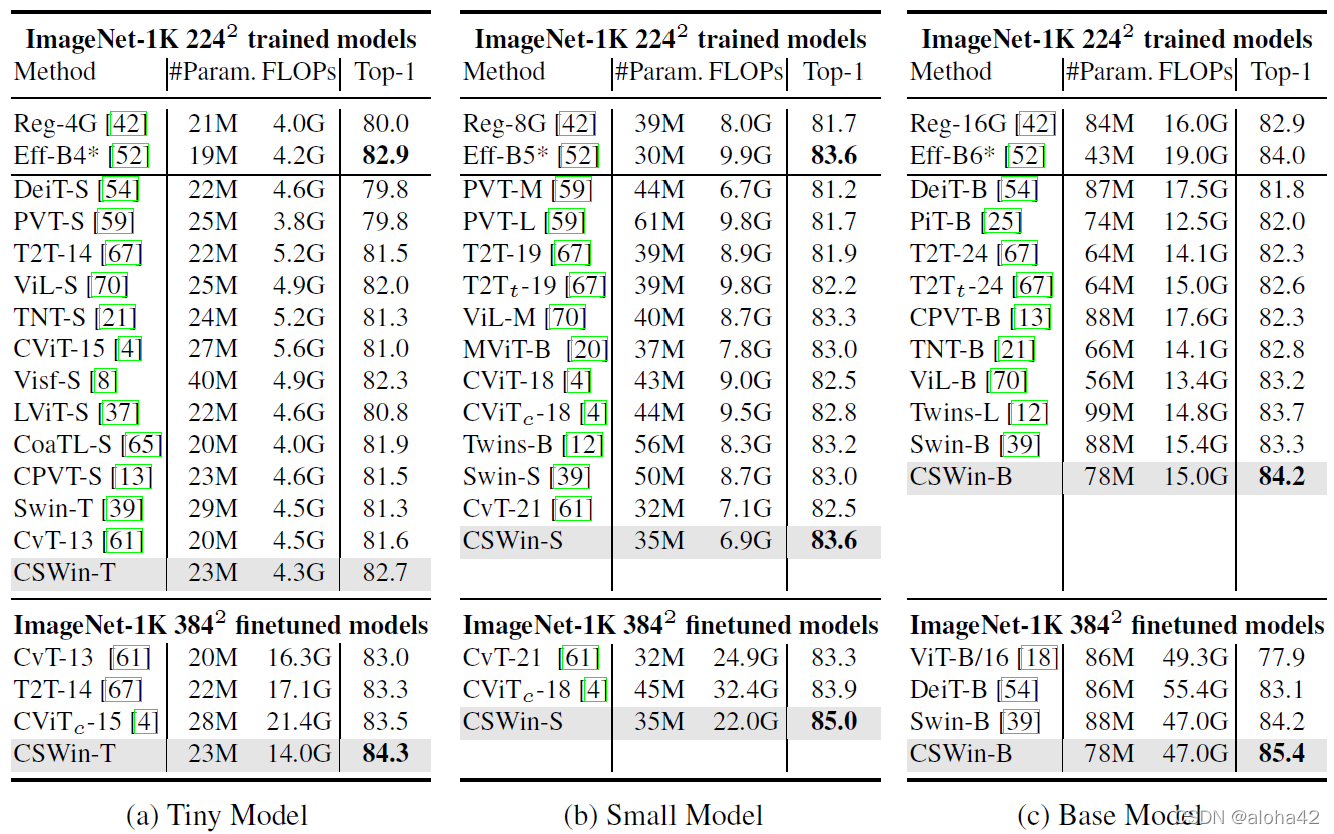
Comparison of different models on ImageNet-1K classification. “*” means the EfficientNet are trained with other input sizes. Here the models are grouped based on the computation complexity.

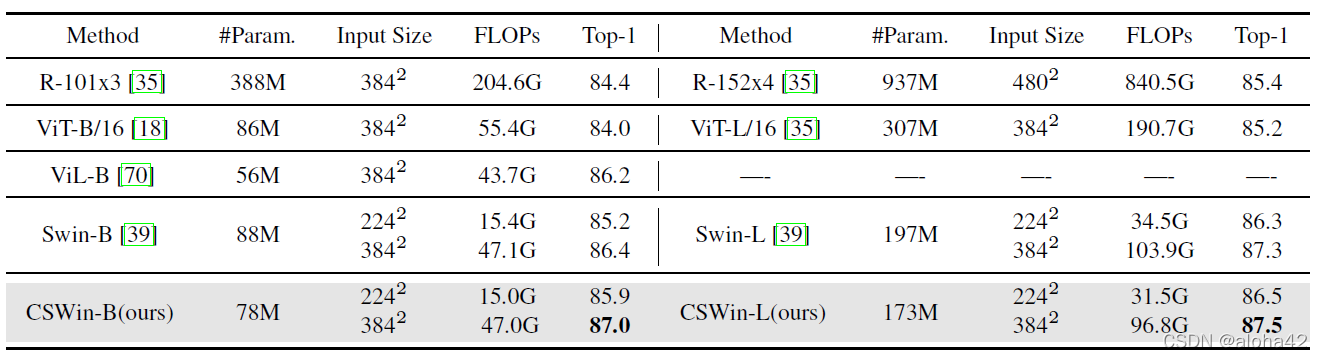
• pre-training
  dataset ImageNet-21K
  optimizer AdamW: batchsize=2048, 90 epochs, init lr=1e-3, weigh decay=0.1 or 0.2
• fine-tuning
  dataset ImageNet-1K
  optimizer AdamW: batchsize=512, 30 epochs, lr=1e-5, weigh decay=1e-8
  stochastic depth 0.1 for both CSWin-B, CSWin-L

ImageNet-1K fine-tuning results by pre-training on ImageNet-21K datasets.

object detection and instance segmentation

framework Mask R-CNN
dataset COCO

• 1x schedule
  optimizer AdamW: batchsize=16, 12 epochs, init lr=1e-4, weigh decay=0.05, decay rate=0.1 at 8, 11-th epoch
• 3x-MS schedule
  optimizer AdamW: batchsize=16, 36 epochs, init lr=1e-4, weigh decay=0.05, decay rate=0.1 at 27, 33-th epoch

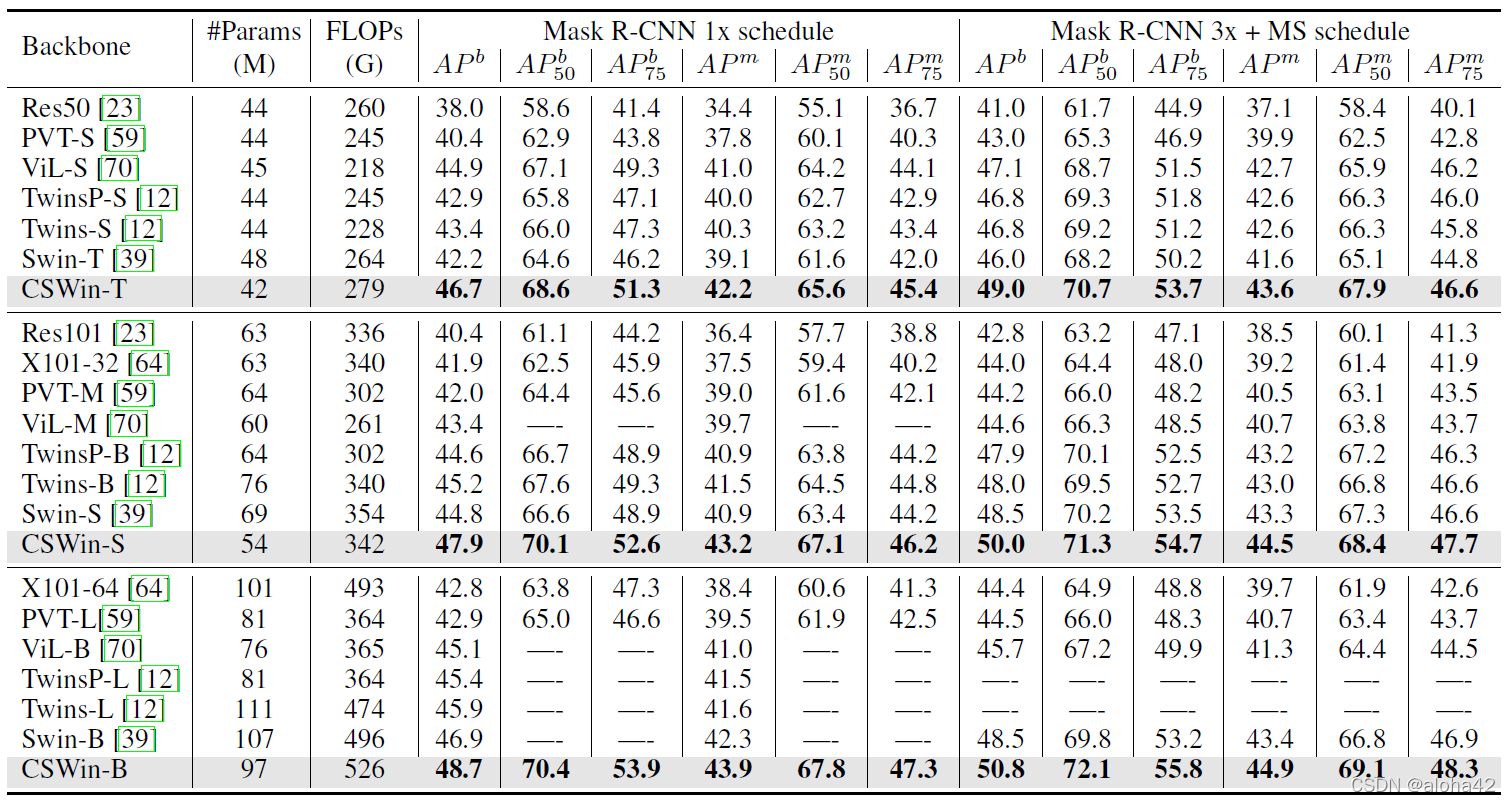
Object detection and instance segmentation performance on the COCO val2017 with the Mask R-CNN framework. The FLOPs (G) are measured at resolution 800x1280, and the models are pre-trained on the ImageNet-1K dataset.

framework Cascade Mask R-CNN
dataset COCO
optimizer AdamW: batchsize=16, 36 epochs, init lr=1e-4, weigh decay=0.05, decay rate=0.1 at 27, 33-th epoch

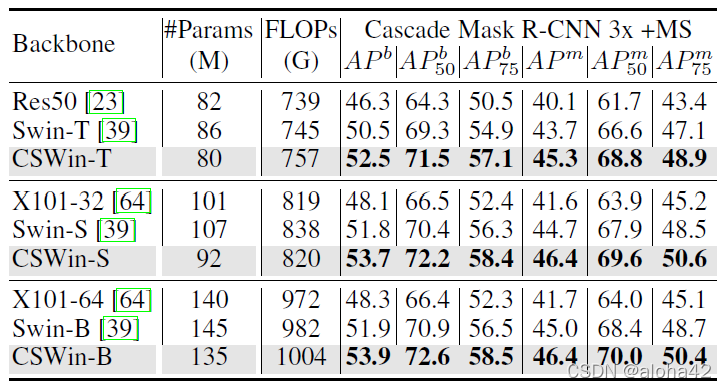
Object detection and instance segmentation performance on the COCO val2017 with Cascade Mask R-CNN.

semantic segmentation

framework Semantic FPN
dataset ADE20K
optimizer AdamW: batchsize=16, 80K iterations, init lr=1e-4, weight decay=1e-4

framework UPerNet
dataset ADE20K
optimizer AdamW: batchsize=16, 160K iterations, init lr=6e-5, weigh decay=5e-4, linear warm-up 1500 iterations, linear decay
stochastic depth 0.1, 0.3, 0.5 for CSWin-T, CSWin-S, CSWin-B

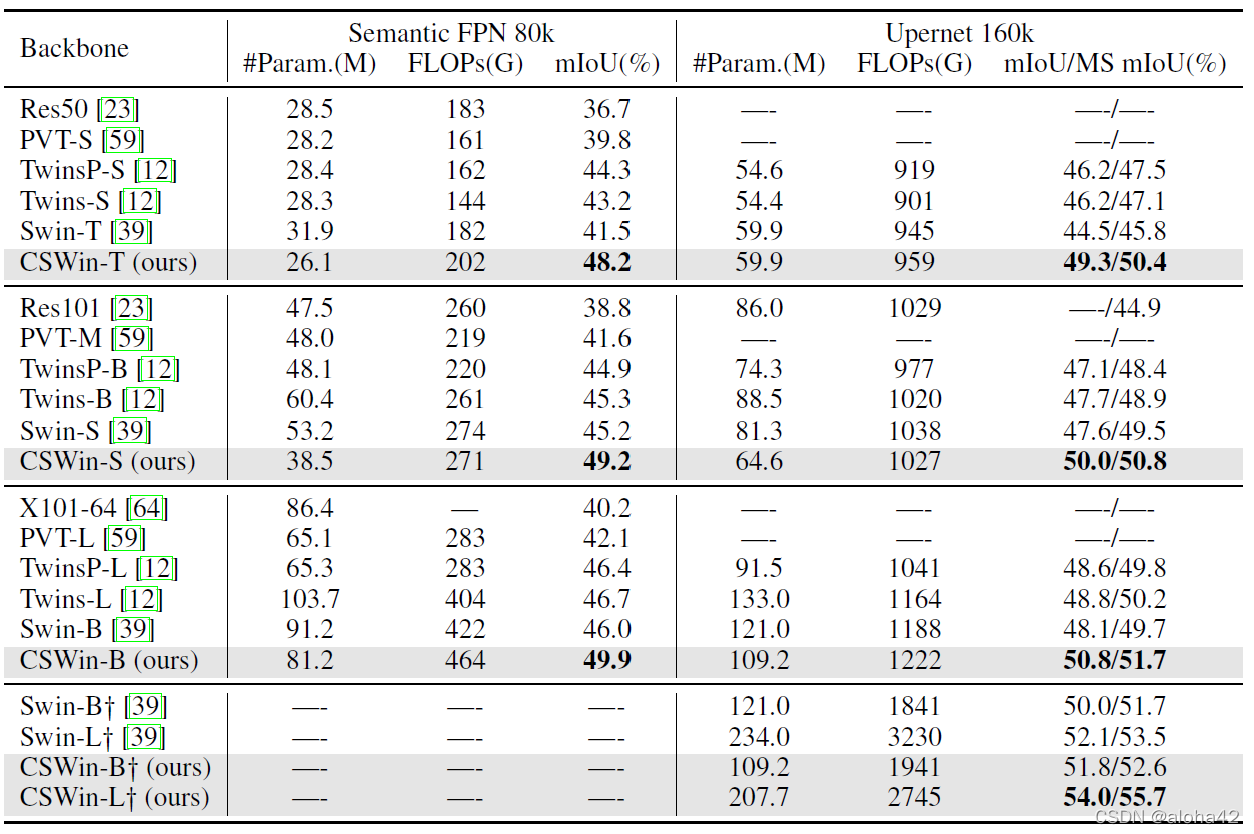
Performance comparison of different backbones on the ADE20K segmentation task. Two different frameworks semantic FPN and Upernet are used. FLOPs are calculated with resolution 512x2048. “+” means the model is pretrained on ImageNet-21K and finetuned with 640x640 resolution.

ablation study

component analysis

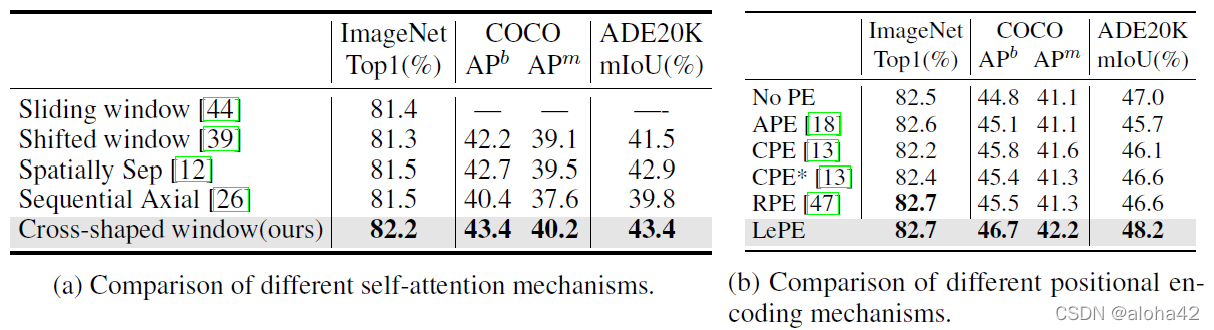
Ablation study of each component to better understand CSWin Transformer. “SA”, “Arch”,“CTE” denote “Self-Attention”, “Architecture”, and “Convolutional Token Embedding” respectively.

1. evaluate baseline that fixes sw=1 for the first three stages and observe dramatic performance drop
   indicate that adjusting sw to enlarge attention area is very crucial
2. change parallel self-attention design into sequential counterpart without multi-heads grouping and find performance drop
   indicate that multi-heads grouping is effective

self-attention mechanism
shallow-wide design used in above subsection: 2, 2, 6, 2 blocks for four stages, base channel is 96
apply non-overlapped token embedding and RPE in above models

Ablation study of different self-attention mechanisms and positional encoding mechanisms. “*” denotes applying CPE before every Transformer block.

positional encoding
positional encoding bring performance gain by introducing local inductive bias
LePE perform better on downstream tasks where input resolution varies

stripes width
vary [$s{w}_1$, $s{w}_2$, $s{w}_3$] of the first three stages of CSWin-T and keep the last stage with $s{w}_4=7$

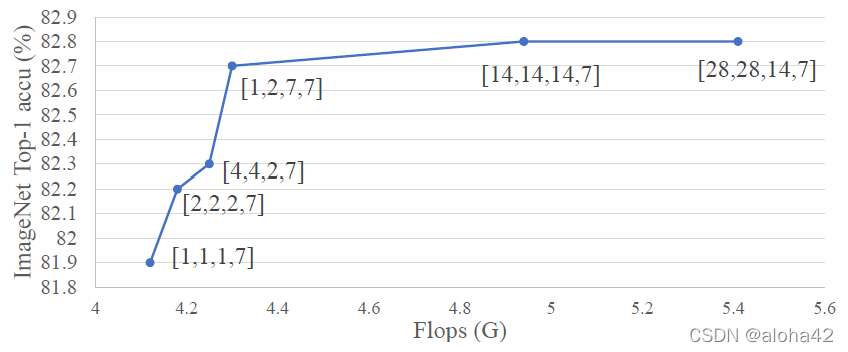
Ablation study on different stripes width. We show the sw of each stage with the form [$s{w}_1$, $s{w}_2$, $s{w}_3$, $s{w}_4$] beside each point and X axis is its corresponding Flops.

with increase of sw, FLOPs increase and accuracy improve greatly at the beginning and slow down when [$s{w}_1$, $s{w}_2$, $s{w}_3$] are large enough
default setting [1, 2, 7, 7] for [$s{w}_1$, $s{w}_2$, $s{w}_3$, $s{w}_4$] achieve a better trade-off for accuracy and computation cost