开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 统一Pearl与Rubin的因果图模型：Single-World Intervention Graphs -> 正文阅读

[人工智能]统一Pearl与Rubin的因果图模型：Single-World Intervention Graphs

本文是Single World Intervention Graphs (SWIGs): Unifying the Counterfactual and Graphical Approaches to Causality论文的笔记

Single World Intervention Graphs

Rubin的potential outcome框架和 Juder peral 的DAG的模型，一直以来都处于割裂状态，这里用一个统一框架来统一两者。

我们知道在Rubin的potential outcome框架下，有很多必要的假设，比如ignorability

$X\bot Y( X=0) |L\ and\ X\bot Y( X=1) |L$

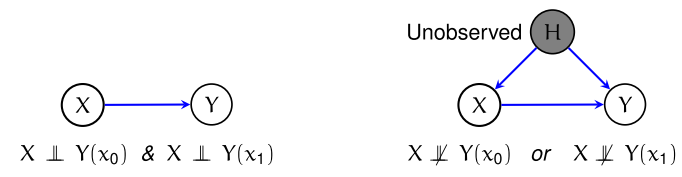
在这里插入图片描述

这个假设可以理解为，不管我的X的选择是什么，都不会对“潜在”的结果有任何影响，更直白点地说就是， $\displaystyle Y( 0) ,Y( 1)$ 是一个世界本来存在的值，X只是选择看哪个而已。然而这样的表述总是很不直观，而且 $\displaystyle Y( 0) ,Y( 1)$ 是没有出现在图上的。有没有可能用一个图结果来刻画这些“潜在”的假设呢？

当满足ignorability假设我们就可以从观测数据中识别出 $\displaystyle Y( 0) ,Y( 1)$ 。然而Pearl也考虑过类似的问题，但他是考虑 $\displaystyle P( Y,do( X))$ 这样的分布是否可识别。从某种程度上来讲，potential outcome这套框架其实能提供更多的信息，因为使用do操作是没有办法对counterfactual建模的，而potential outcome框架却可以。

但是potential outcome这一框架往往不直观 $\displaystyle Y( 0) ,Y( 1)$ 根本没有在图上出现，我们没有办法直观地看到，他跟X到底是否独立。这里介绍一种Single-World Intervention Graphs (SWIGs)，他可以帮我们在图上“画出” $\displaystyle Y( 0) ,Y( 1)$ 这些本来在DAG上不存在的变量，然后用最基本的D-separated就可以一眼看出其所有的独立性!

SWIG的构造方法就是将干预变量X进行node splitting：

在这里插入图片描述

此时，从图上就能看出来， $\displaystyle X\bot Y( 0)$ ，于是有

$P (X = x, Y (0) = y) = P (X = x) P (Y (0) = y)$

其中

$P (Y (0) = y) = P (Y = y ∣ X = 0)$

类似的，X=1也能得到类似的图与结论。你可以发现，这个图每次只能表示一个x的状态(这也是被称为single-world的原因，每次只能观测到一个世界)，我们可以引入模板来作为world的选择，

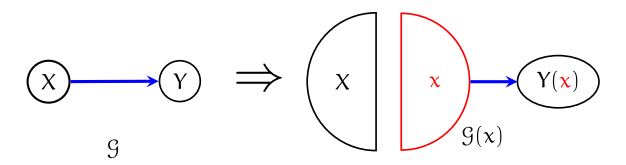
在这里插入图片描述

从而不同的 $\displaystyle \mathcal{G}( x_{0}) ,\mathcal{G}( x_{1})$ 可以用来分别表达不同的 $\displaystyle x$ 的取值。需要注意的是，这个图只是说明了 $\displaystyle X\bot Y( 0)$ 和 $\displaystyle X\bot Y( 1)$ 成立，并没有假设 $\displaystyle X\bot Y( 0) ,Y( 1)$ ，事实上，这样的写法是不对的，我们需要的就只是 $\displaystyle X\bot Y( 0)$ 和 $\displaystyle X\bot Y( 1)$ 。

用SWIG推导back-door formula

现在我们尝试用SWIG来推导出back-door准则，

在这里插入图片描述

从上图可以看到显然， $\displaystyle X\bot Y( x) |L$ 成立，因此

$\begin{aligned} P( Y( x) =y) & =\sum _{l} P( Y( x) =y|L=l) P( L=l)\\ & =\sum _{l} P( Y( x) =y|L=l,X=x) P( L=l)\\ & =\sum _{l} P( Y=y|L=l,X=x) P( L=l) \end{aligned}$

这就推出来了。

这篇文章还提到Rubin这套模型与pearl的SEM模型的优势在于，SEM由于要假设噪声是相互独立的，而这一假设是无法通过随机试验检验的，而Rubin这一套模型是完全可检验的，因此更有优势。

g-formula

g-formula可以看做是一种更加一般化的back-door，它给出了更一般情况下，potential outcome的识别方法，即在干预后的分布中，如何从观测数据中计算出potential outcome。

在这里插入图片描述

举个例子，考虑一个sequence treatments的情况：

在这里插入图片描述

我们有

$\begin{aligned} P( Y( a_{0} ,a_{1}) =y) & =\sum _{l} P( L( a_{0}) =l,Y( a_{0} ,a_{1}) =y)\\ & =\sum _{l} P( L=l\mid A_{0} =a_{0}) P( Y=y\mid A_{0} =a_{0} ,L=l,A_{1} =a_{1}) \end{aligned}$

这里第二个等于号，其实就是相当于考虑上述推论18中，令 $\displaystyle B=\{L,Y\}$

事实上，在有隐变量的时候也仍然适用，比如

在这里插入图片描述

H是隐的，但此时该式子同样适用

$\begin{aligned} P( Y( a_{0} ,a_{1}) =y) & =\sum _{l,h} p( l\mid h,a_{0}) p( y\mid a_{1} ,l,a_{0} ,h) p(h)\\ ( H\bot A_{0}) & =\sum _{l,h} p( l\mid h,a_{0}) p( y\mid a_{1} ,l,a_{0} ,h) p(h|a_{0} )\\ & =\sum _{l,h} p( l,h\mid a_{0}) p( y\mid a_{1} ,l,a_{0} ,h)\\ & =\sum _{l,h} p( h\mid l,a_{0}) p( y\mid a_{1} ,l,a_{0} ,h) p( l|a_{0})\\ ( H\bot A_{1} |A_{0} ,L) & =\sum _{l,h} p( h\mid l,a_{0} ,a_{1}) p( y\mid a_{1} ,l,a_{0} ,h) p( l|a_{0})\\ & =\sum _{l} p( l\mid a_{0})\sum _{h} p( h\mid a_{1} ,l,a_{0}) p( y\mid a_{1} ,l,a_{0} ,h)\\ & =\sum _{l} p( l\mid a_{0})\sum _{h} p( y,h\mid a_{1} ,l,a_{0})\\ & =\sum _{l} p( l\mid a_{0}) p( y\mid a_{1} ,l,a_{0}) \end{aligned}$

甚至一个更复杂的case也是可识别的

在这里插入图片描述

其原因在于，他们都满足了ignorability，即

$a_{0} ,a_{1}) \bot A_{1}( a_{0}) |L( a_{0}) ,A_{0} \ and\ Y( a_{0} ,a_{1}) \bot A_{0}$

也就是response（条件）独立于其干预的变量.

这篇文章的内容还有很多，推荐大家去看看。

参考资料

Richardson, Thomas S., and James M. Robins. “Single world intervention graphs (SWIGs): A unification of the counterfactual and graphical approaches to causality.” Center for the Statistics and the Social Sciences, University of Washington Series. Working Paper 128.30 (2013): 2013.

Single World Intervention Graphs (SWIGs) talk slider

Richardson, Thomas S., and James M. Robins. “Single world intervention graphs: a primer.” Second UAI workshop on causal structure learning, Bellevue, Washington. 2013.

Malinsky, Daniel, Ilya Shpitser, and Thomas Richardson. “A potential outcomes calculus for identifying conditional path-specific effects.” The 22nd International Conference on Artificial Intelligence and Statistics. PMLR, 2019.

Unifying the Counterfactual and Graphical Approaches to Causality

Yao, Liuyi, et al. “A survey on causal inference.” ACM Transactions on Knowledge Discovery from Data (TKDD) 15.5 (2021): 1-46.