本软件是基于TensorFlow深度学习框架,运用LeNet-5卷积神经网络模型和mnist手写数字识别数据集所设计的手写数字识别软件。
具体实现如下:
1.读入数据:运用TensorFlow深度学习框架,下载并读入mnist手写数字识别数据集。
2.构建模型:用神经元构建神经网络,定义神经网络的权重和偏置项来进行前向计算,并使用Softmax Regression模型来进行Softmax分类,即可得到每一类图像特征所对应数字的概率。
3.训练模型:设置训练参数(训练轮次、训练样本量、训练批次、显示力度、学习率等),定义交叉熵损失函数,选择梯度下降优化器来使得损失最小化,用argmax函数找出概率最大的对应数字,并计算准确率。
4.评估模型:用训练集和验证集完整训练后,在测试集上评估模型的准确率。
5.应用模型:模型构建完成后,应用模型,用鼠标写入数字进行识别。
6.用户界面:普通用户可注册账号、输入账号密码登录。管理员用户可以对用户账号进行增、删、改操作。登录后可设置训练参数来训练自己的模型,训练完成后即可应用自己的模型进行手写数字识别。每个账号训练的模型、写入的图像和识别的结果都可保存在自己的账号上(本地的文件里)。
一、研究背景、概况及意义
手写数字识别是利用机器或计算机自动辨认手写体阿拉伯数字的一种技术,是光学字符识别技术的一个分支。该技术可以应用到邮政编码、财务报表、税务系统数据统计、 银行票据等手写数据自动识别录入中。由于不同的人所写的字迹都不相同,对大量的手写体数字实现完全正确地识别不是一件简单的事情。随着全球信息化的飞速发展、数据量的急速增长以及对自动化程度要求的不断提高,手写体数字识别的应用需求急迫。因此,研究一种准确又高效的手写数字识别方法有着非常重大的现实意义和十分广阔的应用前景。
手写数字识别中以往流行的识别方法有三种:隐马尔科夫模型(HMM)、支持向量机(SVM)、人工神经网络(ANN),对复杂分类问题的数学函数表示能力以及网络的泛化能力有限,往往不能达到高识别精度的要求。随着深度学习(deep learning,DL)的不断发展和科学研究的不断深入,卷积神经网络(Convolutional Neural Network,CNN)的出现为解决这个问题提供了可能。它最初由美国学者Yann LeCun等提出,是一种层与层之间局部连接的深度神经网络,最常用于分析视觉图像,受生物自然视觉认知机制(动物视觉皮层细胞负责检测光学信号)启发而来,是一种特殊的多层前馈神经网络。它的人工神经元可以响应一部分覆盖范围内的周围单元,对于大型图像处理有出色表现。一个卷积神经网络通常包括输入输出层和多个隐藏层,隐藏层通常包括卷积层和RELU层(即激活函数)、池化层、全连接层和归一化层等。作为深度学习中最成功的模型之一,卷积神经网络已成为当前图像识别领域的研究热点,使得手写数字识别在识别率和识别速度上,都上了一个新台阶。
作为最早的卷积神经网络模型之一,也是最近大量神经网络架构的起点,LeNet-5通过巧妙的设计,利用卷积、参数共享、池化等操作提取特征,避免了大量的计算成本,最后再使用全连接神经网络进行分类识别。LeNet-5共有7层(不包括输入层),主要由卷积层、下采样层、全连接层以及输出层组成。输入层采用的是3232像素大小的蹄片,卷积层采用的是55大小的卷积核,且卷积核每次滑动一个像素。下采样层将卷积层2828或1010的特征图谱以22为单位的下采样得到1414或55的图。最后全连接层将所有的节点连接起来传给输出层。输出层共有10个节点,分别代表数字0到9。因此用LeNet-5模型搭建手写数字识别模型是非常直观且有重要意义的。
二、研究主要内容
本软件是基于TensorFlow深度学习框架,运用LeNet-5卷积神经网络模型和mnist手写数字识别数据集所设计的手写数字识别软件。LeNet-5共有7层(不包括输入层),主要由卷积层、下采样层、全连接层以及输出层组成。输入层采用的是3232像素大小的蹄片,卷积层采用的是55大小的卷积核,且卷积核每次滑动一个像素。下采样层将卷积层2828或1010的特征图谱以22为单位的下采样得到1414或55的图。最后全连接层将所有的节点连接起来传给输出层。输出层共有10个节点,分别代表数字0到9。具体实现如下:
1.读入数据:
运用TensorFlow深度学习框架,下载并读入mnist手写数字识别数据集。
2.构建模型:
用神经元构建神经网络,定义神经网络的权重和偏置项来进行前向计算,并使用Softmax Regression模型来进行Softmax分类,即可得到每一类图像特征所对应数字的概率。
3.训练模型:
设置训练参数(训练轮次、训练样本量、训练批次、显示力度、学习率等),定义交叉熵损失函数,选择梯度下降优化器来使得损失最小化,用argmax函数找出概率最大的对应数字,并计算准确率。
4.评估模型:
用训练集和验证集完整训练后,在测试集上评估模型的准确率。
5.应用模型:
模型构建完成后,应用模型,用鼠标写入数字进行识别。
6.用户界面:
普通用户可注册账号、输入账号密码登录。管理员用户可以对用户账号进行增、删、改操作。登录后可设置训练参数来训练自己的模型,训练完成后即可应用自己的模型进行手写数字识别。每个账号训练的模型、写入的图像和识别的结果都可保存在自己的账号上(本地的文件里)。
三、研究步骤、方法及措施
1.课题调研:
查阅与课题相关的书籍、文献资料、网络资源等,对课题的发展方向、研究意义和所需要的技术、资源进行全面了解,对课题实现有较为明确的预期和计划。由于本科期间对深度学习、神经网络等方面的知识了解较少,需要查阅并深入学习相关文献知识,从而打下坚实的基础。
2.技术学习:
需要熟悉python与TensorFlow编程,了解深度学习与LeNet-5卷积神经网络,掌握相关算法与函数。Python与TensorFlow也并未学习过,但Python和TensorFlow在机器学习、深度学习或其他计算领域都具有广泛运用,因而借此机会可以掌握新的编程语言和架构。
3.方法设计:
根据相关资料和预期计划,对软件涉及的方法进行完整的设计,确保软件在理论上是可行的。
4.初步编码:
在已有需求分析、功能设计的基础上,运用python、TensorFlow编程等相应技术实现论文中所涉及的方法,测试其在实际中是可行的。数字识别功能初步完成后,对用户界面进行设计和完成。
5.改进和维护:
根据实际编码和方法理论中的差异,以及测试结果的精度和预期的差距,通过改进运用函数或调整测试参数等方式,对软件进行优化。
参考文献:
参考文献
[1] Lécun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11):2278-2324.
[2] LECUN Y, BENGIO Y, HINTON G, et al. Deep Learning[J]. Nature, 2015, 521(7533):436-444.
[3] TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems[J]. 2016.
[4] 杜敏, 赵全友. 基于动态权值集成的手写数字识别方法[J]. 计算机工程与应用, 2010, 046(027):182-184.
[5] 刘炀, 汤传玲, 王静, et al. 一种基于BP神经网络的数字识别新方法[J]. 微型机与应用, 2012.
[6] El-Sawy A , El-Bakry H , Loey M . CNN for Handwritten Arabic Digits Recognition Based on LeNet-5[J]. 2016.
[7] 吕国豪, 罗四维, 黄雅平, et al. 基于卷积神经网络的正则化方法[J]. 计算机研究与发展, 2014, 51(009):1891-1900.
[8] 尹宝才,王文通,王立春.深度学习研究综述[J].北京工业大学学报,2015:54-65.
[9] Fabien Lauer, Ching Y. Suen, Gérard Bloch.A trainable feature extractor for handwritten digit recognition[J].Pattern Recognition,2007:1816-1824.
[10] 赵志宏,杨绍普,马增强.基于卷积神经网络LeNet-5的车牌字符识别研究[J].系统仿真学报,2010(03):94-97.
实现的思路和方法:
(1)项目简介、理论意义与价值
手写数字识别是利用机器或计算机自动辨认手写体阿拉伯数字的一种技术,是光学字符识别技术的一个分支。该技术可以应用到邮政编码、财务报表、税务系统数据统计、银行票据等手写数据自动识别录入中。由于不同的人所写的字迹都不相同,对大量的手写体数字实现完全正确地识别不是一件简单的事情。随着全球信息化的飞速发展、数据量的急速增长以及对自动化程度要求的不断提高,手写体数字识别的应用需求急迫。因此,研究一种准确又高效的手写数字识别方法有着非常重大的现实意义和十分广阔的应用前景。
手写数字识别中以往流行的识别方法有三种:隐马尔科夫模型(HMM)、支持向量机(SVM)、人工神经网络(ANN),对复杂分类问题的数学函数表示能力以及网络的泛化能力有限,往往不能达到高识别精度的要求。随着深度学习(deep learning,DL)的不断发展和科学研究的不断深入,卷积神经网络(Convolutional Neural Network,CNN)的出现为解决这个问题提供了可能。它最初由美国学者Yann LeCun等提出,是一种层与层之间局部连接的深度神经网络,最常用于分析视觉图像,受生物自然视觉认知机制(动物视觉皮层细胞负责检测光学信号)启发而来,是一种特殊的多层前馈神经网络。它的人工神经元可以响应一部分覆盖范围内的周围单元,对于大型图像处理有出色表现。一个卷积神经网络通常包括输入输出层和多个隐藏层,隐藏层通常包括卷积层和RELU层(即激活函数)、池化层、全连接层和归一化层等。作为深度学习中最成功的模型之一,卷积神经网络已成为当前图像识别领域的研究热点,使得手写数字识别在识别率和识别速度上,都上了一个新台阶。
作为最早的卷积神经网络模型之一,也是最近大量神经网络架构的起点,LeNet-5通过巧妙的设计,利用卷积、参数共享、池化等操作提取特征,避免了大量的计算成本,最后再使用全连接神经网络进行分类识别。LeNet-5共有7层(不包括输入层),主要由卷积层、下采样层、全连接层以及输出层组成。输入层采用的是3232像素大小的蹄片,卷积层采用的是55大小的卷积核,且卷积核每次滑动一个像素。下采样层将卷积层2828或1010的特征图谱以22为单位的下采样得到1414或55的图。最后全连接层将所有的节点连接起来传给输出层。输出层共有10个节点,分别代表数字0到9。因此用LeNet-5模型搭建手写数字识别模型是非常直观且有重要意义的。
(2)学生本人工作任务及内容
本软件是基于TensorFlow深度学习框架,运用LeNet-5卷积神经网络模型和mnist手写数字识别数据集所设计的手写数字识别软件。用户可以按照所需精确度的要求,通过设置训练参数对手写数字识别模型进行训练,从而得到符合自身要求的模型,并用鼠标在相应写入区域写入数字进行识别。
基本原理如下:
LeNet-5共有7层(不包括输入层),主要由卷积层、下采样层、全连接层以及输出层组成。输入层采用的是3232像素大小的蹄片,卷积层采用的是55大小的卷积核,且卷积核每次滑动一个像素。下采样层将卷积层2828或1010的特征图谱以22为单位的下采样得到1414或55的图。最后全连接层将所有的节点连接起来传给输出层。输出层共有10个节点,分别代表数字0到9。
具体实现如下:
1、读入数据:
运用TensorFlow深度学习框架,下载并读入mnist手写数字识别数据集。
2、构建模型:
用神经元构建神经网络,定义神经网络的权重和偏置项来进行前向计算,并使用Softmax Regression模型来进行Softmax分类,即可得到每一类图像特征所对应数字的概率。
3、训练模型:
设置训练参数(训练轮次、训练样本量、训练批次、显示力度、学习率等),定义交叉熵损失函数,选择梯度下降优化器来使得损失最小化,用argmax函数找出概率最大的对应数字,并计算准确率。
4、评估模型:
用训练集和验证集完整训练后,在测试集上评估模型的准确率。
5、应用模型:
模型构建完成后,应用模型,用鼠标写入数字进行识别。
6、用户界面:
普通用户可注册账号、输入账号密码登录。管理员用户可以对用户账号进行增、删、改操作。登录后可设置训练参数来训练自己的模型,训练完成后即可应用自己的模型进行手写数字识别。每个账号训练的模型、写入的图像和识别的结果都可保存在自己的账号上(本地的文件里)。
算法原理以及代码解析
图像卷积:
图像卷积能够自动提取图像中的特征,减少多余信息,用于神经网络中,具有替代人工设计特征的功能。图像卷积过程也称特征学习,特征学习能够自动适配新的任务,只需在新数据上进行训练,自动找出新的卷积核,可以避免繁重的特征工程。获取卷积核的函数:
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
定义一个卷积函数:
def conv2d(x,W):
return tf.nn.conv2d(x,W,[1,1,1,1],padding=“SAME”)
池化运算:
池化指对卷积后的图像进行采样,以降低卷积图像的维数,即减少参数。此外,池化还能消除信号的偏移和扭曲,增强网络的鲁棒性。池化的方法一般有两种,一种是平均值池化,另一种是最大值池化。将滤波器尺寸取为2x2,最大值池化运算时,在滤波器覆盖的每个区域中提取该区域内像素的最大值,进而得到主要特征。定义一个模板为2x2大小的池化函数:
def max_pool_2x2(x):
return tf.nn.max_pool(x,ksize=[1,2,2,1],
strides=[1,2,2,1],padding=“VALID”)
通过两次2x2池化后,长宽尺寸降低为2x2。把1024维向量转换成10维,对应10个类型后,即可计算交叉熵。
损失函数:
为了训练我们的模型,我们首先需要定义一个指标来评估这个模型是好的。其实,在机器学习,我们通常定义指标来表示一个模型是坏的,这个指标称为成本(cost)或损失(loss),然后尽量最小化这个指标。但是这两种方式是相同的。
一个非常常见的成本函数是“交叉熵”(cross-entropy)。交叉熵产生于信息论里面的信息压缩编码技术,但是它后来演变成为从博弈论到机器学习等其他领域里的重要技术手段。它的定义如下:
(2-1)
y是我们预测的概率分布, y’是实际的分布。比较粗糙的理解是,交叉熵是用来衡量我们的预测用于描述真相的低效性。我们可以首先定义 y’,它的表达式是:y_ = tf.placeholder(tf.float32, [None, 10])
接下来我们需要计算它们的交叉熵,代码如下:
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
首先用 reduce_sum() 方法针对每一个维度进行求和,reduction_indices 是指定沿哪些维度进行求和。然后调用 reduce_mean() 则求平均值,将一个向量中的所有元素求算平均值。这样我们最后只需要优化这个交叉熵就好了。所以这样我们再定义一个优化方法:
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
这里使用了 GradientDescentOptimizer,在这里,我们要求 TensorFlow 用梯度下降算法(gradient descent algorithm)以 0.5 的学习速率最小化交叉熵。梯度下降算法(gradient descent algorithm)是一个简单的学习过程,TensorFlow只需将每个变量一点点地往使成本不断降低的方向移动即可。
Softmax回归:
MNIST的每一张图片都表示一个数字,从0到9。我们希望得到给定图片代表每个数字的概率。比如说,我们的模型可能推测一张包含9的图片代表数字9的概率是80%但是判断它是8的概率是5%(因为8和9都有上半部分的小圆),然后给予它代表其他数字的概率更小的值。
这是一个使用Softmax回归(softmax regression)模型的经典案例。Softmax模型可以用来给不同的对象分配概率。即使在之后,我们训练更加精细的模型时,最后一步也需要用Softmax来分配概率。
Softmax可以看成是一个激励(activation)函数或者链接(link)函数,把我们定义的线性函数的输出转换成我们想要的格式,也就是关于10个数字类的概率分布。因此,给定一张图片,它对于每一个数字的吻合度可以被Softmax函数转换成为一个概率值。Softmax函数可以定义为:
(2-2)
展开等式右边的子式,可以得到:
(2-3)
对于Softmax回归模型可以用下面的图解释,对于输入的xs加权求和,再分别加上一个偏置量,最后再输入到softmax函数中,把它写成一个等式,我们可以得到:
(2-4)
(2-5)
(2-6)
我们也可以用向量表示这个计算过程:用矩阵乘法和向量相加。这有助于提高计算效率:
(2-7)
可以写成更加紧凑的方式:
(2-8)
可以使用 tf.nn.softmax_cross_entropy_with_logits 直接计算交叉熵:cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=lable,lo gits=y_conv))
运行模型:
定义好了以上内容之后,相当于我们已经构建好了一个计算图,即设置好了模型,我们把它放到 Session 里面运行即可,在运行计算之前,我们需要添加一个操作来初始化我们创建的变量:
init = tf.initialize_all_variables()
在一个Session里面启动我们的模型,并且初始化变量:
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
然后开始训练模型,填入训练参数,训练set步:
for i in range(set): batch_xs, batch_ys = mnist.train.next_batch(50) sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
该循环的每个步骤中,我们都会随机抓取训练数据中的50个批处理数据点,然后我们用这些数据点作为参数替换之前的占位符来运行train_step。
测试模型:
tf.argmax() 是一个非常有用的函数,它能给出某个 tensor 对象在某一维上的其数据最大值所在的索引值。由于标签向量是由 0,1 组成,因此最大值 1 所在的索引位置就是类别标签,比如 tf.argmax(y,1) 返回的是模型对于任一输入x预测到的标签值,而 tf.argmax(y_,1) 代表正确的标签,我们可以用 tf.equal() 方法来检测我们的预测是否真实标签匹配(索引位置一样表示匹配)。
correct_prediction = tf.equal(tf.argmax(y_conv,1),tf.argmax(lable,1))
这行代码会给我们一组布尔值。为了确定正确预测项的比例,我们可以把布尔值转换成浮点数,然后取平均值。例如,[True, False, True, True] 会变成 [1,0,1,1] ,取平均值后得到 0.75。计算精确率为:
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
架构设计:
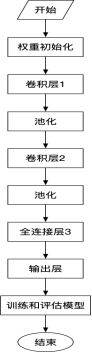
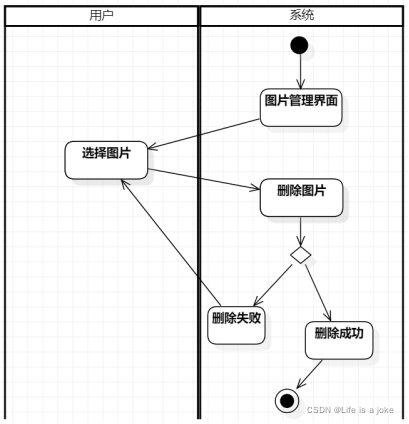
图2-1 流程图
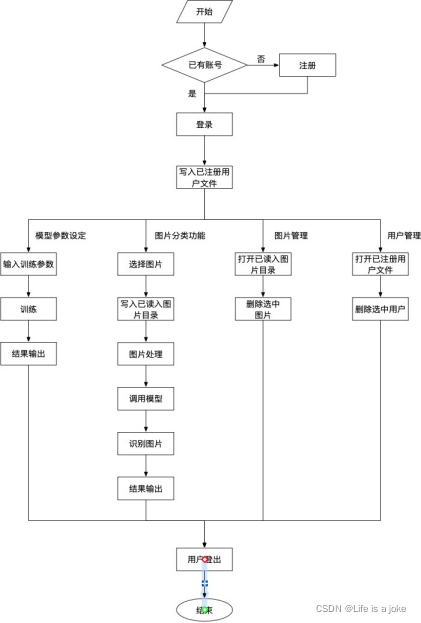
图2-2 功能图
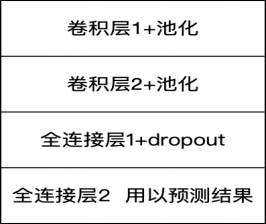
图2-3 网络结构图
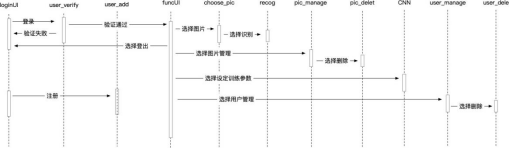
图2-4 循环图
关键代码:
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#权重初始化
#定义一个获取卷积核的函数
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
#定义一个获取偏置值的函数
def bias_variable(shape):
initial = tf.constant(0.1,shape=shape)
return tf.Variable(initial)
#定义一个卷积函数
def conv2d(x,W):
return tf.nn.conv2d(x,W,[1,1,1,1],padding="SAME")
#定义一个池化函数#模板为 2x2 大小
def max_pool_2x2(x):
return tf.nn.max_pool(x,ksize=[1,2,2,1], strides=[1,2,2,1],padding="VALID")
if name == " main ":
mnist = input_data.read_data_sets("data/",one_hot=True) x = tf.placeholder(shape=[None,28*28],dtype=tf.float32) lable = tf.placeholder(shape=[None,10],dtype=tf.float32)
x_image = tf.reshape(x,[-1,28,28,1])
#第一个卷积层
#在每个 5x5 的 patch 中算出 32 个特征W_conv1 = weight_variable([5,5,1,32]) b_conv1 = bias_variable([32])
#卷积核与输入的 x_image 进行卷积,再最大池化
h_conv1 = tf.nn.relu(conv2d(x_image,W_conv1)+b_conv1) h_pool1 = max_pool_2x2(h_conv1)
#14*14*32
#第二个卷积层
#每个 5x5 的 patch 得到 64 个特征。卷积核大小 5x5x32,共 64 个
W_conv2 = weight_variable([5,5,32,64]) b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2) h_pool2 = max_pool_2x2(h_conv2)
#7*7*64
#全连接层,输出为 1024 维向量
#经过两次 2x2 池化后,长宽尺寸降低为 7x7 W_fc1 = weight_variable([7*7*64,1024]) b_fc1 = weight_variable([1024])
h_pool2_flat = tf.reshape(h_pool2,[-1,7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1)+b_fc1) keep_prob = tf.placeholder(tf.float32)
h_fc1_dropout = tf.nn.dropout(h_fc1,keep_prob=keep_prob)
#把 1024 维向量转换成 10 维,对应 10 个类别
W_fc2 = weight_variable([1024,10])
b_fc2 = weight_variable([10])
y_conv = tf.matmul(h_fc1,W_fc2)+b_fc2
#使用 tf.nn.softmax_cross_entropy_with_logits 直接计算交叉熵
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=lable,lo gits=y_conv))
#定义 train_step
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
#定义测试的准确率
correct_prediction = tf.equal(tf.argmax(y_conv,1),tf.argmax(lable,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
# 创建 Session 和变量初始化
sess = tf.InteractiveSession() sess.run(tf.global_variables_initializer())
#训练 xx 步(训练参数)
for i in range(set):
batch = mnist.train.next_batch(50)
if i % 100==0:
train_accuracy = sess.run(accuracy,feed_dict={ x:batch[0],lable:batch[1],keep_prob: 1.0})
print("step %d, training accuracy %g" % (i, train_accuracy))
_ = sess.run(train_step, feed_dict={x: batch[0], lable: batch[1], keep_prob: 0.5})
print("test accuracy %g" % sess.run(accuracy, feed_dict={
x: mnist.test.images, lable: mnist.test.labels, keep_prob:
1.0}))
saver = tf.train.Saver()
saver.save(sess,'/Users/lige/Desktop/py/model.ckpt')
数据集阐述:
项目使用的是Mnist测试数据集。Mnist是一个入门级的计算机视觉数据集,它包含各种手写数字图片,以及每一张图片对应的标签,相对应的标签是介于0到9的数字,用来描述给定图片里表示的数字。数据集中包含了60000行的训练数据集(mnist.train)、5000 行验证集(mnist.validation)和10000行的测试数据集(mnist.test)。每张图片是 28 x 28 像素,即 784 个像素点,我们可以把它展开形成一个向量,即长度为 784 的向量。如下,这四张图片的标签分别是5,0,4,1。
图1 数字图片示例
可以通过MNIST数据集的官网进行下载:http://yann.lecun.com/exdb/mnist/下载下来的数据集中包含了60000行的训练数据集(mnist.train)、5000 行验证集(mnist.validation)和10000行的测试数据集(mnist.test)。这样的切分很重要,在机器学习模型设计时必须有一个单独的测试数据集不用于训练而是用来评估这个模型的性能,从而更加容易把设计的模型推广到其他数据集上(泛化)。
正如前面提到的一样,每一个 MNIST 数据单元有两部分组成:一张包含手写数字的图片和一个对应的标签。我们把这些图片设为 xs,把这些标签设为 ys。训练数据集和测试数据集都包含 xs 和 ys,比如训练数据集的图片是 mnist.train.images ,训练数据集的标签是 mnist.train.labels,每张图片是 28 x 28 像素,即 784 个像素点,我们可以把它展开形成一个向量,即长度为 784 的向量。
每一张图片包含28X28个像素点。可以用一个数字数组来表示这张图片:
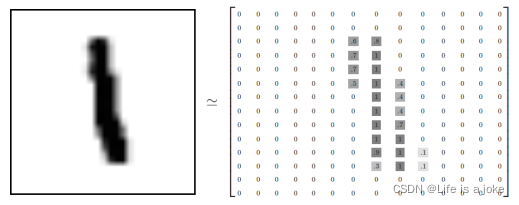
图2 数字数组表示
把这个数组展开成一个向量,长度是 28x28 = 784。如何展开这个数组(数字间的顺序)不重要,只要保持各个图片采用相同的方式展开。从这个角度来看,MNIST数据集的图片就是在784维向量空间里面的点, 并且拥有比较复杂的结构 (提醒: 此类数据的可视化是计算密集型的)。
展平图片的数字数组会丢失图片的二维结构信息。这显然是不理想的,最优秀的计算机视觉方法会挖掘并利用这些结构信息,我们会在后续教程中介绍。但是在这个教程中我们忽略这些结构,所介绍的简单数学模型,softmax回归(softmax regression),不会利用这些结构信息。
因此,在MNIST训练数据集中,mnist.train.images 是一个形状为[60000, 784]的向量,第一个维度数字就是训练集中包含的图片个数,用来索引图片,第二个维度的数字用来索引每张图片中的像素点。在此张量里的每一个元素,都表示某张图片里的某个像素的强度值,值介于0和1之间。
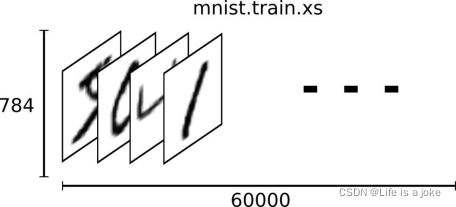
图3 向量表示
相对应的MNIST数据集的标签是介于0到9的数字,用来描述给定图片里表示的数字。为了用于这个教程,我们使标签数据是"one-hot vectors"。一个one-hot向量除了某一位的数字是1以外其余各维度数字都是0。所以在此教程中,数字n将表示成一个只有在第n维度(从0开始)数字为1的10维向量。比如,标签0将表示成([1,0,0,0,0,0,0,0,0,0,0])。因此,mnist.train.labels是一个 [60000, 10]的数字矩阵。
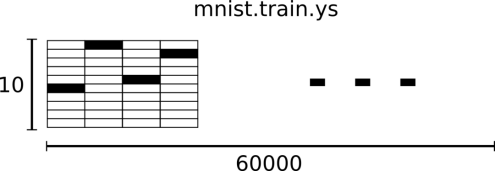
图4 数字矩阵
功能设计
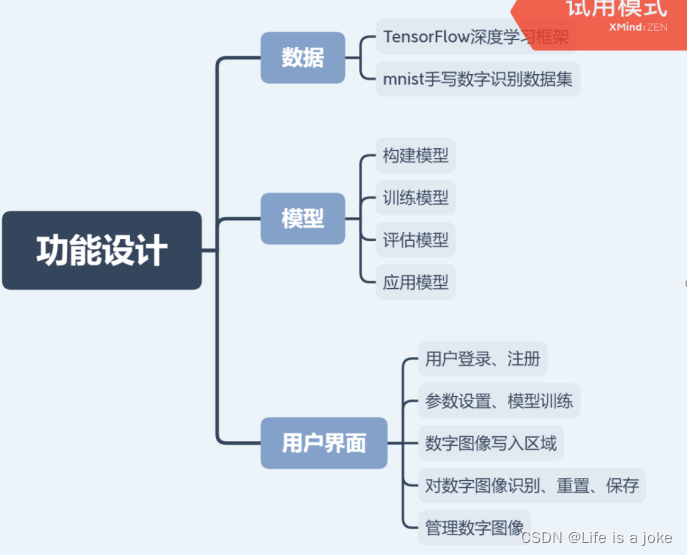
用户使用
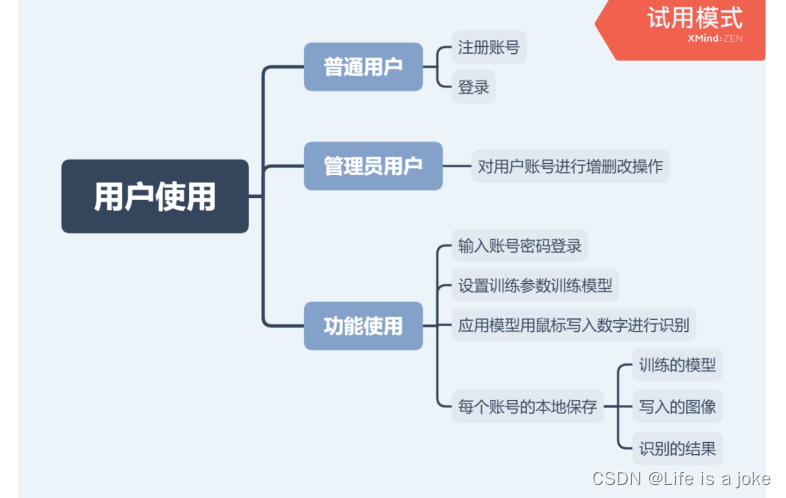
注册账号
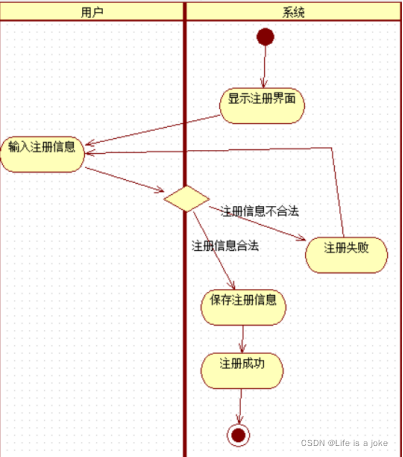

模型训练与测试

数字识别
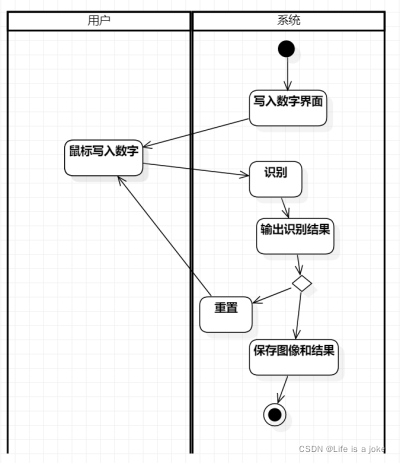
图片管理