[人工智能]【正弦余弦算法】基于精英混沌搜索策略的交替正余弦算法求解单目标优化问题Matlab代码

1 简介

正余弦算法是一种新的基于种群的随机寻优方法,利用正余弦函数使解震荡性地趋于全局最优解,其线性调整策略及较弱的局部搜索能力严重地影响了算法的性能.为了提高正弦余弦算法的计算精度,提出基于精英混沌搜索策略的交替正余弦算法.新算法采用基于对数曲线的非线性调整策略修改控制参数,利用精英个体的混沌搜索策略增强算法的开发能力,并将基于该策略的正余弦算法与反向学习算法交替执行增强算法的探索能力,降低算法的时间复杂度,提高算法的收敛速度.对23个基准测试函数进行仿真实验,与改进的正余弦算法以及最新的基于启发式的算法进行比较,深入的参数实验分析以及比较结果验证了所提出算法的有效性,统计分析证实了所提出算法的优越性.

2 部分代码

function [fitnessgbest, gbest, Curve] = ISCA(X, N, maxgen, lb, ub, dim, fobj)?%% ISCA参数wmax = 0.8; wmin = 0.1;%% 反向学习初始化OX = ub+lb-X;Y = [X; OX];for i = 1:2*N    fitness(i) = fobj(Y(i, :));end% 初始最优[~, sortindex] = sort(fitness);X = Y(sortindex(1:N), :);fitness = fitness(sortindex(1:N));gbest = X(1, :);                        % 群体最优极值fitnessgbest = fitness(1);         % 种群最优适应度值?%% 迭代寻优for t = 1:maxgen    % Eq. (3.4)    a = 2;    r1 = a-t*(a/maxgen);    % r1从a线性递减到0    %% 修改个体位置更新方程    w = wmax-(wmax-wmin)*t/maxgen;    for i = 1:N        for j = 1:dim             % 由Eq. (3.3)更新r2,r3,r4            r2 = (2*pi)*rand();            r3 = 2*rand;            r4 = rand();                        % Eq. (3.3)            if r4 < 0.5                % Eq. (3.1)                X(i, j) =  w*X(i, j)+(r1*sin(r2)*abs(r3*gbest(j)-X(i, j)));            else                % Eq. (3.2)                X(i, j) = w*X(i, j)+(r1*cos(r2)*abs(r3*gbest(j)-X(i, j)));            end        end    end        for i = 1:N        % 边界处理        Flag4ub = X(i, :) > ub;        Flag4lb = X(i, :) < lb;        X(i, :) = (X(i, :).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;        % 更新适应度值        fitness(i) = fobj(X(i, :));                % 更新最优解        if fitness(i) < fitnessgbest            gbest = X(i, :);            fitnessgbest = fitness(i);        end    end       % 记录每代最优解    Curve(t) = fitnessgbest;    % 显示迭代信息%     display(['ISCA:At iteration ', num2str(t), ' the best fitness is ', num2str(Curve(t))]);end??

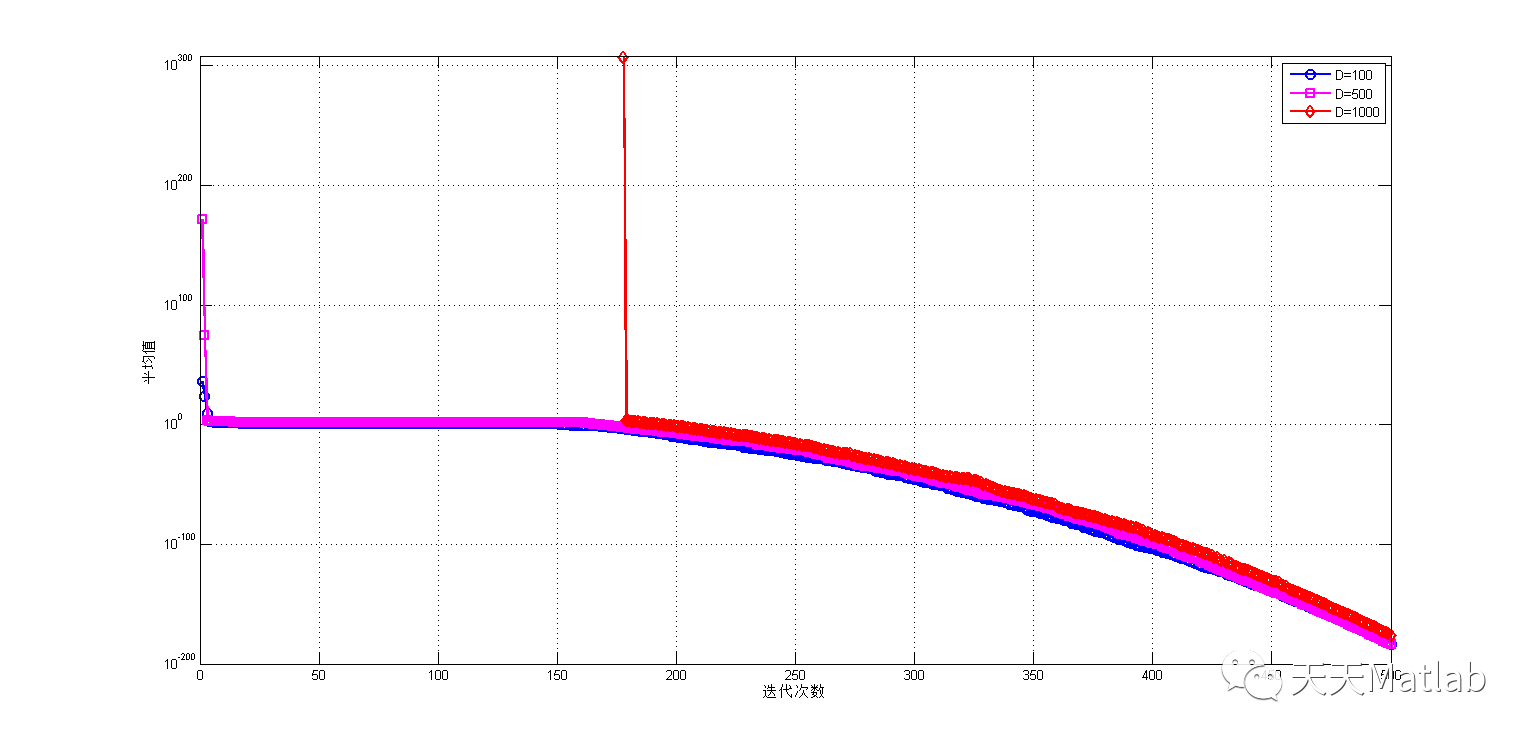
3 仿真结果

4 参考文献

[1]郭文艳, 王远, 戴芳,等. 基于精英混沌搜索策略的交替正余弦算法[J]. 控制与决策, 2019, 34(8):9.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。