序言:
共线性的含义是两个特征(连续型数值特征)之间存在高度相关关系,而多重共线性是一个特征和其他多个特征存在相关关系。这里的相关性一般指线性相关。线性相关指两个变量A,B之间可以存在某个齐次线性方程,例如B=2*A+1,像风控特征中的“近90天拒绝次数”和“近90天申请次数”就存在非常强的线性关系,我们绘制下散点图也能看出来两者之间的线性关系(如下图):
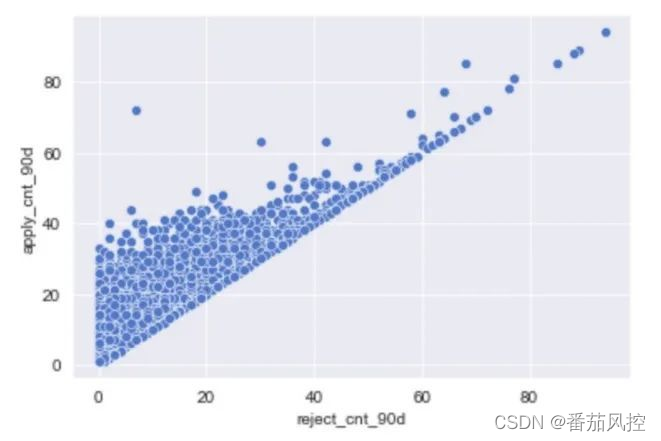
衡量两两相关性一般用皮尔逊相关系数(Pearson correlation),皮尔逊系数的值在-1到1之间,当系数为0时,两者无相关关系,当系数大于0时,两个特征为正相关,小于0时为负相关,系数的绝对值越大,相关性越强,通常情况下通过以下取值范围判断相关程度:
0-0.2:极弱相关或无相关
0.2-0.4:弱相关
0.4-0.6:中等程度相关
0.6-0.8:强相关
0.8-1.0:极强相关
皮尔逊相关系数的计算过程为两个特征(X,Y)之间协方差和标准差的商:
?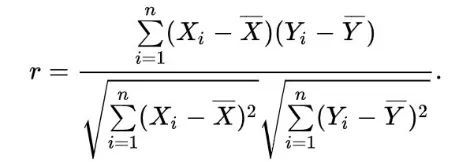
衡量多重共线性一般用方差膨胀系数(VIF),VIF的计算公式为:
?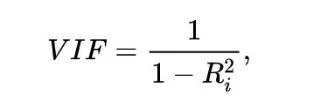
其中Ri为特征X对其余特征做回归分析的负相关系数,VIF的值越大,说明特征之间存在多重共线性的可能性越大,一般来说,VIF超过5或10,说明存在严重的多重共线性。
共线性是风控建模中常见的一种问题,也是值得去深挖研究的问题,本篇文章将基于风控建模最常用的LR,集成模型两种算法出发,探讨共线性对于模型的影响和对共线性特征的处理。
Part1.共线性对于LR的影响
对于模型结果我们主要关注三个方面,一是模型的精度偏差(AUC,KS),二是模型的稳定性/鲁棒性,三是模型的可解释性,共线性对于模型的影响将从这三方面来阐述。
1.对LR精度偏差上的影响
我们先看一下LR的梯度W的更新公式:
W = W - alphadata_matrix.transpose()error
其中alpha是学习率,data_matrix.transpose()为原始数据矩阵,error为真实值和预测值的偏差,可以看到只要模型最后能够收敛,共线性对于LR损失函数的最优化没影响,所以对于精度没什么影响。但这个结果的前提是原始数据不存在什么噪声,我们都知道LR对于噪声比较敏感,实际情况中会一些特征存在噪声,假如有A,B,C三个相关性高的特征,三个特征受到噪声干扰的概率都为10%,如果只挑选其中一个入模,则模型受噪声干扰的概率为10%,如果三个都入模,则受到噪声的概率可以假设为1-0.90.90.9=27.1%,所以入模比较多的共线性特征会增加模型受到噪声干扰的概率,从而影响模型的精度,但从实验结果看,这种影响程度是比较低的,能在接受范围内。
2.对LR稳定性/鲁棒性的影响
共线性特征太多会增加噪声干扰,也会增加特征维度,结果表现为训练集和验证集的效果有明显差距,过拟合风险增加,或者在OOT的时间跨度上精度不稳定。所以对模型的稳定性,健壮性有一定的影响。
3.对LR解释性的影响
1)共线性会使特征的系数符号出现与实际相反的情况,例如某个特征的系数实际为正数,算出来为负数,举个例子:
假设原始的线性回归公式为:
y = w1x1+w2x2+w3x3,w1-w3为系数,x1-x3为特征
模型训练完后得出系数:
y = 3x1+5x2+8x3
这时候加入一个新特征x4,x3与x4高度线性相关,x4=2x3
那回归公式变为:
y = w1x1+w2x2+w3x3+w4x4–>y = w1x1+w2x2+(w3+2w4)x3
此时w3+2w4可以合并成一个新的系数w5,
因为相关性对精度没啥影响,则y = w1x1+w2x2+w3x3 和 y = w1x1+w2x2+w5x3是等价的,之前得出的y = 3x1+5x2+8x3是最优模型,但是引入了x4,w4和w3的权重是分开计算出来的,这样w5=10=w3+2w4,如果方程的解为w3=-2,w4=6,x3的系数符号就变成负数了,这样就会影响x3的可解释性,另外由于w3和w4有无数多的解,使特征系数值的方差增大,模型每次训练得到的系数差异比较大,更加影响模型的解释性。
2)共线性对系数值的影响还会导致本应该显著的特征不显著,本应该不显著的特征呈现显著性,无法从P值的大小来判断显著性,对LR的训练过程和变量筛选造成很大影响。
Part2.LR建模时对共线性的处理
可以发现共线性对LR的最大影响是解释性,由于风控建模中的LR模型非常注重可解释性,所以必须要做特征筛选,去除共线性高的特征。
1.共线性筛选的角度和注意点
1)筛选的特征类型为连续型的数值特征
2)可根据皮尔逊相关系数和方差膨胀系数(vif)来判断是否存在高相关性
皮尔逊相关系数的取值在0-1之间,一般认为0.65或者0.7以上为高度相关,vif>5或>10认为存在高度的多重共线性,两个系数可以选择其一,或者结合使用来做筛选,筛选的最终要求是特征系数值的符号一致。
3)由于风控场景的LR建模会做woe转换,所以要先把特征原始值映射成woe后,再计算相关系数或VIF
2.特征筛选的方法
假设A和B两个特征存在共线性,那要剔除哪个呢?一般来说要基于特征的区分能力,也就是IV值大小,若A的IV比B大,则保留A,删除B。另外如果特征很多,特征之间的关系比较复杂,那怎么筛选比较简单高效呢?这就是下面要介绍的三种方法:前向选择,后向选择,双向选择
1)前向选择:将特征按IV值从大到小进行排序,先计算排名前两个的相关系数,若为高相关,则剔除IV值较小的那一个,然后逐步加入特征,每加入一个,就要判断新加入的和其他特征是否存在高度相关,直到所有特征都加完为止。
2)后向选择:先计算全部特征的相关系数,将高相关的特征挑出来并按IV值从小到大进行排序,先剔除IV最小的那一个,然后再计算一遍相关性,依此进行剔除,每剔除一个就判断剩下特征是否存在共线性,如果不存在,则循环停止。
3)双向选择:在LR中也叫做逐步回归,实现过程就是先做前向选择,每次做完一轮前向选择后马上做后向选择,一直到结束。或者先做后向选择,然后做前向选择,在被剔除的特征中选择最好的加回来看效果,这种方法虽然兼顾了前向和后向的优点,但比较耗费时间。
Part3.共线性对于集成算法的影响
1.对集成算法精度偏差上的影响
风控中集成算法主要用的是随机森林,xgboost,lightgbm,catboost这几种,都是以决策树为基模型,决策树对共线性是不敏感的,这是由于在构建树的过程中,采用贪婪算法做特征选择,只有新特征的信息增益比较大才会加入到模型中,所以共线性高的特征中可能只有一个会被选择,集成算法中每一棵树的构建都是贪婪的,就算特征之间共线性很高也只选择部分特征进入到模型中,所以对精度没有影响,这个结论是针对共线性特征较少的情况。如果共线性特征过多,尤其是那种暴力衍生的方式生成很多相关性高的特征,导致模型训练中重复采样相关性高的特征,这样集成模型追求每个基模型的“好而不同”就会减弱,基模型之间的多样性降低,进而影响模型的效果。
2.对集成算法稳定性/鲁棒性的影响
共线性特征比较多就会引入更多的噪声,对于比较巨大的数据集,大量的样本能很好稀释掉特征空间引入新特征发生的变化,并且决策树对噪声也不敏感。但对于小数据集,这些噪声就会对模型的稳定性和鲁棒性有影响,例如相关特征的噪声数据可能恰好适合某些特定组合的分割选择,但噪声产生的分支对于未来数据预测有很大的偏差。
3.对集成算法可解释性的影响
集成模型可以通过特征重要性来解释特征对模型效果的贡献程度,在xgboost和lightgbm中,计算特征重要性有3种方式:
1)importance_type=weight(默认值),使用特征在所有树中作为分裂属性的次数。
2)importance_type=gain,使用特征在作为划分属性时loss平均的降低量。
3)importance_type=cover,使用特征在作为划分属性时对样本的覆盖度
一般我们用第一种方式来计算重要性,重要性等于10说明特征在所有树中作为分裂属性用到了10次,次数越多,说明特征分裂时带来的信息增益越大,特征区分能力越强。
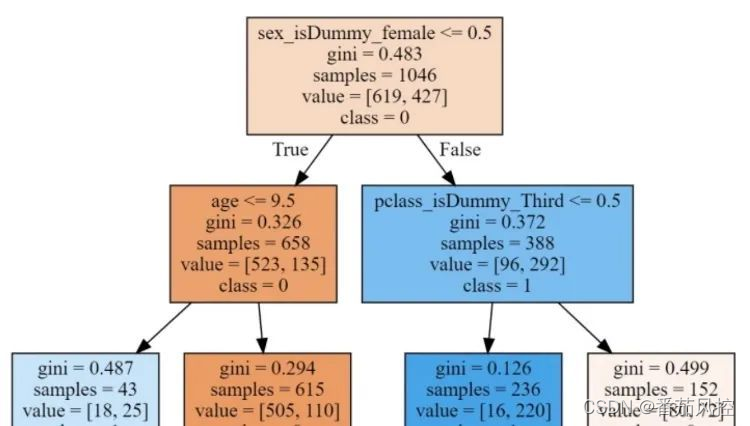
共线性对特征重要性的计算会有影响,举个例子,一个xgb模型有20棵决策树组成,单棵决策树的分裂过程如下图,假如A是个强特征,在每棵树的第一层分裂时都用到了,那A的重要性为1*20 =20,现在加入与它高相关性的特征B,在第一层分裂时,由于A和B高度相关,模型只能选择其中一个来分裂,如果模型随机挑一个,那20棵树里有10棵选择了A,另外10棵选择了B,这样A的重要性就从20变成了10,重要性被稀释掉了,所以共线性会导致计算出的重要性不是真实的,从而影响模型的可解释性。
?
Part4.集成算法建模时对共线性的处理
1)不做处理。相比于LR,共线性对于集成模型的影响相对要小,并且集成模型对于解释性要求不高。如果共线性特征不是很多,且样本量比较大,可以不做处理。笔者在实际应用中也发现共线性筛选如果筛的太多,模型精度会明显下降,这时候就得优先考虑精度影响了。
2)根据IV值做筛选,由于共线性会影响特征重要性的值,所以要选择IV作为评估指标,筛选方法也是用前向/后向/逐步选择,这种情况适用于特征维度很多或者样本量比较少,做共线性筛选一方面通过降维来减小模型复杂度,也可以降低噪声的影响。
以上就是笔者对于共线性问题的探讨,对于共线性特征的处理要根据使用的算法,样本量,特征维度,时间成本来综合考虑,下面总结下共线性筛选的好处:
1)可以显著提高模型训练的速度,共线性特征很多的话,就算损失函数收敛了,但可能参数没有收敛,这样会拉低训练速度。
2)可以提高模型的可解释性,尤其对于LR模型非常重要。
3)减弱噪声对模型的影响,提高模型的稳定性和鲁棒性。
4)通过降维来降低发生过拟合的风险,以及其他未知的风险因素。
Part5.实操—利用python做共线性的可视化和筛选
1.导入样本,样本有5000条数据,30个特征(var_1–var_30)。
?
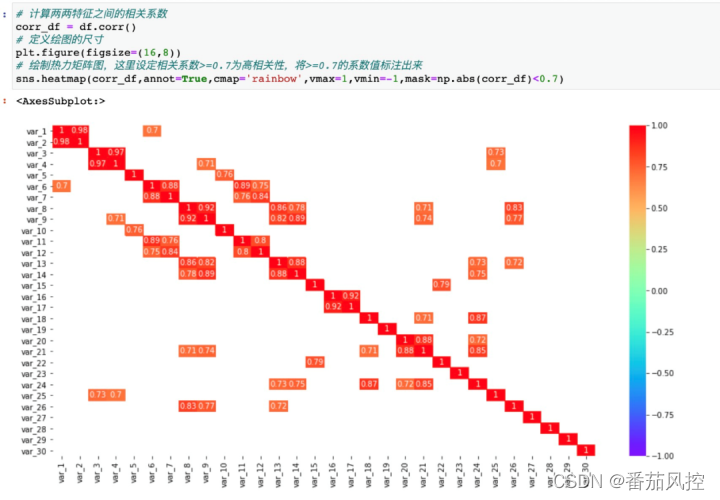
2.两两相关性的可视化,用pandas的corr()函数计算出两两特征之间的相关系数,然后通过seaborn的heatmap函数绘制相关性热力矩阵图。
?
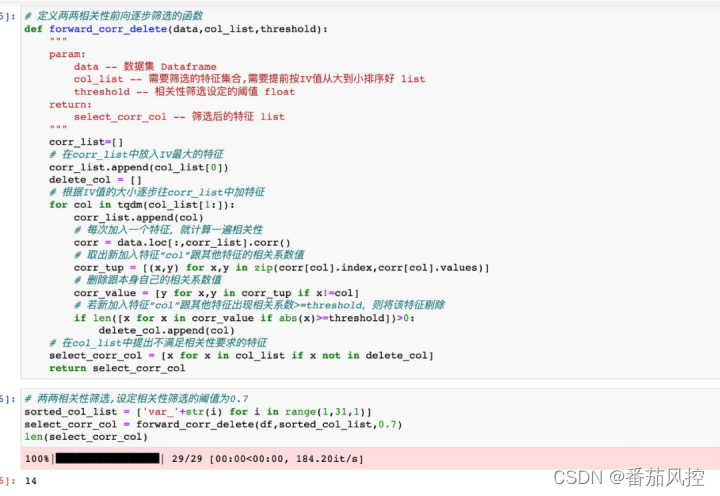
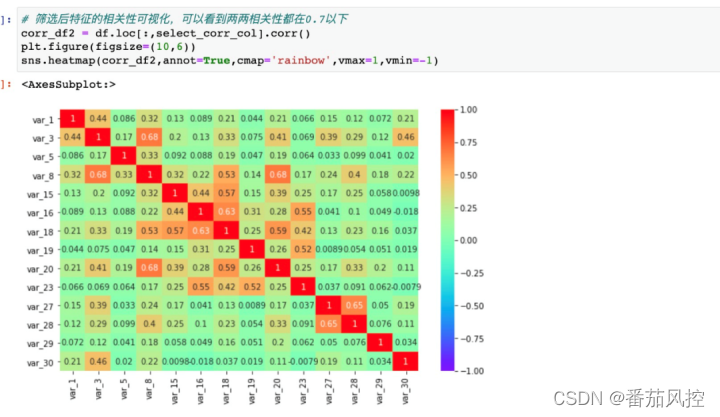
3.筛选方法采用前向选择的方法,先将特征按IV值进行从大到小排序(这里设定var_1到var_30 IV依次降低),先计算IV排名前两个var_1和var_2之间的相关性,若两者存在高相关性,则剔除var_2,然后按顺序依次添加特征,每次添加都要判断新加入的特征与其他特征是否存在高相关性,若存在则剔除,若不存在则保留,直到添加完所有的特征。
?
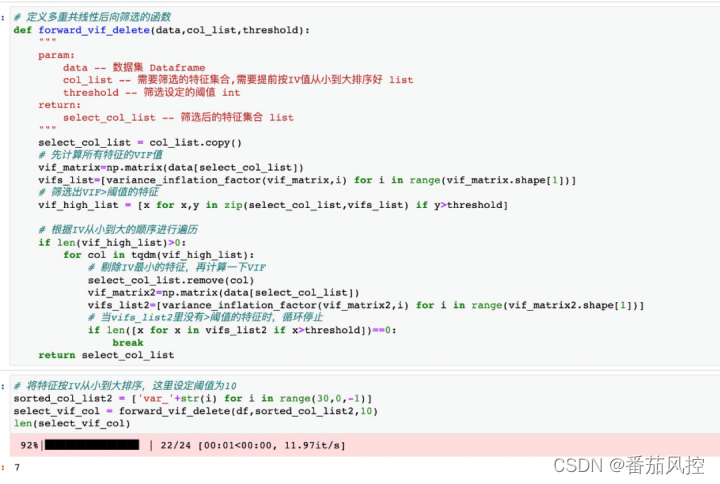
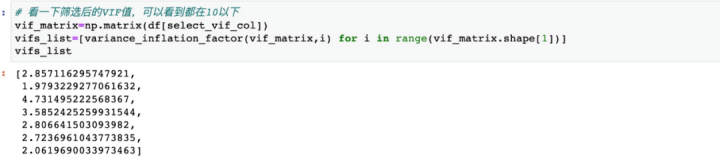
4.筛选方法采用后向选择的方法,先用全部特征计算出每个特征的VIF值,然后从中挑选出VIF>阈值的特征,然后将VIF>阈值的特征按IV从小到大进行遍历,先剔除IV最小的那一个,然后再计算一下剩下特征的VIF值,若VIF都小于阈值,则循环停止,否则继续剔除特征,直到不出现VIF>阈值的特征。
?
以上完整版本内容欢迎星球同学移步到知识星球查收完整内容:
?
其中本文相关的数据集跟代码也欢迎参考本次上传到知识星球的内容:2022年3月1日的【星球打榜答案】与【星球打榜作业】:
~原创文章
…
end