[人工智能][动手学深度学习] 03 多层感知机

1.多层感知机

多层感知机(multilayer perceptron)通常被称作MLP，也叫做深度前馈网络。
多层感知机中的多层体现在，在之前的先行神经网络中添加了一个隐藏层。
如下图所示：

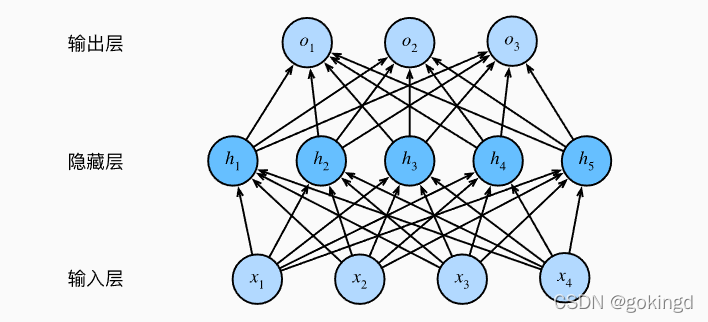
这是一个两层的神经网络。其中的层数指的是神经元之间的权重参数。
多层感知机与线性神经网络非常类似：
假设有n个样本，样本有d维特征，则输入的神经元X为nxd的矩阵。
隐藏层权重W1为dxh的矩阵。这里的h指的是隐藏层神经元的个数。
则隐藏层输出为nxh的矩阵。同时要加上一个隐藏层的偏置b，1xh的向量。
再经过hxq的输出层权重W2，已经输出层偏置b，1xq的向量。这里的q是指的输出层神经元的个数。
$$H=X{W}^{(1)}+b^{(1)}$$
$$O=H{W}^{(2)+}+b^{(2)}$$
实际上，多层感知机是一个非线性模型。以上的表示形式并不是非线性的形式，两个权重向量合到一起，仍然是线性模型。多层感知机的非线性就体现在隐藏层的非线性激活函数。所以应该写为：
$$H=\sigma (X{W}^{(1)}+b^{(1)})$$
这样多层感知机就具有了更强的表达能力。

1.1 激活函数

非线性激活函数有很多种，常见的有：relu激活函数，sigmoid激活函数，tanh激活函数等等…
$$Relu(x)=max(0,x)$$
Relu激活函数有效地解决了反向传播中的梯度爆炸问题。Relu函数在0处不可微，但是它的表现效果仍然很好，部分原因是：神经网络训练算法通常不会达到代价函数的最小值，而是仅仅显著地减小它的值。
还有pRelu函数：
$$pRelu(x)=max(0,x)+\alpha min(0,x)$$

1.2 多层感知机的实现

import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
def load_data_fashion_mnist(batch_size,resize=None):
    trans = transforms.ToTensor()
    mnist_train = torchvision.datasets.FashionMNIST(root="../data",train=True,transform=
                                               trans,download=True)
    mnist_test = torchvision.datasets.FashionMNIST(root="../data",train=False,transform=trans,
                                              download=True)
    if resize:
        trans.insert(0,transforms.Resize(resize))
    trans = transforms.Compose(trans)
    return (data.DataLoader(mnist_train,batch_size,shuffle=True,
                            num_workers=get_dataloader_workers()),
           data.DataLoader(mnist_test,batch_size,shuffle=False,
                           num_workers=get_dataloader_workers))

num_inputs,num_outputs,num_hiddens = 784,10,256

W1 = nn.Parameter(torch.randn(num_inputs,num_hiddens,requires_grad=True)*0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens,requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens,num_outputs,requires_grad=True)*0.01)
b2 = nn.Parameter(torch.zeros(num_outputs,requires_grad=True))

parmas = [W1,b1,W2,b2]
          
def relu(x):
    a = torch.zeros_like(x)
    return torch.max(x,a)   

def net(X):
    X=X.reshape((-1,num_inputs))
    H = relu(X@W1+b1)
    return (H@W2+b2)

loss = nn.CrossEntropyLoss()
          
num_epochs,lr =10,0.1
updater = torch.optim.SGD(parmas,lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,updater)

2. 正则化

当模型在训练数据集上表现得很好，但是在测试数据集上却表现得泛化能力很差，就是出现了过拟合。通常，可以降低模型复杂度、或者增强数据集、正则化等方式来解决过拟合问题。正则化类似于优化问题，在深度学习中占有很高的地位。
对于之前的线性模型、和多层感知机等，我们可以通过限制参数值得选择范围来控制模型容量。类似于优化问题：
$$minl(w,b)s.t.||w|{|}^2\le \theta$$

2.1 范数

p范数： $||x|{|}_p=\sqrt[p]{{\sum }_i|x_i{|}^p}$
0范数： 表示向量中非0元素得个数。
1范数： 表示向量中所有元素的绝对值之和
2范数：表示向量元素的平方和开根号

2. 2 1范数与2范数正则化

为了解决过拟合问题，通常在损失函数中加入1范数或2范数。
2范数正则化：
$$minl(w,b)+\frac{\lambda }{2}||w|{|}^2$$
Q:如何理解正则化能够解决过拟合问题？
A: 通俗地直观地理解就是：模型在训练时，训练数据太少，模型记住了所有的数据，来了一个不认识的数据时，模型就不知道怎么分类了。而正则化就是在损失函数后面加一项，来增大训练误差来减少测试误差的一种策略。换句话说：我们只想要模型记住数据集中有用的特征，而不是所有的特征。
以上面的2范数正则化为例：我们想要通过w的大小来降低模型的复杂度，这时就在后面加入一个正则项，正则项是关于w的函数，以及超参数$\lambda$的函数。这时，在梯度下降时，就需要权衡前一项和后一项，来达到一个平衡，这样就控制了w不会变得特别大。可以看一张经典的图：

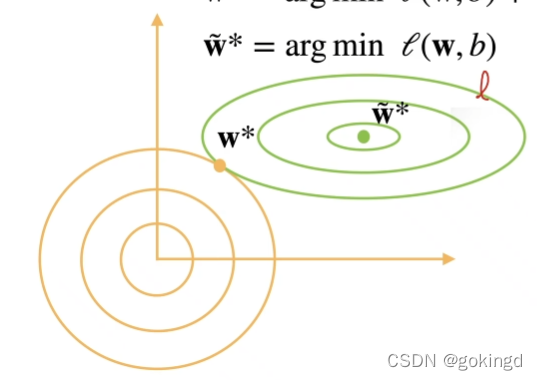
同时，$\lambda$超参数控制了正则项的重要程度。如果$\lambda =0$，显然正则项就没有用，如果$\lambda ?>\infty$,则w的值就会趋于0.
Q: 那为什么l1范数和l2范数能达到这样的效果呢？
A: 1范数，又被称为lasson regression。l1范数的作用是能求得稀疏的解。直观感受就是，上图中的同心圆换成一个正方形，只有边上很少的点是稀疏的。解是稀疏的，就意味着有不少的系数是为0，这样就达到了筛选特征的效果，降低了模型的复杂度。
l2 范数在线性模型中又称为rigde regression ，岭回归。这里引用一句：L2范数惩罚项的加入使得$X^{T}X+\lambda I$满秩，保证了可逆，但是也由于惩罚项的加入，使得回归系数β的估计不再是无偏估计。所以岭回归是以放弃无偏性、降低精度为代价解决病态矩阵问题的回归方法。
单位矩阵I的对角线上全是1，像一条山岭一样，这也是岭回归名称的由来。
在加入l2范数正则化项后，梯度跟新就会变为：
$$W_{t+1}=(1?\eta \lambda )W_t?\eta \frac{?l(W_t,b_t)}{?W_t}$$
可以发现，与没有加入正则项的梯度下降损失函数相比，不同的就是Wt前面的系数，小于1了。这就是权重衰退。
所以l2范数通过权重衰退，抑制了模型中产生过拟合的参数，来防止了过拟合。

3. Dropout

Dropout是一种防止过拟合的方法。其原理是：一个好的模型需要对输入数据的扰动鲁棒，所以dropout就是在神经网络层中加入噪音。使用有噪音的数据等价于Tikhonov正则。所以Dropout本质还是一种正则化处理。
如何加入噪音呢呢？通常是以unbiased的方式加入噪音，是的加入之后的期望和之前的一样。一种做法是: 直接在输入后面加入正态分布的噪声。另一种更为广泛的做法是：在神经网络的某一层中加入Dropout层，也就是以概率p来舍去这一层的某些结点，剩下的结点就扩大1-p倍，这样总体的期望还是不变的。
h ′ = { h 1 ? p ? o t h e r w i s e 0 ? 概 率 p h^{'}=\{^{0 \ 概率p}_{\frac{h}{1-p} \ otherwise} h′={1?ph??otherwise0?概率p?

3.1 简单实现

import torch
from torch import nn
from d2l import torch as d2l
num_inputs,num_outputs,num_hiddens,num_hiddens2=784,10,256,256
dropout1,dropout2=0.2,0.5
net = nn.Sequential(
    nn.Flatten(),
    nn.Linear(784,256),
    nn.ReLU(),
    nn.Dropout(dropout1),
    nn.Linear(256,256),
    nn.ReLU(),
    nn.Dropout(dropout2),
    nn.Linear(256,10)
)

def init_weights(m):
    if type(m)==nn.Linear:
        nn.init.normal_(m.weight,std=0.01)
        
net.apply(init_weights)

trainer = torch.optim.SGD(net.parameters(),lr=lr)

d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)

Reference

https://zh-v2.d2l.ai/
深度学习 Ian Goodfellow等 2017 人民邮电出版社