文章目录
一、神经网络
1.神经网络例子
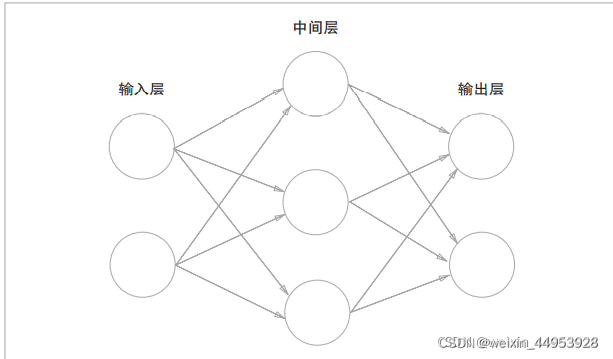
2.三层神经网络
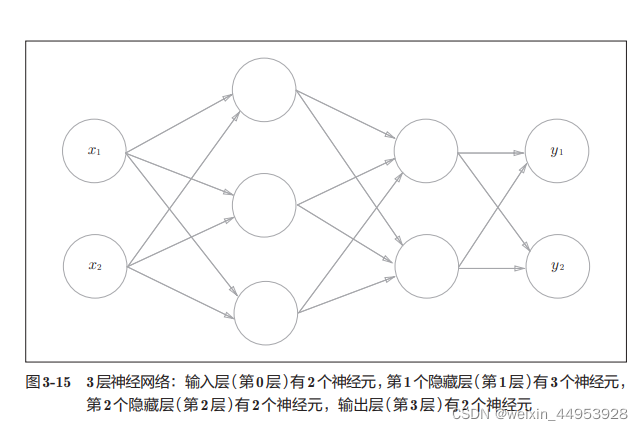
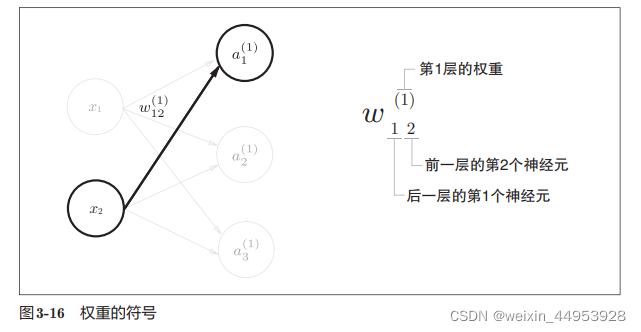
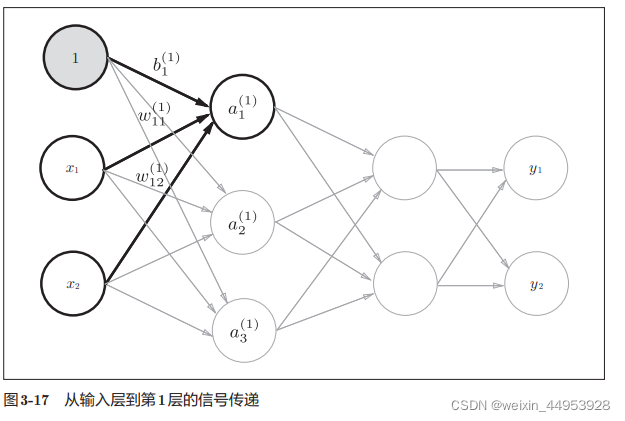
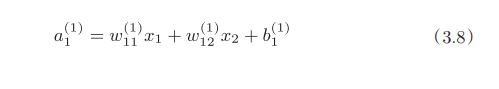

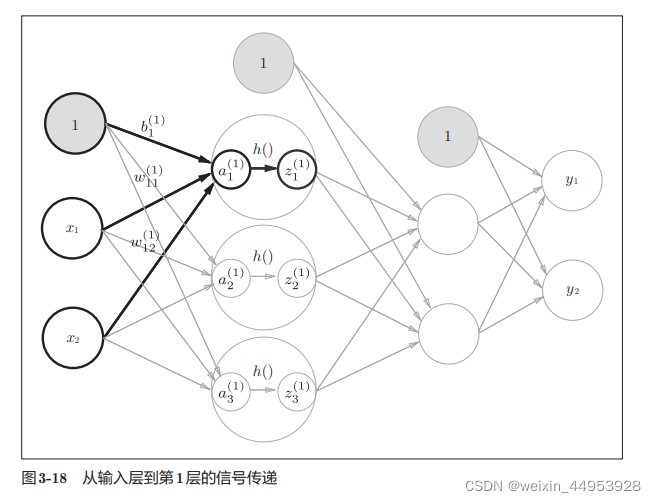
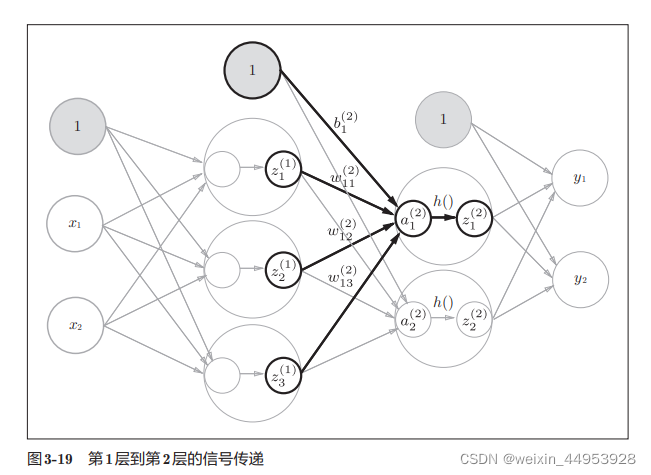
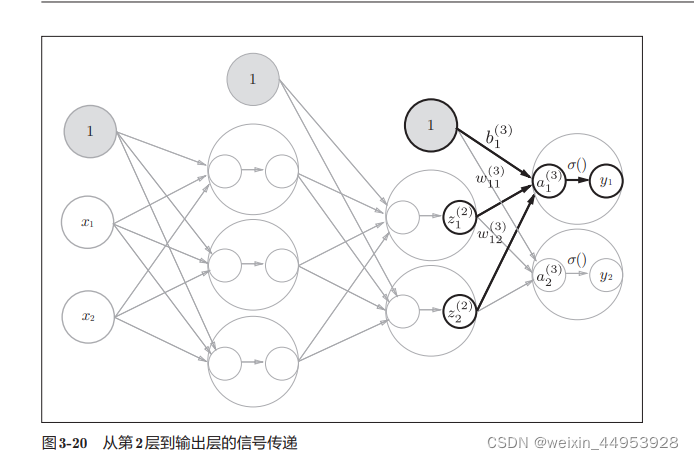
二、softmax回归模型
1.softmax函数

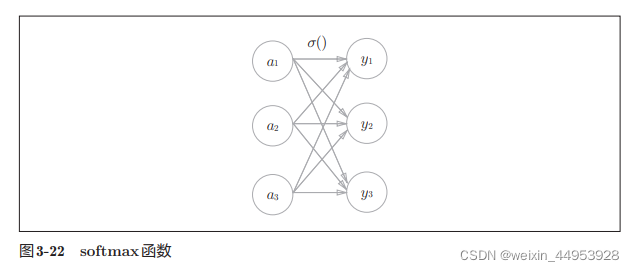
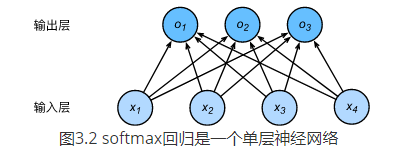
2.例子
o 1 = x 1 w 11 + x 2 w 21 + x 3 w 31 + x 4 w 41 + b 1 , o 2 = x 1 w 12 + x 2 w 22 + x 3 w 32 + x 4 w 42 + b 2 , o 3 = x 1 w 13 + x 2 w 23 + x 3 w 33 + x 4 w 43 + b 3 . \begin{aligned}o_1 &= x_1 w_{11} + x_2 w_{21} + x_3 w_{31} + x_4 w_{41} + b_1,\\o_2 &= x_1 w_{12} + x_2 w_{22} + x_3 w_{32} + x_4 w_{42} + b_2,\\o_3 &= x_1 w_{13} + x_2 w_{23} + x_3 w_{33} + x_4 w_{43} + b_3.\end{aligned} o1?o2?o3??=x1?w11?+x2?w21?+x3?w31?+x4?w41?+b1?,=x1?w12?+x2?w22?+x3?w32?+x4?w42?+b2?,=x1?w13?+x2?w23?+x3?w33?+x4?w43?+b3?.?
y
^
1
,
y
^
2
,
y
^
3
=
softmax
(
o
1
,
o
2
,
o
3
)
\hat{y}_1, \hat{y}_2, \hat{y}_3 = \text{softmax}(o_1, o_2, o_3)
y^?1?,y^?2?,y^?3?=softmax(o1?,o2?,o3?)
y
^
1
=
exp
?
(
o
1
)
∑
i
=
1
3
exp
?
(
o
i
)
,
y
^
2
=
exp
?
(
o
2
)
∑
i
=
1
3
exp
?
(
o
i
)
,
y
^
3
=
exp
?
(
o
3
)
∑
i
=
1
3
exp
?
(
o
i
)
.
\hat{y}_1 = \frac{ \exp(o_1)}{\sum_{i=1}^3 \exp(o_i)},\quad \hat{y}_2 = \frac{ \exp(o_2)}{\sum_{i=1}^3 \exp(o_i)},\quad \hat{y}_3 = \frac{ \exp(o_3)}{\sum_{i=1}^3 \exp(o_i)}.
y^?1?=∑i=13?exp(oi?)exp(o1?)?,y^?2?=∑i=13?exp(oi?)exp(o2?)?,y^?3?=∑i=13?exp(oi?)exp(o3?)?.
三、激活函数
1.sigmoid函数

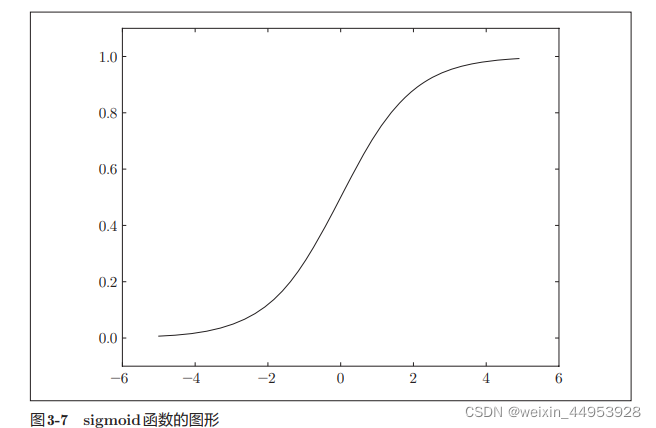
2.阶跃函数


3.ReLU激活函数
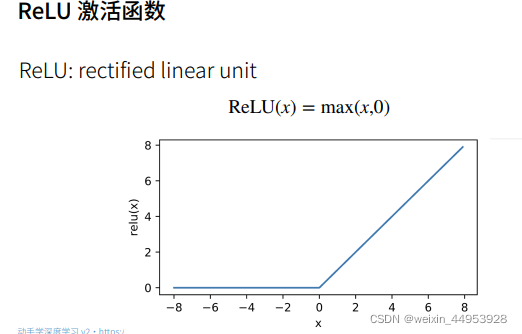
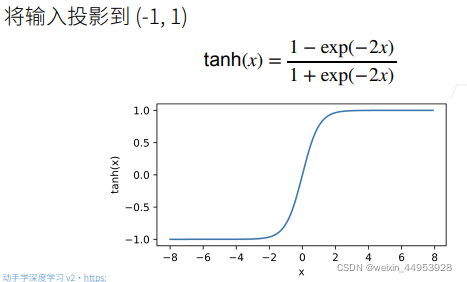
4、Tanh 激活函数
四、损失函数
1.均方误差

2.交叉熵误差
