目的

step1 收益波动率和夏普比率的计算是基于收益率是正态分布的假设
step2 为什么收益率正态分布会让收益和风险计算比较容易？
如果收益率的分布可以用正态分布来近似拟合的话，投资管理将变得更加容易
1). 当风险收益对称时，标准差是一个很好的衡量标准
2). 如果各个资产的收益具有正态分布，那么其组成的投资组合的收益也服从正态分布
3). 可以仅适用均值和标准差来估计未来的情境
step3 收益率的分布偏离正态分布怎么办？
此时，
1). 标准差不再是一个衡量风险的完美度量工具
2). 夏普比率不再是证券表现的完美度量工具
因此，
需要考虑偏度和峰度

概念

1. 偏度(Skewness)用来度量随机变量概率分布的不对称性
偏度取值范围为(负无穷,正无穷)
当偏度<0，概率分布左偏
当偏度=0, 表示数据相对均匀的分布在平均值两侧，不一定是绝对的对称分布
当偏度>0, 概率分布右偏
2. 峰度(Kurtosis)用来度量随机变量概率分布的陡峭程度
峰度取值范围为[1,正无穷),完全服从正态分布的数据的峰度值为3，峰度值越大，概率分布图越高尖；峰度值越小，越矮胖
3. 假设检验：检验是否服从正态分布
3.1 假设H0:是正态分布【这个是期望的结果】；HA:不是正态分布
3.2 Jarque Bera是用来检验正态分布【要求样本数在2000个以上】
3.3 置信区间
1). 设置99%的置信区间，表示有99%的信心认为结果是正态分布。
2). 剩余的1%叫做显著性水平
3). 如果置信区间设置为99%,显著水平就是1%;如果置信区间设置为95%,显著性水平就是5%。检验要求越严格，显著性水平就越小，例如医药行业一般设为1%,银行做风险可行性会将显著性水平设置小于1%
4. 看结果p-value值，p-value值越小越拒绝
p<1%，拒绝原假设，结果：不是正态分布
p>1%，接受原假设，结果：是正态分布

先贴结果

偏度:0.017862413071976304 峰度:0.0006589607625819838 检验p值:pvalue=0.501752635804537 检验结果:是正态分布	偏度:-1.0986798779690312 峰度:14.776922600537802 检验p值:pvalue=0.0 检验结果:不是正态分布	偏度:-1.4275663167447816 峰度:26.921066302426375 检验p值:pvalue=0.0 检验结果:不是正态分布

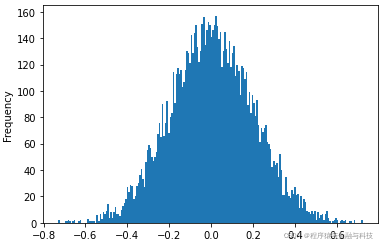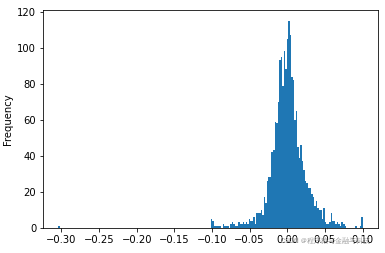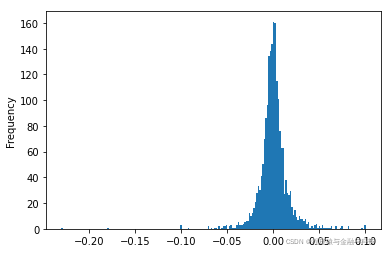?代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
df_004 = pd.read_csv('600004.csv',encoding='utf-8')
df_004['tradeDate'] = pd.to_datetime(df_004['tradeDate'])
df_004.set_index('tradeDate',inplace=True)
df_004['ret'] = df_004['closePrice'].pct_change()
df = df_004.iloc[-2016:]
df['ret'].plot.hist(bins=200)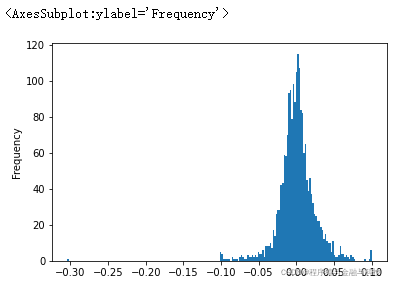

# 偏度 bias=False不自动纠正
ss.skew(df['ret'],bias=False)
# out: -1.0986798779690312

# 峰度 bias=False不自动纠正
ss.kurtosis(df['ret'],bias=False)
# out: 14.776922600537802

# 检验是否正态分布
ss.jarque_bera(df['ret'])
# out: Jarque_beraResult(statistic=18648.83420095886, pvalue=0.0)

df_015 = pd.read_csv('600015.csv',encoding='utf-8')
df_015['tradeDate'] = pd.to_datetime(df_015['tradeDate'])
df_015.set_index('tradeDate',inplace=True)
df_015['ret'] = df_015['closePrice'].pct_change()
df02 = df_015.iloc[-2016:]
df02['ret'].plot.hist(bins=200)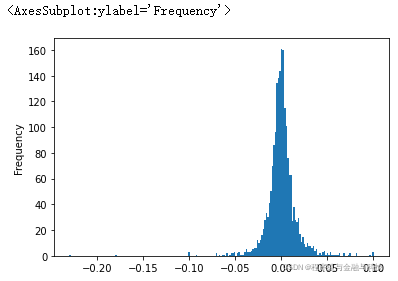

# 偏度 bias=False不自动纠正
ss.skew(df02['ret'],bias=False)
# out: -1.4275663167447816

# 峰度 bias=False不自动纠正
ss.kurtosis(df02['ret'],bias=False)
# out: 26.921066302426375

# 检验是否正态分布
ss.jarque_bera(df02['ret'])
# out: Jarque_beraResult(statistic=61247.39825308066, pvalue=0.0)

# 生成一个正态分布
normal_numbers = pd.Series(np.random.normal(0,0.2,10000))
ss.skew(normal_numbers ,bias=False)
# out: 0.017862413071976304
ss.kurtosis(normal_numbers,bias=False)
# out: 0.0006589607625819838
ss.jarque_bera(normal_numbers)
# out: Jarque_beraResult(statistic=1.379296076193386, pvalue=0.501752635804537)
normal_numbers.plot.hist(bins=200)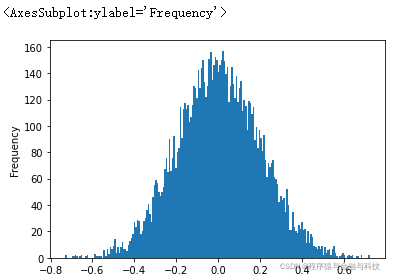

?将检验是否为正态分布写成一个函数

import scipy
def is_normal(r,level=0.01):
    '''
    对一个Series实施Jarque-Bera检验，默认显著性水平为1%
    若p值大于显著性水平，则无法拒绝原假设(正态分布)
    返回True 表明该Series是正态分布
    '''
    if isinstance(r,pd.DataFrame):
        return r.aggregate(is_normal)
    else:
        test_statistic,p_value = scipy.stats.jarque_bera(r)
        return p_value>level
is_normal(normal_numbers)
# out: True
is_normal(df['ret'])
# out: False
is_normal(df01['ret'])
# out: False