决策树的主要算法

构建决策树的关键：按照什么样的次序来选择变量（属性/特征）作为分类依据。
根据不同的目标函数，建立决策树主要有以下三种算法

ID3(J.Ross Quinlan-1975) 核心：信息熵，信息增益
C4.5——ID3的改进，核心：信息增益比/增益率
CART(Breiman-1984)，核心：基尼系数

ID3算法

由Ross Quinlan在1986年提出，ID3决策树可以有多个分支，但是不能处理特征值为连续的情况，根据“最大信息熵增益”选取当前最佳的特征来分割数据。

香农熵(Shannon Entropy)

熵用来表示事件的不确定性，熵越小代表事件发生的概率就越大。若熵为0，表示事件百分百发生。
对于常见分类系统来说，假设类别D是变量，D可能取值D₁，D₂…D_n，每个类别出现的概率为P(D₁),P(D₂)…P(D_n),共n类。
分类系统的熵为：
$H(D)=-\sum_{i=1}^{n}P(D_{i})\ast log_{2}P(D_{i})$
当我们的概率是由数据统计得到时，此时的熵称为经验熵（empirical entropy）。
举个例子：
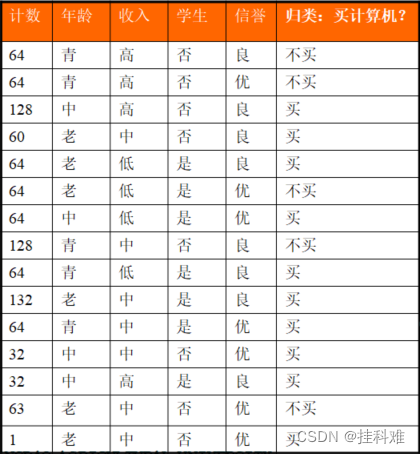
在这里插入图片描述
我们先不考虑特征，该样本最终分为结果只有买与不买两类，根据统计可知在1024个样本中有641个数据结果为买，383个数据结果为不买。显然买的概率为(641/1024),不买的概率为(383/1024)。显然这两个概率是我们统计得到的，通过这两个统计得到的概率计算的熵称为经验熵，为：
$H(D)=-\frac{641}{1024}*log_{2}\frac{641}{1024}-\frac{383}{1024}*log_{2}\frac{383}{1024}=0.9537$
这就是我们第一步要做的，计算决策属性的熵。
该列中买与不买就是决策属性。

条件熵

条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。
$H(Y|X)=\sum_{j=1}^{n}p_{j}H(Y|X=x_{j})$
同样的，如果公式中的概率是由统计估计出来的话，这时的条件熵称为经验条件熵。
我们用H(D|A)表示在给定的特征A的条件下D的经验条件熵。假设特征A将D划分为v个子集{D₁,D₂,…D_v},例:年龄特征(A),将我们的数据集分成了三份{青年,中年,老年}.
此时条件熵为:

$H(D|A)=\sum_{j=1}^{v}\frac{|D_{j}|}{|D|}H(D_{j})=-\sum_{j=1}^{v}\frac{|D_{j}|}{|D|}\sum_{k=1}^{k}\frac{|D_{jk}|}{|D_{j}|} log_{2}\frac{|D_{jk}|}{|D_{j}|}$

信息增益(information gain)

计算完决策属性的熵以后，我们要根据信息增益来排序特征，那什么是信息增益呢？

信息增益是相对于特征而言的，表示得知特征A的信息而使得类Y的信息的不确定性减少的程度。信息增益越大，特征对最终的分类结果影响也就越大，因此此特征就被选上作为我们的分类特征。

简单地将，可以理解为一个特征对最终结果相关程度，信息增益大说明该特征与分类结果的关联性很强。特征的信息增益小，则说明该特征对分类的结果影响很小。

特征A信息增益( g(D,A) ) = 决策属性的熵 - 特征A的平均信息期望

定义为:
$g(D,A) = H(D) - E(D|A)$
上述已经计算了决策属性的熵,现在我们计算某个特征的平均熵期望.
年龄(A₁)将数据集为三个组:
青年(D₁),中年(D₂),老年(D₃)

我们把年龄为青年(D₁)的样本全都提取出来:
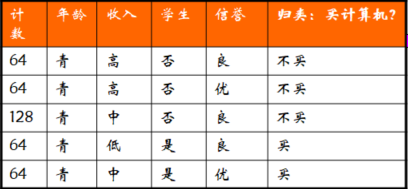
在这里插入图片描述
总共D₁=(64*4+128)384个样本,做以下定义
D₁₁(买)=128
D₁₂(不买)=256
青年中买与不买的概率:
P(D₁₁) = 128/384
P(D₁₂) = 256/384
根据分类熵的定义得:
$H(D_{1}) = -\sum_{i=1}^{n}P(D_{i})log_{2}P(D_{i})=-P(D_{11})log_{2}P(D_{11})-P(D_{12})log_{2}P(D_{12})=0.9183$
同理得到中年H(D₂)=0,老年H(D₃)=0.9175

青年组所占全部数据集比例(D₁) = 384/1024 = 0.375
中年组所占全部数据集比例(D₂) = 256/1024 = 0.25
老年组所占全部数据集比例(D₃) = 384/1024 = 0.375
得到年龄(A₁)的平均熵期望:
$E(D|A_{1})=\sum_{j=1}^{3}\frac{|D_{j}|}{|D|}H(D_{j})=0.375*0.9183+0.25*0+0.375*0.9157=0.6877$