NLP-统计分词-隐马尔可夫模型(维特比算法实现详解)
一、HMM模型
1. 模型状态集合
Q Q Q = { B B B, M M M, E E E, S S S}, N N N = 4
2. 观察状态集合
V V V = { 我 我 我, 爱 爱 爱, … } ,句子的集合。
3.观察状态和状态序列
观察序列:小 明 是 中 国 人
状态序列:
B
,
E
,
S
,
B
,
M
,
E
B, E, S, B, M, E
B,E,S,B,M,E
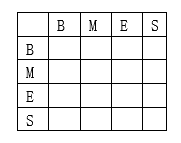
4. 状态转移概率分布矩阵
在中文分词中就是状态序列
Q
Q
Q = {
B
B
B,
M
M
M,
E
E
E,
S
S
S} 的转移概率,这个状态概率矩阵是在训练阶段参数估计中得到。
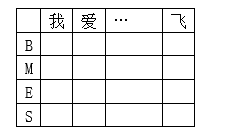
5. 观测状态概率矩阵(发射概率)
在中文分词中发射概率指的是每一个字符对应状态序列
Q
Q
Q = {
B
B
B,
M
M
M,
E
E
E,
S
S
S} 中每一个状态的概率,通过对训练集每个字符对应状态的频数统计得到。
6. 初始概率
在中文分词初始状态概率指的是每一句话第一个字符的对应状态概率。
{
B
B
B:xxx,
M
M
M: xxx,
E
E
E: xxx,
S
S
S: xxx}
7. 目标

max =
m
a
x
P
(
i
1
,
i
2
,
i
3
.
.
.
,
i
T
∣
o
1
,
o
2
,
o
3
.
.
.
,
o
T
)
maxP(i_1, i_2, i_3...,i_T | o_1,o_2,o_3... ,o_T)
maxP(i1?,i2?,i3?...,iT?∣o1?,o2?,o3?...,oT?)
其中:
T
T
T 为句子长度,
o
i
o_i
oi? 是句子的每一个字,
i
i
i_i
ii? 是每个字的标记。
根据贝叶斯公式:
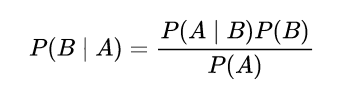
P
(
i
∣
o
)
P(i | o)
P(i∣o) =
P
(
o
∣
i
)
P
(
o
)
P(o | i) P(o)
P(o∣i)P(o) /
P
(
i
)
P(i)
P(i)
根据齐性HMM:
P
(
o
)
=
p
(
o
1
)
p
(
o
2
∣
o
1
)
.
.
.
p
(
o
t
∣
o
t
?
1
)
P(o) = p(o1)p(o_2| o_1)...p(o_{t}| o_{t-1})
P(o)=p(o1)p(o2?∣o1?)...p(ot?∣ot?1?), 状态转移概率。
P
(
o
∣
i
)
=
p
(
o
1
∣
i
1
)
.
.
.
p
(
o
t
∣
i
t
)
P(o | i) = p(o_1| i_1)...p(o_{t}| i_{t})
P(o∣i)=p(o1?∣i1?)...p(ot?∣it?) , 即观测状态生成的概率(发射概率)。
使 P P P = P ( o ∣ i ) P ( o ) P(o | i) P(o) P(o∣i)P(o) = P ( o 1 ) P ( o 1 ∣ i 1 ) ∏ 2 T P ( o i ∣ o i ? 1 ) P ( o i ∣ i i ) = P(o_1)P(o_1|i_1)∏{_2^T}P(o_i|o_{i-1})P(o_i|i_i) =P(o1?)P(o1?∣i1?)∏2T?P(oi?∣oi?1?)P(oi?∣ii?)概率最大。
二、python实现
1.模型参数初始化

2.求解过程
P = P ( o 1 ) P ( o 1 ∣ i 1 ) ∏ 2 T P ( o i ∣ o i ? 1 ) P ( o i ∣ i i ) P = P(o_1)P(o_1|i_1)∏{_2^T}P(o_i|o_{i-1})P(o_i|i_i) P=P(o1?)P(o1?∣i1?)∏2T?P(oi?∣oi?1?)P(oi?∣ii?)
求 “我” 分别是 B B B、 M M M、 E E E、 S S S的概率: P ( o 1 ) P ( o 1 ∣ i 1 ) P(o_1)P(o_1|i_1) P(o1?)P(o1?∣i1?)

V
V
V: 第一个字典记录开始的
B
B
B、
M
M
M、
E
E
E、
S
S
S概率
p
a
t
h
path
path:记录当前状态

求 “我” 的每个状态到 “爱”每个状态的概率: ∏ 2 T P ( o i ∣ o i ? 1 ) P ( o i ∣ i i ) ∏{_2^T}P(o_i|o_{i-1})P(o_i|i_i) ∏2T?P(oi?∣oi?1?)P(oi?∣ii?)


y
y
y 记录下一个状态,遍历 “我” 的每一个状态,由
y
0
y_0
y0?记录。
遍历结束会生成四个 (概率,字典索引)的列表:
[
(
p
r
o
b
,
s
t
a
t
e
)
,
(
p
r
o
b
,
s
t
a
t
e
)
,
(
p
r
o
b
,
s
t
a
t
e
)
,
(
p
r
o
b
,
s
t
a
t
e
)
]
[(prob, state), (prob, state), (prob, state), (prob, state)]
[(prob,state),(prob,state),(prob,state),(prob,state)]
寻找概率最大的路径,新的路径 = path[state] (之前的路径) + B
运行结果如下,选择S 到 B 的路径:


循环遍历,到“爱” 的最终路径如下:

