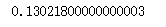[人工智能]11.EM算法、HMM模型

EM算法入门

算法介绍

极?似然估计

EM算法实例描述

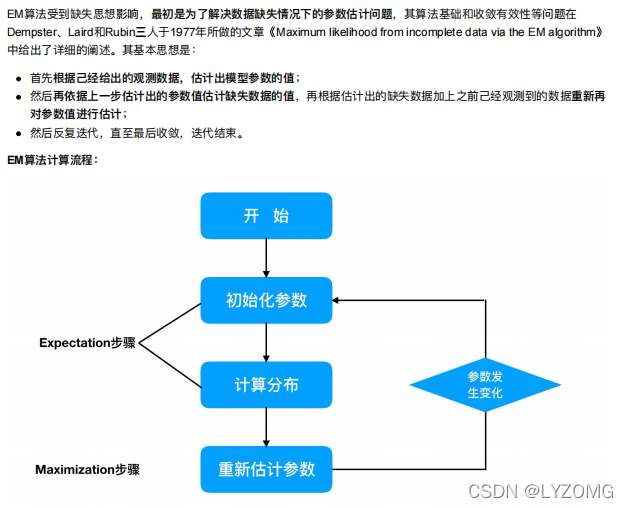
EM算法流程

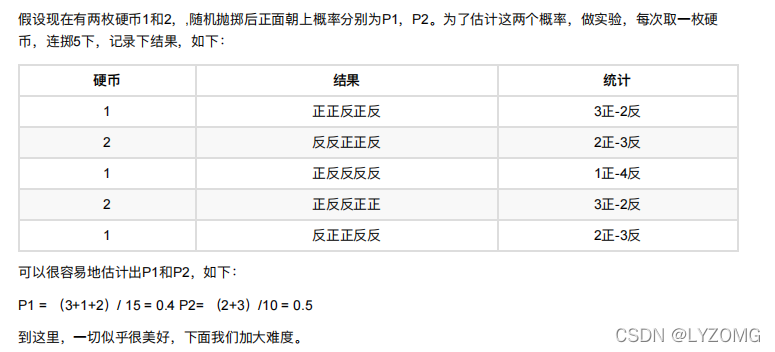
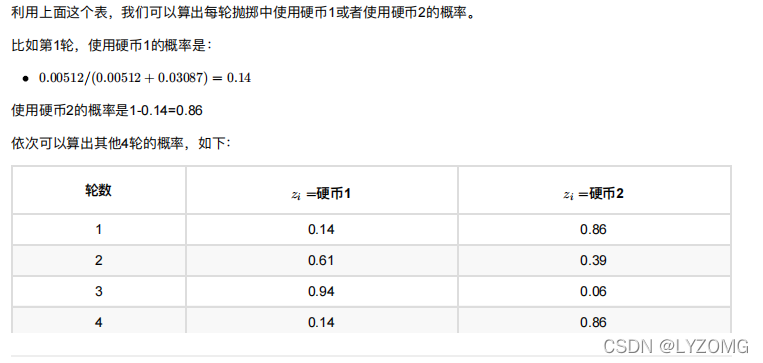
EM算法实例

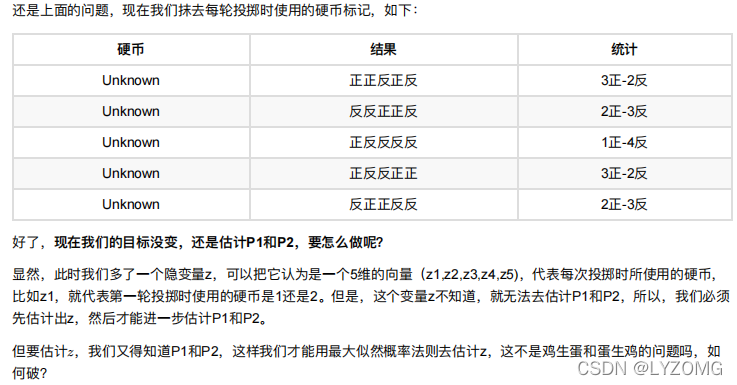
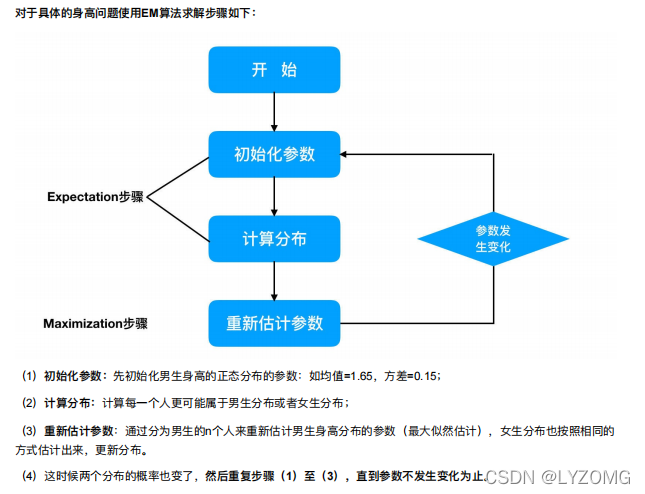
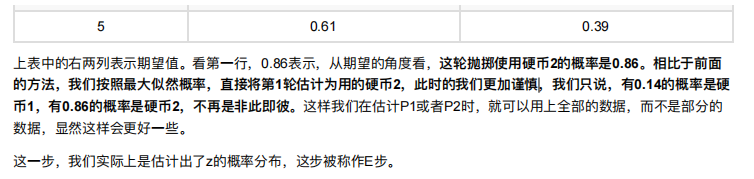
EM初级版

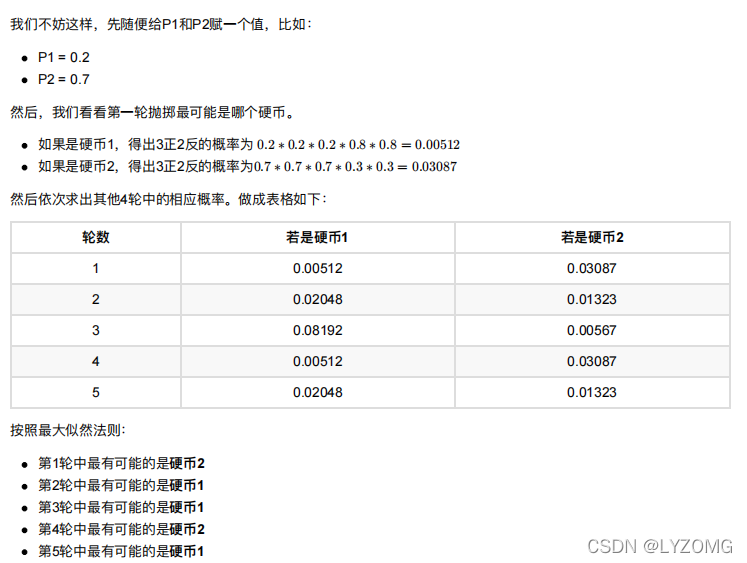
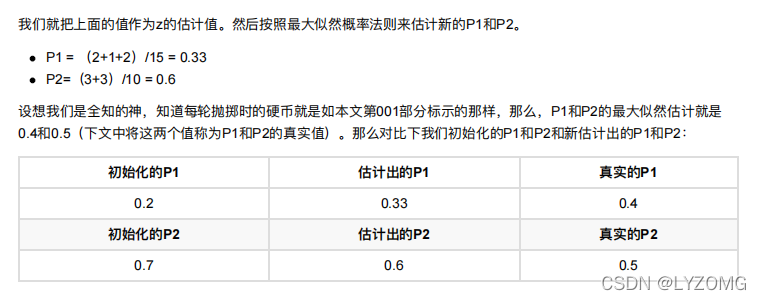
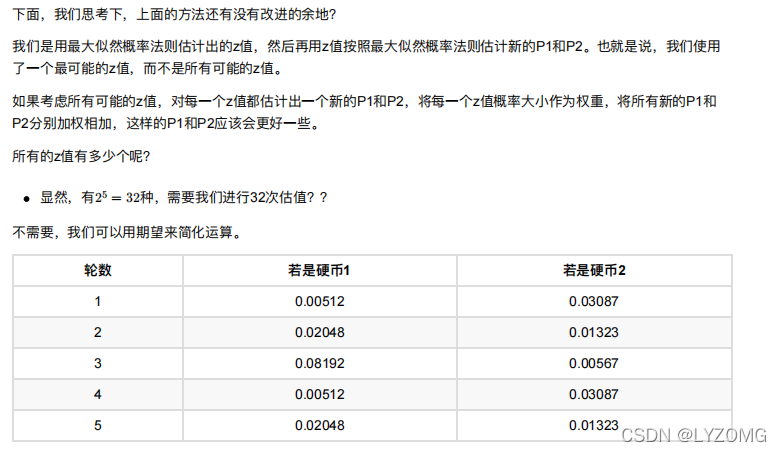
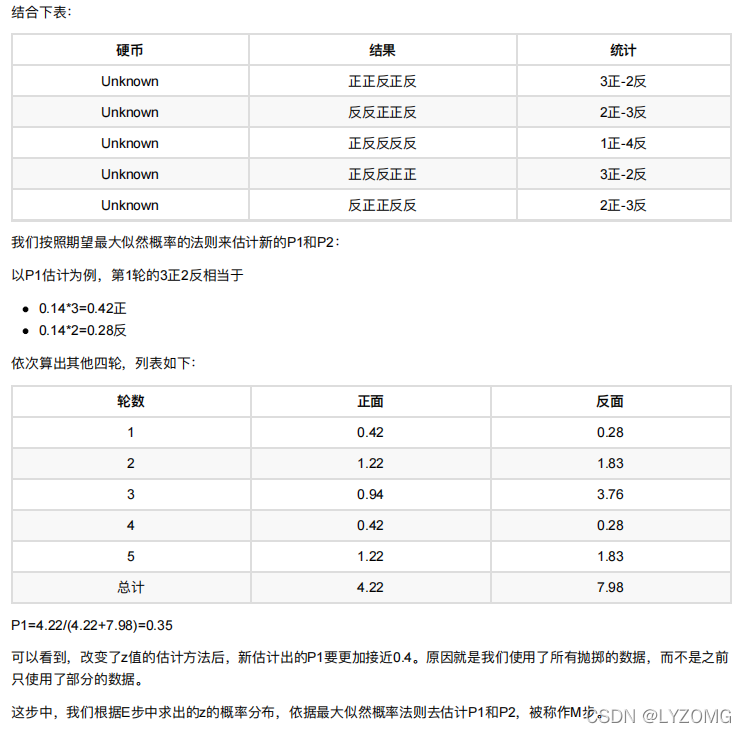
EM进阶版

HMM模型入门

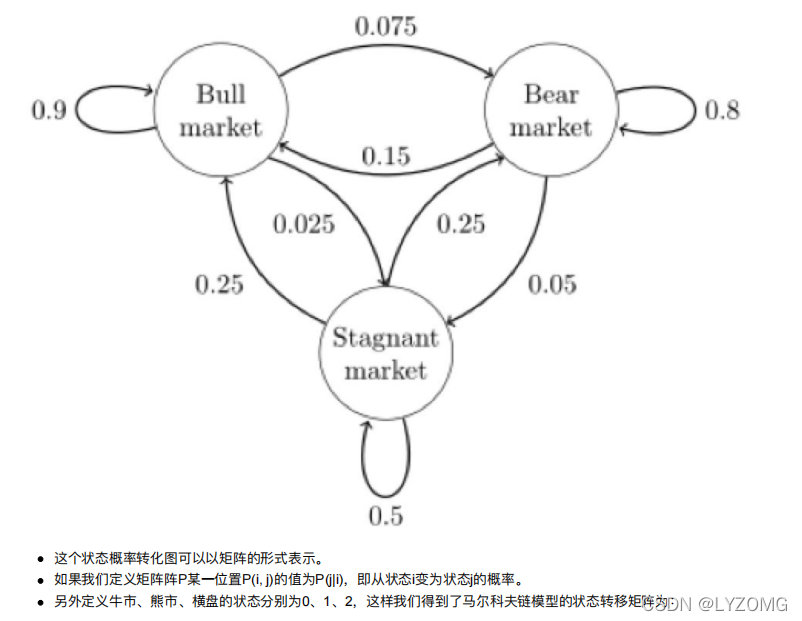
马尔科夫链

?尔科夫链即为状态空间中从?个状态到另?个状态转换的随机过程。

例子

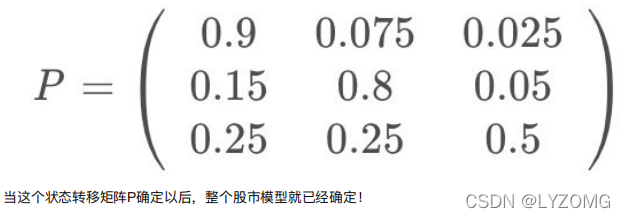
HMM简介

例子

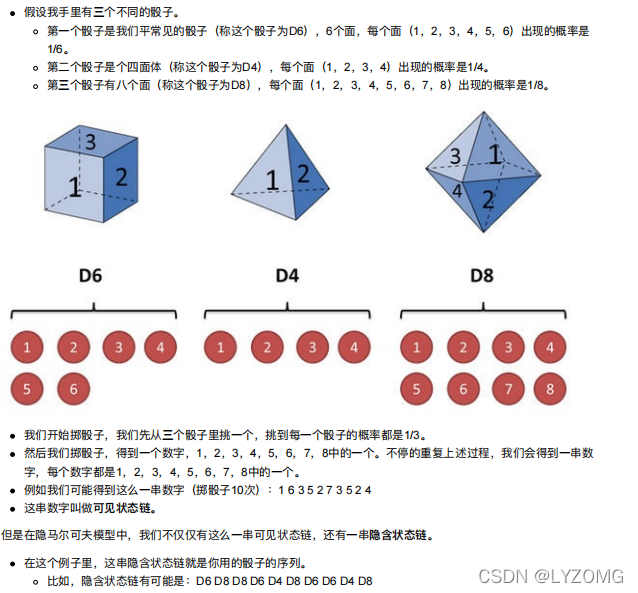
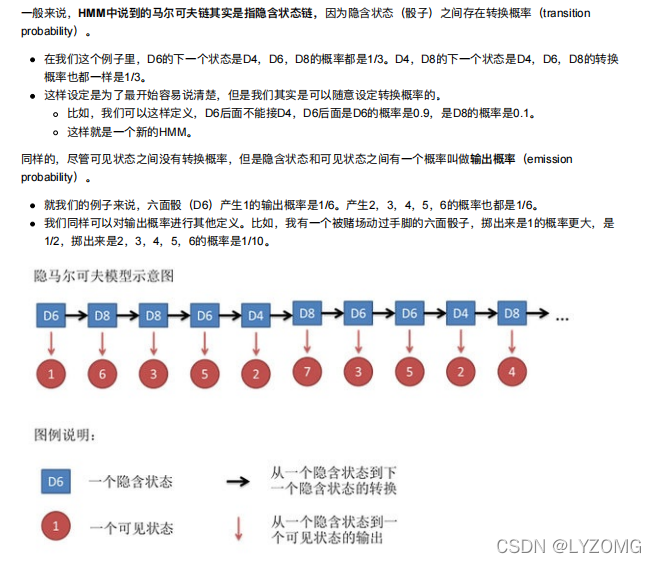
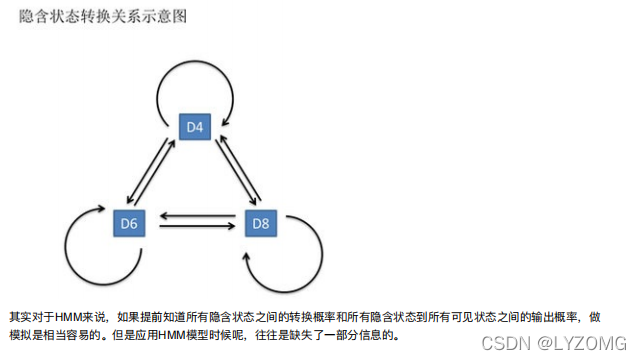
例子进阶

解决问题二

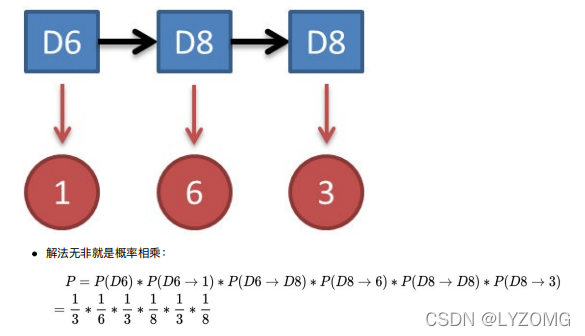
解决问题一

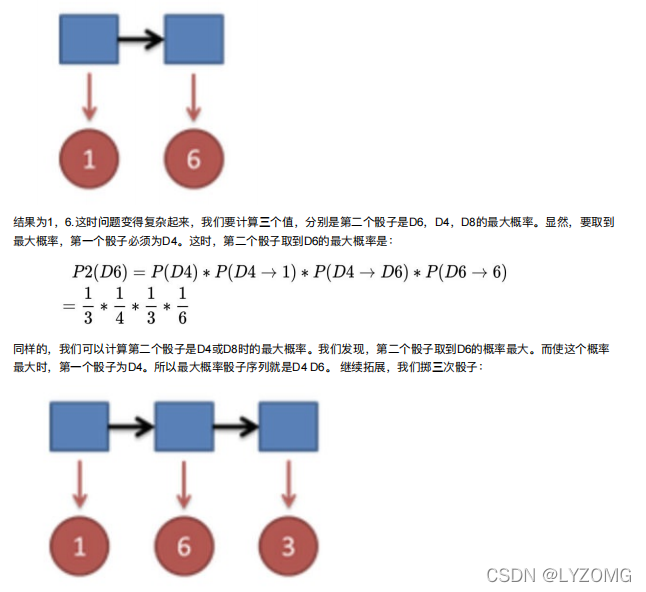
解决问题三

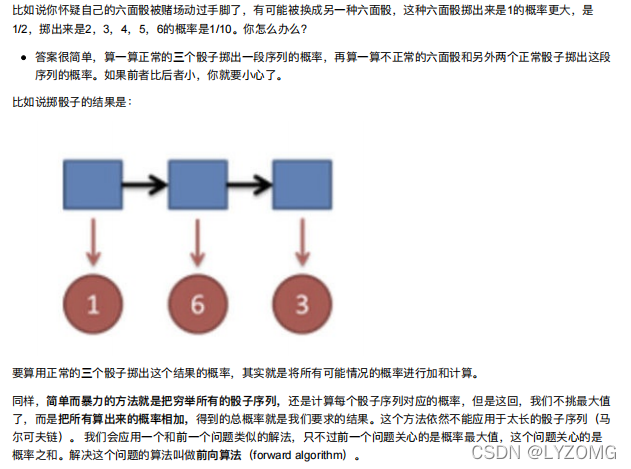
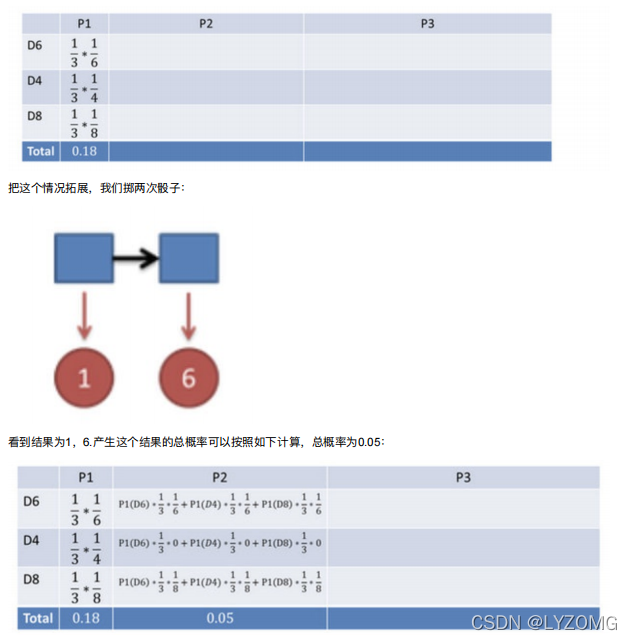
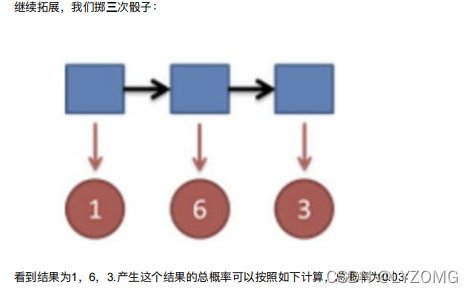
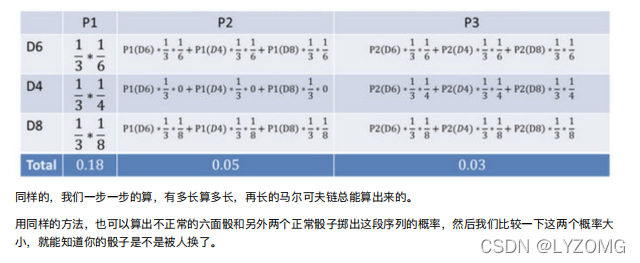
HMM模型基础

定义

?次?尔科夫链假设

观测独?性假设

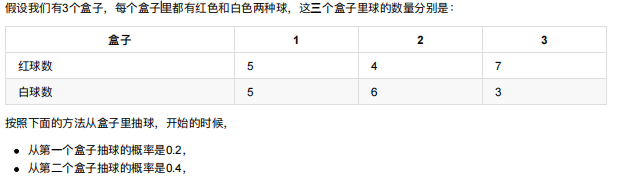
HMM模型实例

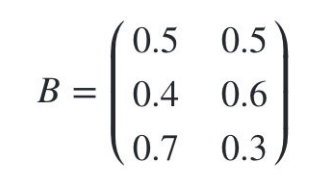
HMM观测序列的?成

HMM模型的三个基本问题

前向后向算法评估观察序列概率

前向后向算法是前向算法和后向算法的统称，这两个算法都可以?来求HMM观测序列的概率

前向算法

算法总结

从递推公式可以看出，我们的算法时间复杂度是O(T N2)，?暴?解法的时间复杂度O(T NT )少了?个数量级。

例子

后向算法

熟悉了?前向算法求HMM观测序列的概率，现在我们再来看看怎么?后向算法求HMM观测序列的概率。 后向算法和前向算法?常类似，都是?的动态规划，唯?的区别是选择的局部状态不同，后向算法?的是“后向概率”。

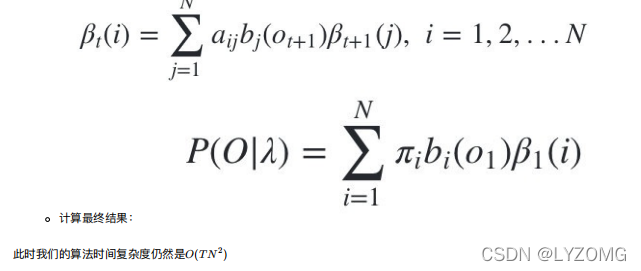
维特?算法解码隐藏状态序列

给定模型和观测序列，求给定观测序列条件下，最可能出现的对应 的隐藏状态序列。 HMM模型的解码问题最常?的算法是维特?算法，当然也有其他的算法可以求解这个问题。 同时维特?算法是?个通?的求序列最短路径的动态规划算法，也可以?于很多其他问题

HMM最可能隐藏状态序列求解概述

维特?算法概述

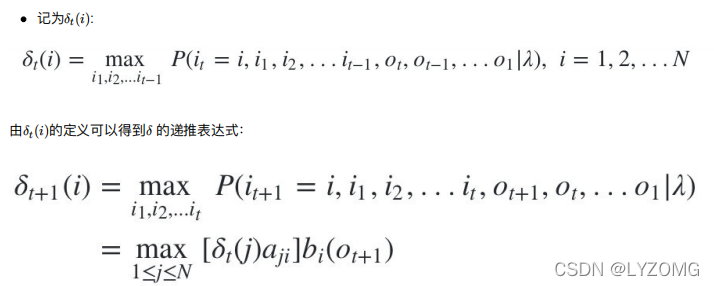
维特?算法流程总结

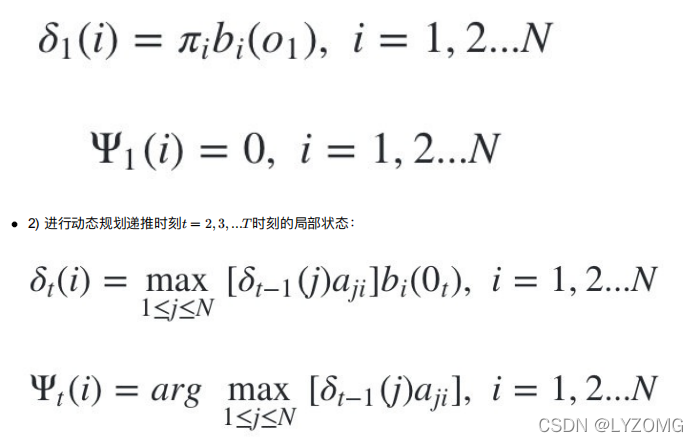
实例

鲍姆-?尔奇算法

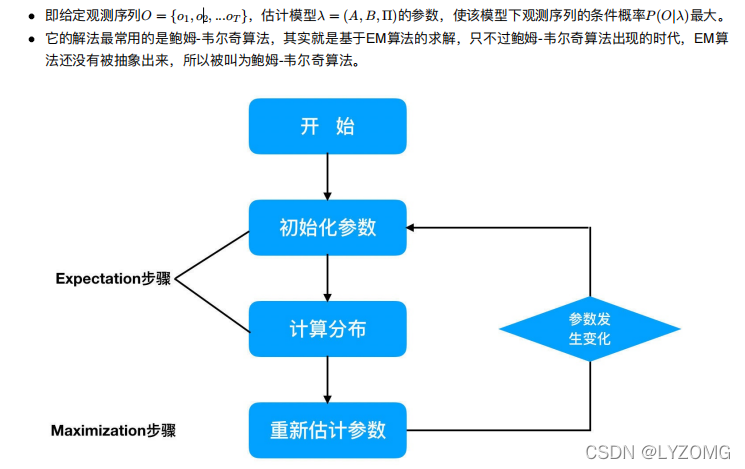
原理

HMM模型API

官网

pip3 install hmmlearn

hmmlearn介绍

MultinomialHMM实例

from hmmlearn import hmm
import numpy as np

# 设定隐藏状态的集合
states = ["box 1", "box 2", "box3"]
n_states = len(states)

# 设定观察状态的集合
observations = ["red", "white"]
n_observations = len(observations)

# 设定初始状态分布
start_probability = np.array([0.2, 0.4, 0.4])

# 设定状态转移概率分布矩阵
transition_probability = np.array([
  [0.5, 0.2, 0.3],
  [0.3, 0.5, 0.2],
  [0.2, 0.3, 0.5]
])

# 设定观测状态概率矩阵
emission_probability = np.array([
  [0.5, 0.5],
  [0.4, 0.6],
  [0.7, 0.3]
])

# 设定模型参数
model = hmm.MultinomialHMM(n_components=n_states)

# 设定初始状态分布
model.startprob_ = start_probability

# 设定状态转移矩阵
model.transmat_ = transition_probability

# 设定观测状态该路矩阵
model.emissionprob_ = emission_probability

# 设置观测序列值
seen = np.array([[0,1,0]]).T
seen

# seen 为二维数据，要先用flatten转换为一维
print("球的观测顺序为：\n",",".join(map(lambda x : observations[x],seen.flatten())))

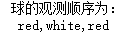
#  维特比 模型训练
box =  model.predict(seen)
box

在这里插入代码片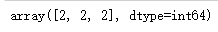

print("盒子最可能的隐藏状态顺序为：\n",",".join(map(lambda x : states[x],box.flatten())))

print("要注意的是score函数返回的是以?然对数为底的对数概率值，我们在HMM问题?中?动计算的结果是未取对数的原始 概率是0.13022,\n",model.score(seen))

import math

math.exp(model.score(seen))