[人工智能]二维svg图近似匹配

在此感谢所有愿意将自己的学习成果进行分享的博主，让我可以有中文资料参考（英语渣的痛谁懂…

二维ICP算法推导

py的svgpathtools的库可以实现读取svg图的关键点
https://www.cnpython.com/qa/342993

ICP算法的作用

通过旋转和平移，将两个对应点的距离尽可能的缩小。

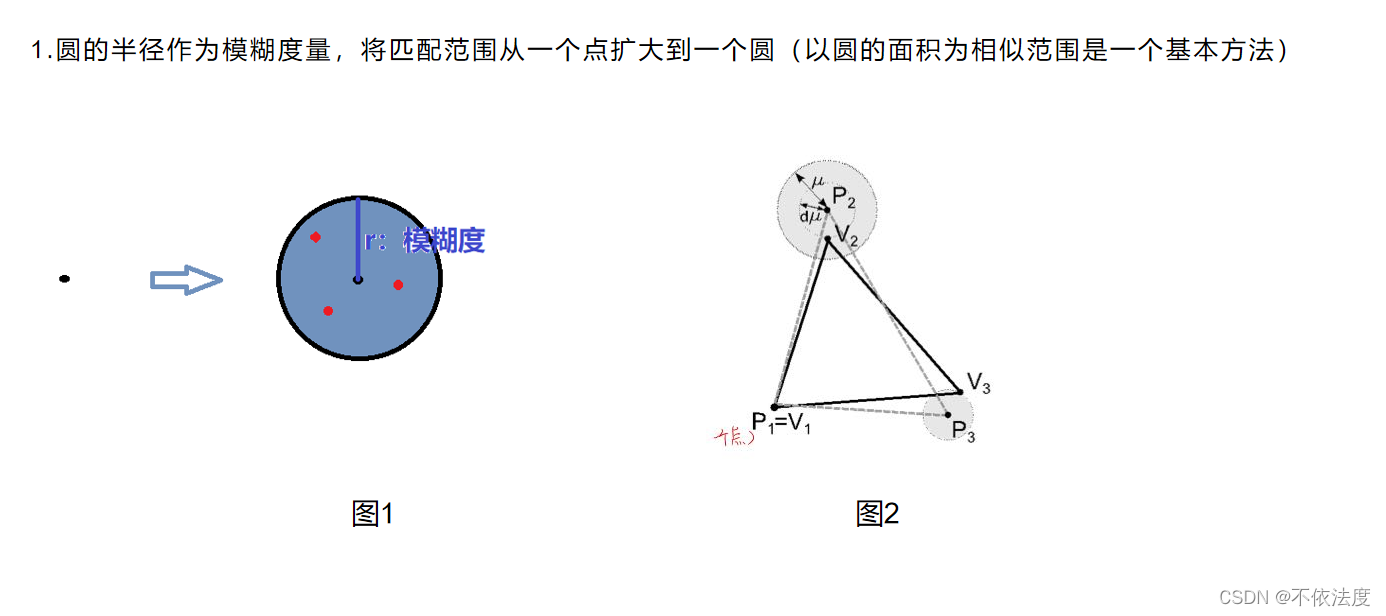
先用图解释一下二维ICP工作原理

计算欧式距离最近的两点被认为是对应点，那么我们就将两个点云中的任意两点进行匹配，让匹配后的对应点之间的距离累加最小。

1.我们初始载入图片，获取图的关键点（初始化点云）。
2.然后先将重心重合（平移），每个点以矩阵坐标上相等的点作为暂时的对应点。
3.进行旋转，使两个点云之间的距离平方和最小。
4.判断是否满足需求，不满足重复2，3步骤（迭代获取有意义的对应点）.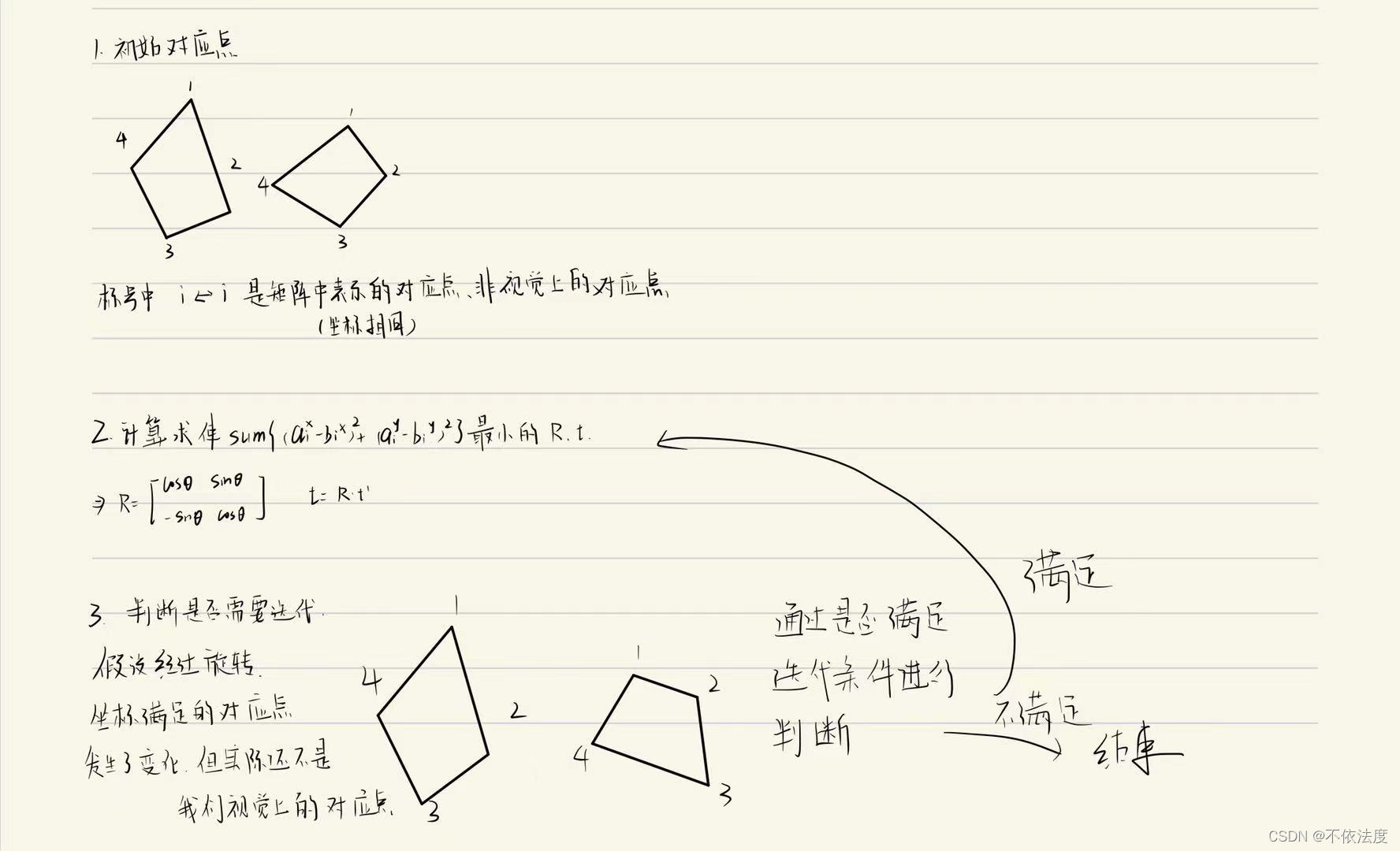
（我这图画的真丑…但是不碍事，能看就行）

ICP实现过程（匹配对应点）

输入

我们解析两张svg图片，得到svg图的所有关键点，为输入数据——两个点云（点集）。

初始化对应点

这里的a_i和b_j是视觉上（真正有意义）的对应点，需要迭代匹配才能得到。
{a_i,b_j}=arg min{sqrt( (a_i^x-b_j^x)² +(a_i^y-b_j^y)² ) },这是视觉上的对应点的定义，取距离最短的两点作为对应点。

迭代求旋转矩阵中用到的a_i，b_i是点云归一化后的对应点，不一定是视觉上的对应点
平移之后通过旋转确定点的匹配。
比如这张图，此时的a_i，b_i只是因为矩阵坐标上一致所以被认为是对应点。

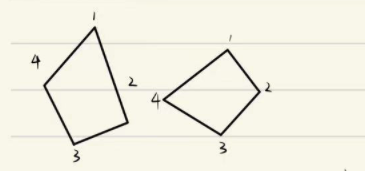
ICP算法最重要的就是找到对应的旋转和平移矩阵，使得变换后的两个点云近似匹配（对应点距离平方最小）

求旋转，平移矩阵

在对点云归一化的过程中，两个点云的重心已经重叠。已经实现部分的平移，所以我们接下来重心放在旋转上，得到旋转矩阵后就可以得到实际的平移矩阵 R*t^’。

t^’是点云归一化的矩阵——对于矩阵的每一个点-=点云重点。

关于迭代

第三点匹配失败是因为变化不大，没有迭代的必要了。
如果没有达到迭代终止的三种情况就继续迭代。

ICP代码

代码借鉴：这篇博客是基于三维图像进行的ICP算法的实现，我稍微改了一些东西
Eigen库的导入和使用参考1
Eigen库的导入和使用参考2
这段代码只是第一次旋转平移，初次尝试匹配，并加上迭代的功能。

#include <Eigen/Dense>
#include <iostream>
#include <string.h>
#include <fstream>
#include <vector>
#include<cmath>
using namespace std;
struct Point
{
	double x, y;
};

//功能：读取文件txt、asc->MatrixXd
void CreateCloudMatrix(const string& file_path, Eigen::MatrixXd& inPutPointCloud)
{
	ifstream file;
	file.open(file_path.c_str(), ios::in);
	if (!file.is_open()) {
		cout << "文件打开失败" << endl;
		exit(0);
	}

//	ifstream file();//c_str()：生成一个const char*指针，指向以空字符终止的数组。
	string line;
	Point point;
	vector<Point> cloud;
	while (getline(file, line))           //用到x，y,z
	{
		stringstream ss(line);
		ss >> point.x;
		ss >> point.y;
		cloud.push_back(point);
	}
	Eigen::MatrixXd pointCloud = Eigen::MatrixXd::Zero(cloud.size(), 2);//size行，两列
	for (int i = 0; i < cloud.size(); i++)
	{
		pointCloud(i, 0) = cloud[i].x;
		pointCloud(i, 1) = cloud[i].y;
	}
	inPutPointCloud = pointCloud;

	file.close();

}

//功能：SVD计算点集配准
//介绍：输入两个对应点云，输出旋转矩阵、平移矩阵。
void PointCloudRegistrationSVD(Eigen::MatrixXd inputPointCloud1, Eigen::MatrixXd inputPointCloud2, Eigen::Matrix2d& rotationMat, Eigen::Vector2d& translationMat)
{
	// MatrixXd 表示的是动态数组，初始化的时候指定数组的行数和列数
	//每列求均值->1X2
	Eigen::RowVector2d meanVector1 = inputPointCloud1.colwise().mean();  
	Eigen::RowVector2d meanVector2 = inputPointCloud2.colwise().mean();
	

	//平移后的矩阵
	//减去质心坐标，每行坐标减去上面的那个1X2矩阵
	inputPointCloud1.rowwise() -= meanVector1;                        
	inputPointCloud2.rowwise() -= meanVector2;	

	

	double sum1=0, sum2 = 0;
	for (int i = 0; i < inputPointCloud1.size()/2; i++) {
		sum1 += inputPointCloud1(i, 0) * inputPointCloud2(i, 1) - inputPointCloud1(i, 1) * inputPointCloud2(i, 0);
		sum2 += inputPointCloud1(i, 0) * inputPointCloud2(i, 0) + inputPointCloud1(i, 1) * inputPointCloud2(i, 0);
	}


	double Tan = tan(sum1 / sum2);
	double Atan = atan(Tan);
	

											  
	//点云1的所有坐标-=点云2的所有坐标*旋转矩阵（平移后的点云）
	rotationMat(0, 0) = cos(Atan);
	rotationMat(0, 1) = sin(Atan);
	rotationMat(1, 0) = -sin(Atan);
	rotationMat(1, 1) = cos(Atan);

	/*for (int i = 0; i < inputPointCloud1.size() / 2; i++) {
		cout << inputPointCloud1(i, 0) << " " << inputPointCloud1(i, 1) << endl;
	}
	cout << endl;
	for (int i = 0; i < inputPointCloud2.size() / 2; i++) {
		cout << inputPointCloud2(i, 0) << " " << inputPointCloud2(i, 1) << endl;
	}*/

	translationMat = meanVector2 - meanVector1 * rotationMat;

}

void test()
{
	Eigen::MatrixXd inPutPointCloud1;
	Eigen::MatrixXd inPutPointCloud2;

	Eigen::Matrix2d rotationMat;
	//旋转矩阵
	Eigen::Vector2d translationMat;
	//平移矩阵

	CreateCloudMatrix("C:\\Users\\mio\\Desktop\\data1.txt", inPutPointCloud1);
	CreateCloudMatrix("C:\\Users\\mio\\Desktop\\data2.txt", inPutPointCloud2);
	//初始化点云

	PointCloudRegistrationSVD(inPutPointCloud1, inPutPointCloud2, rotationMat, translationMat);

	cout << "旋转矩阵:" << endl;
	cout << rotationMat(0, 0) << " , " << rotationMat(0, 1) << endl;
	cout << rotationMat(1, 0) << " , " << rotationMat(1, 1) << endl;

	cout << endl << "矩阵1经过旋转矩阵后的变化:" << endl;
	for (int i = 0; i < inPutPointCloud2.size() / 2; i++) {
		
		cout << inPutPointCloud1(i, 0) * rotationMat(0, 0) + inPutPointCloud1(i, 1) * rotationMat(1, 0) << ","
			<< inPutPointCloud1(i, 0) * rotationMat(0, 1) + inPutPointCloud1(i, 1) * rotationMat(1, 1) << endl;
		
	}
	
}

int main()
{
	test();
}

对应点匹配成功后就可以确定两个svg图形是否满足相似性。

测试结果

测试了两个边长都是5的正方形。点存放顺序不一致的。
测试的时候发现一个问题，我的点必须连续存放，不能来回跳跃，不然匹配出的图像即使差不多可以重合。
匹配的对应点也不是我要的效果。

test1：

点顺序存储，对应点匹配成功

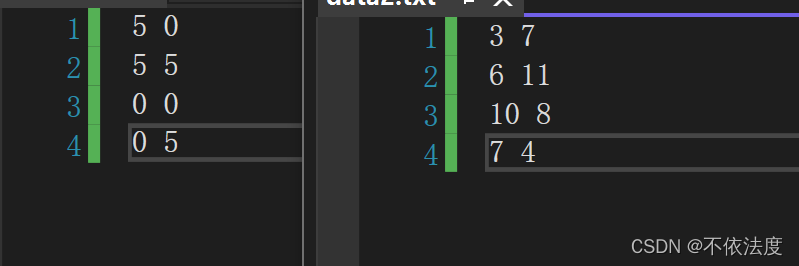
对应点

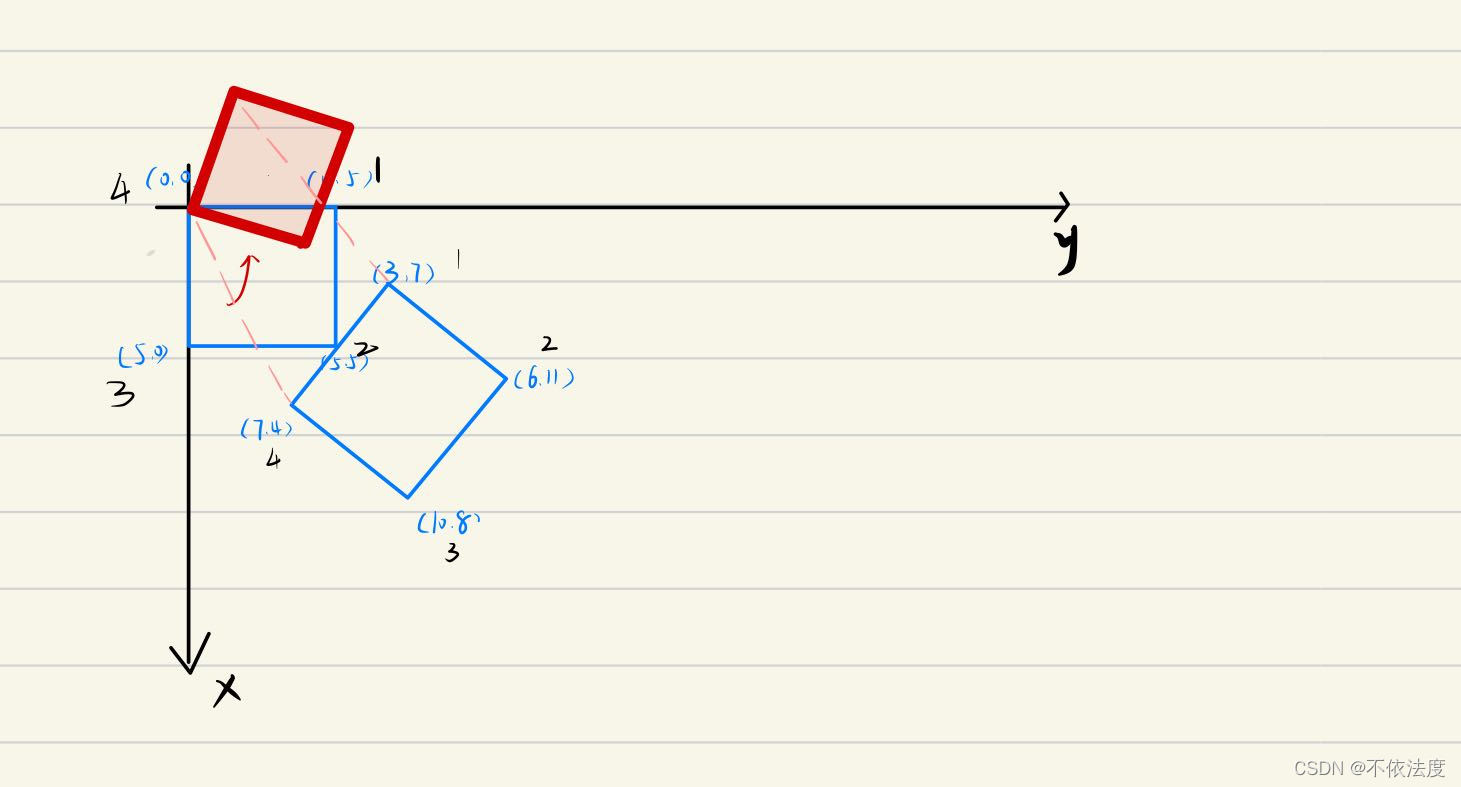
输出结果

test2：

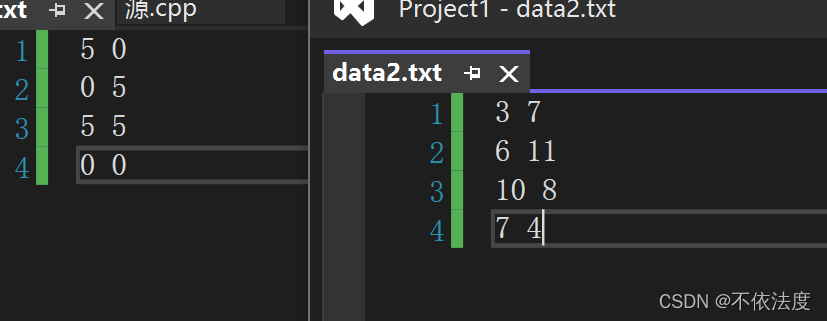
对应点
这个就是跳跃存储了1->2中间有3（逆时针
这样子匹配出来的图像上的对应点是
4-1
2-2
1-3
1-4
这种怎么迭代最后的对应点都不是真正意义上的对应点。

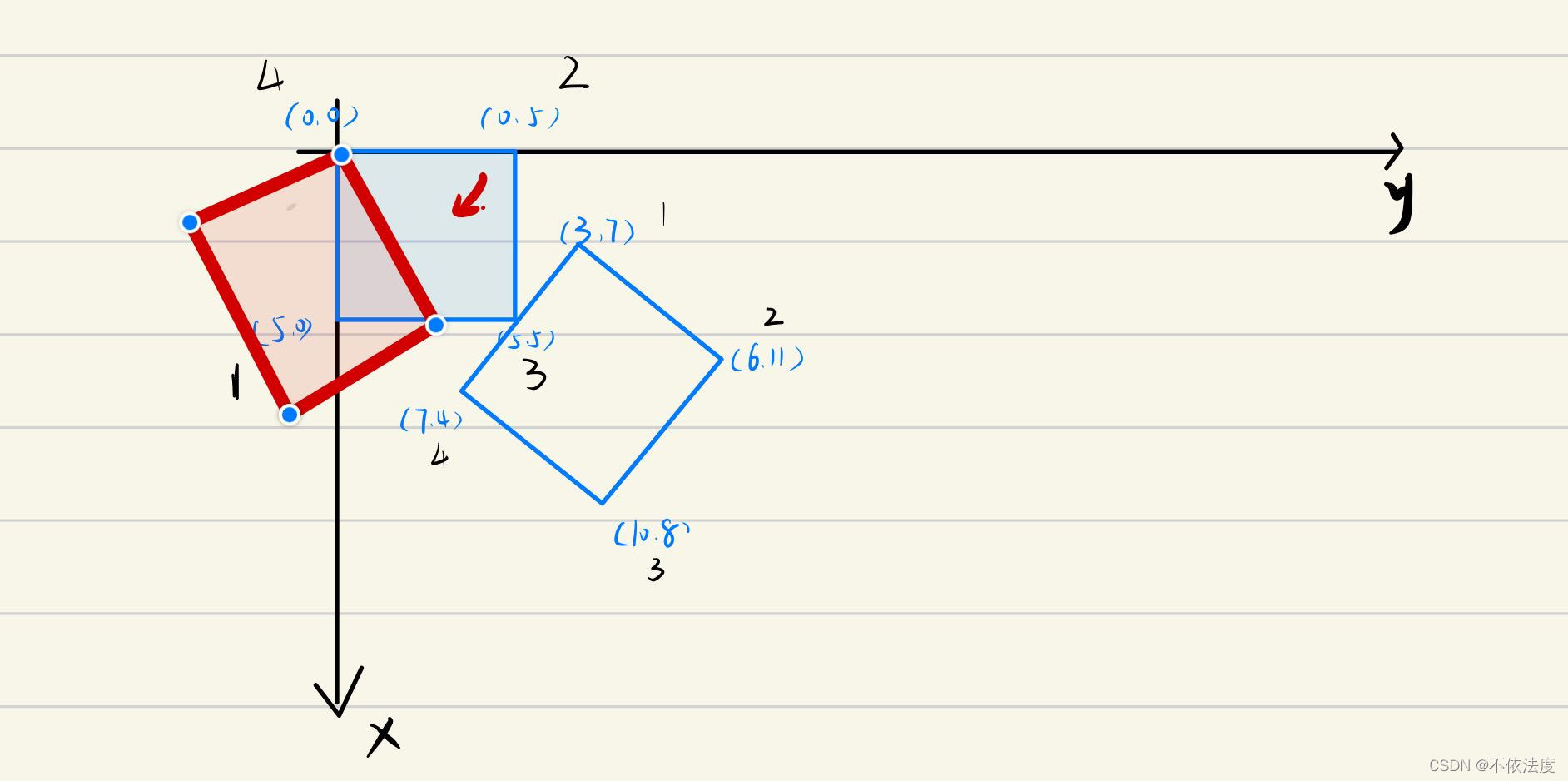
输出结果

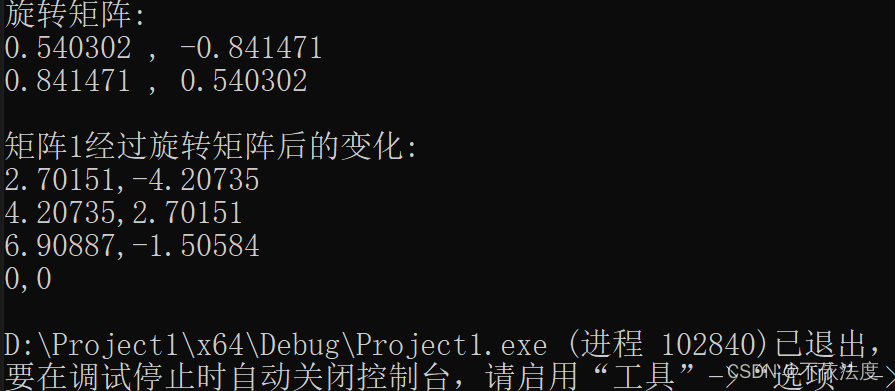
是否满足相似性