概述
这是一篇对稀疏卷积讲述非常全面的文章,理解起来毫不费事。这里要和SPConv相区别,这是两个完全不同的东西。SPConv是为了解决普通33卷积算子参数冗余而设计的,一种“即插即用”计算单元,可以随时随地替换普通33卷积算子,可以用来提高模型推理速度吧。跟剪枝算法差不多。
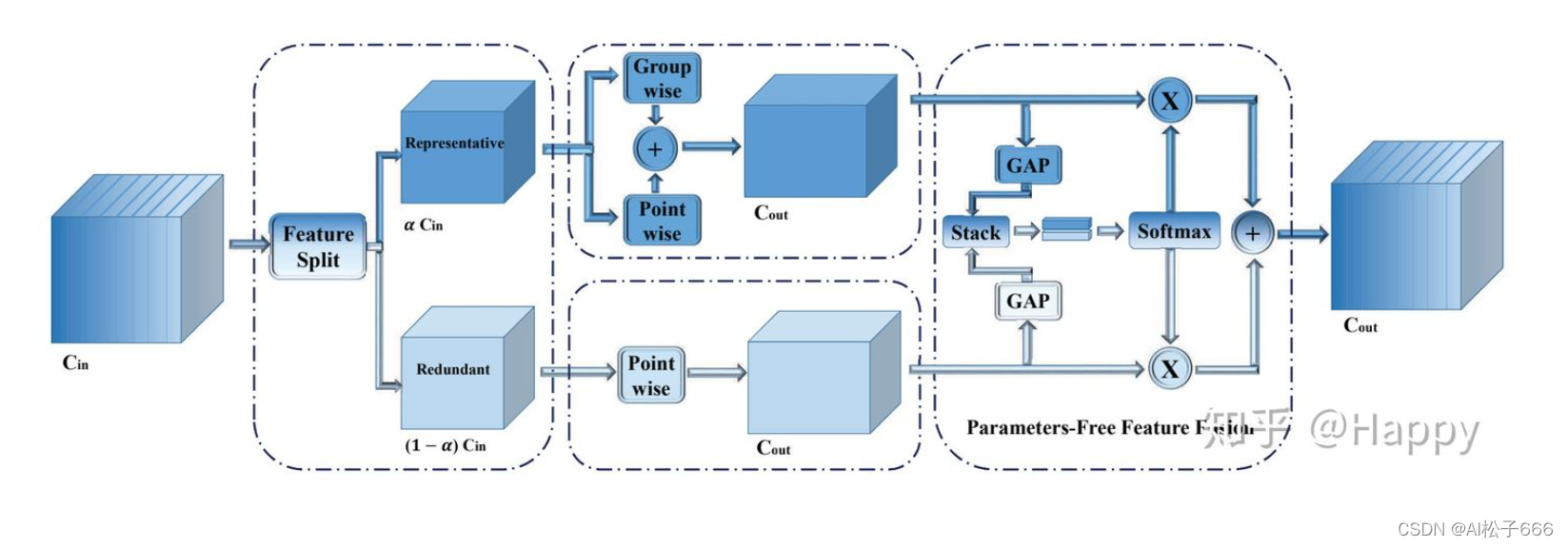
下面要讲述的是稀疏卷积Sparse Convolution Net,转载自https://zhuanlan.zhihu.com/p/383299678,写的十分详细。通俗易懂,方便读者理解。
简介
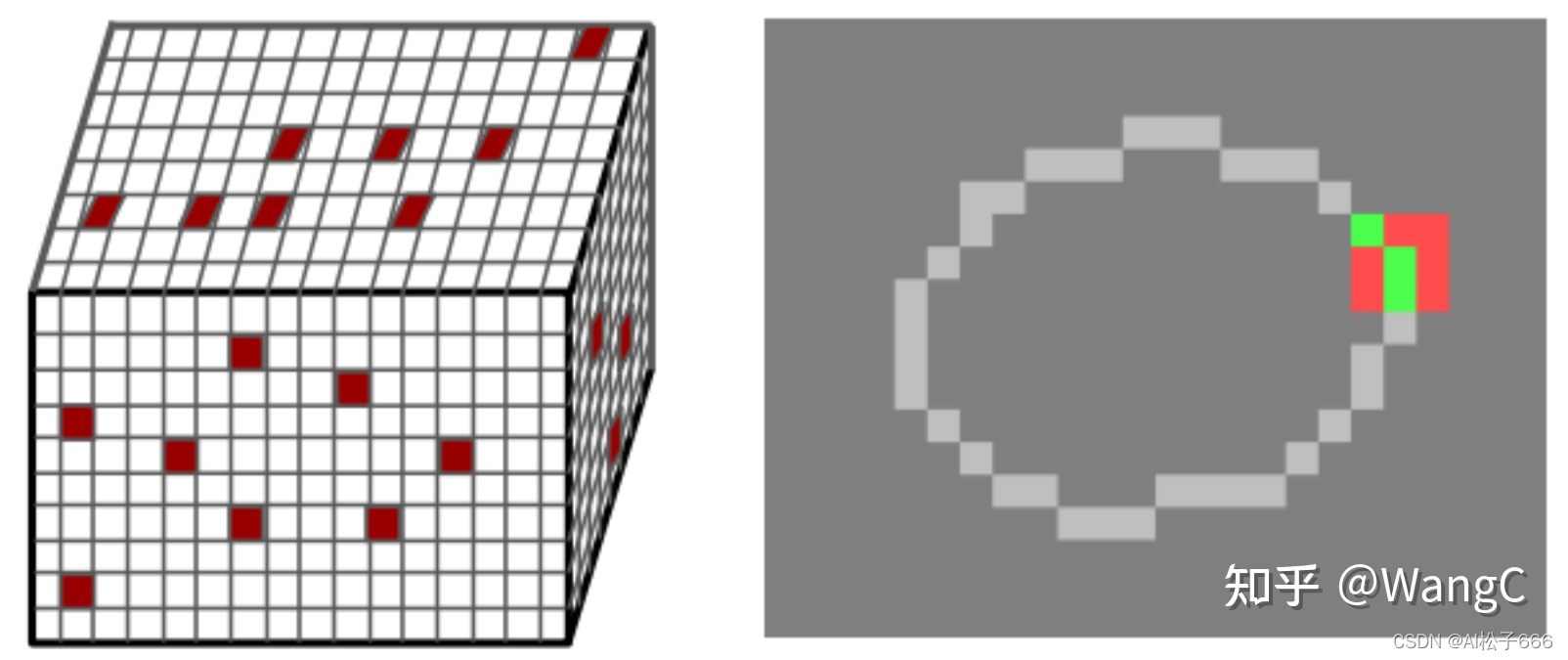
? 稀疏卷积常用于3D项目(如3D点云分割)中,由于点云数据是稀疏的,无法使用标准的卷积操作。同理,2D任务中,如果只处理其中一部分像素,也需要使用稀疏卷积,这样有助于模型加速。
原理解析
? 本质上就是通过建立哈希表,保存特定位置的计算结果。下文将通过举例说明稀疏卷积的原理。
输入数据
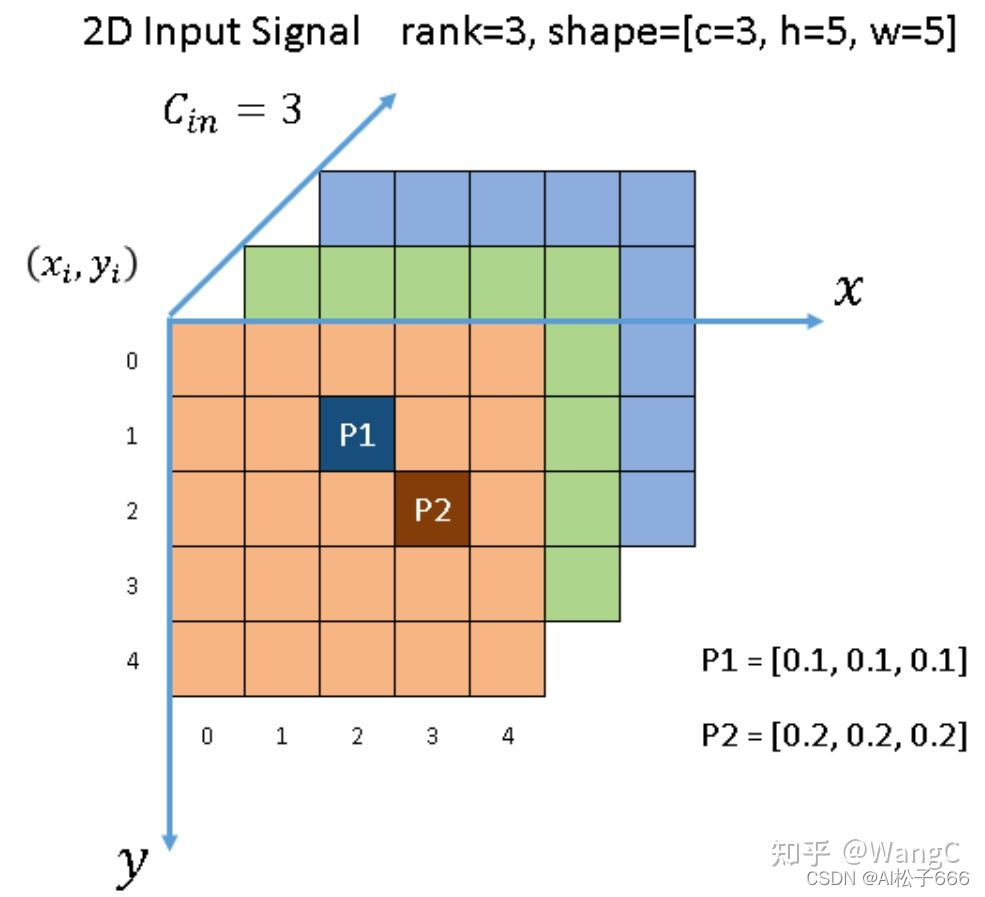
? 如下图所示,有一个3通道的 5x5 图像。除了两个点 P1 和 P2 之外,所有像素都是(0, 0, 0)。 根据 [1],P1 和 P2,此类非零元素(即P1、P2)也称为activate input sites。输入张量的形状按NCHW 顺序为[1x3x5x5]。在稀疏形式下,[P1,P2]数据列表为 [[0.1, 0.1, 0.1], [0.2, 0.2, 0.2]] ,索引列表为 [[1,2], [2, 3]] 。
卷积核
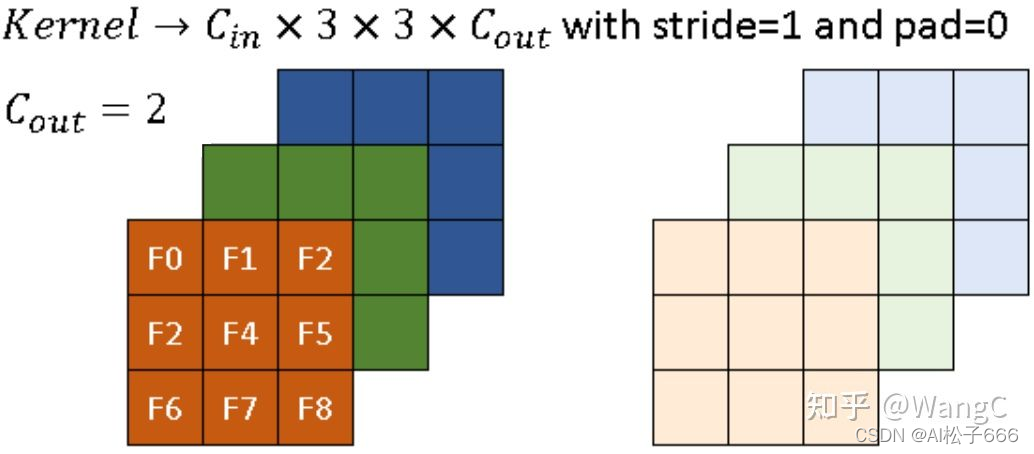
? 稀疏卷积的卷积核和传统卷积一样。下图是一个示例,其内核大小为 3x3。 深色和浅色分别代表 2 个卷积核。
输出定义
? 稀疏卷积的输出与传统卷积有很大不同。 稀疏卷积有两种输出定义[1]。 一种是regular output definition,就像普通卷积一样,只要核覆盖一个输入点就计算输出点。 另一种称为submanifold output definition。 只有当核中心覆盖输入站点时,才会计算卷积输出。
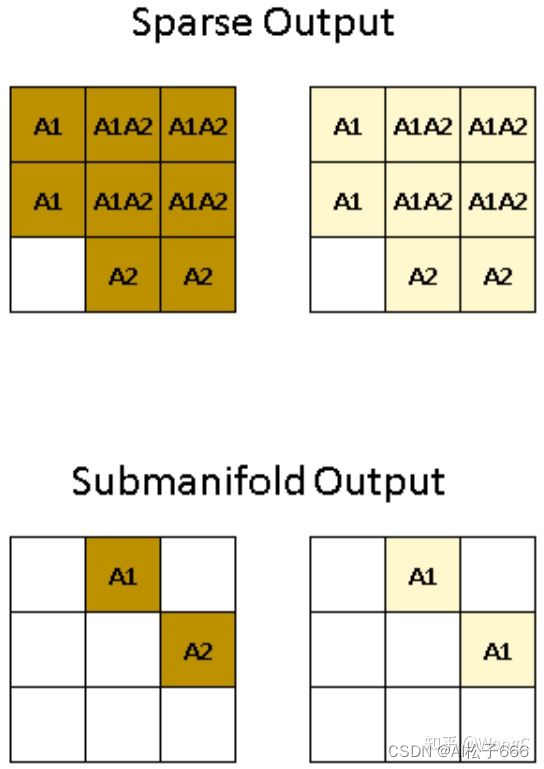
如上图所示, [公式] 输入图像, [公式] 卷积核,stride=1,padding=0,输出张量的尺寸为 [公式] 。第一行就是regular output definition,例如 (0,0)位置为A1,表示该位置的结果只与输入图像中的P1有关, (0,1) 位置为A1A2,表示该位置结果与P1、P2都有关。第二行是submanifold output definition,只有A1和A2有响应。不同的颜色要表示输出的不同通道。
计算实现
? 传统的卷积操作是通过 img2col 实现的,稀疏卷积[1]则通过Rulebook来实现计算。
建立哈希表
? 第一步,建立输入、输出张量的序号-坐标哈希表,以regular output definition输出为例。

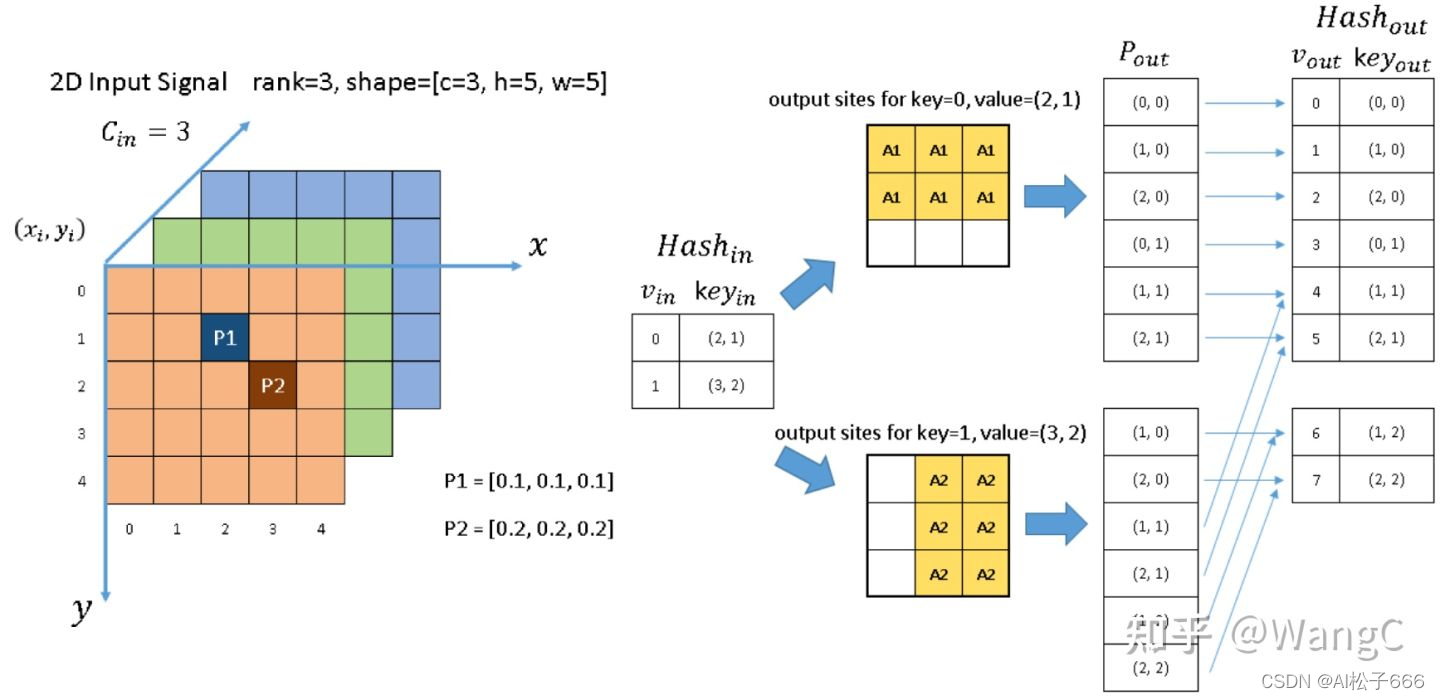
? 总结一下,这里哈希表的用处就是将张量坐标与序号一一对应,方便之后卷积计算好了值,将值放到张量的对应的位置。
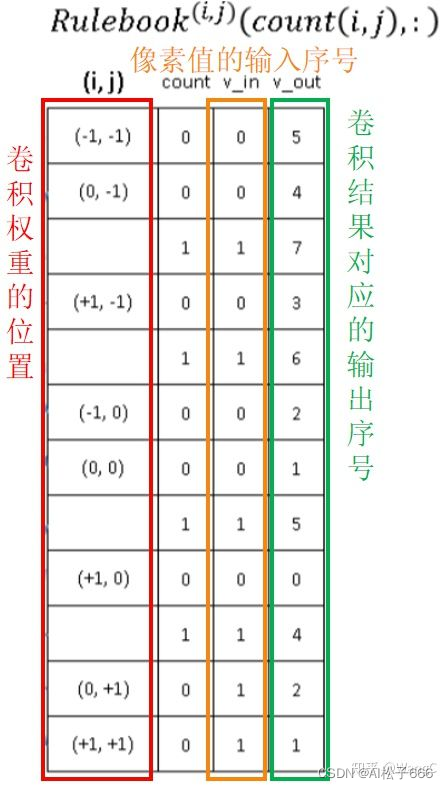
建立RuleBook
? 第二步,建立Rulebook。
? 什么是Rulebook? 本质上来说就是一个表。第一步我们建立输入、输出的哈希表,分别将输入、输出的张量坐标映射到序号。现在我们要将输入、输出的哈希表中的序号建立起联系,这样就可以基本实现了稀疏卷积,因此这也是稀疏卷积实现的关键。
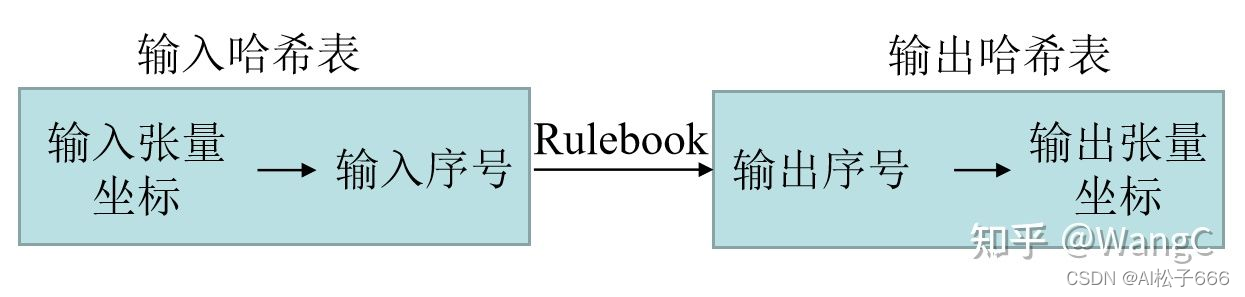
由上图可以Rulebook主要是实现输入序号到输出序号的映射。下图展示了如何构建Rulebook。
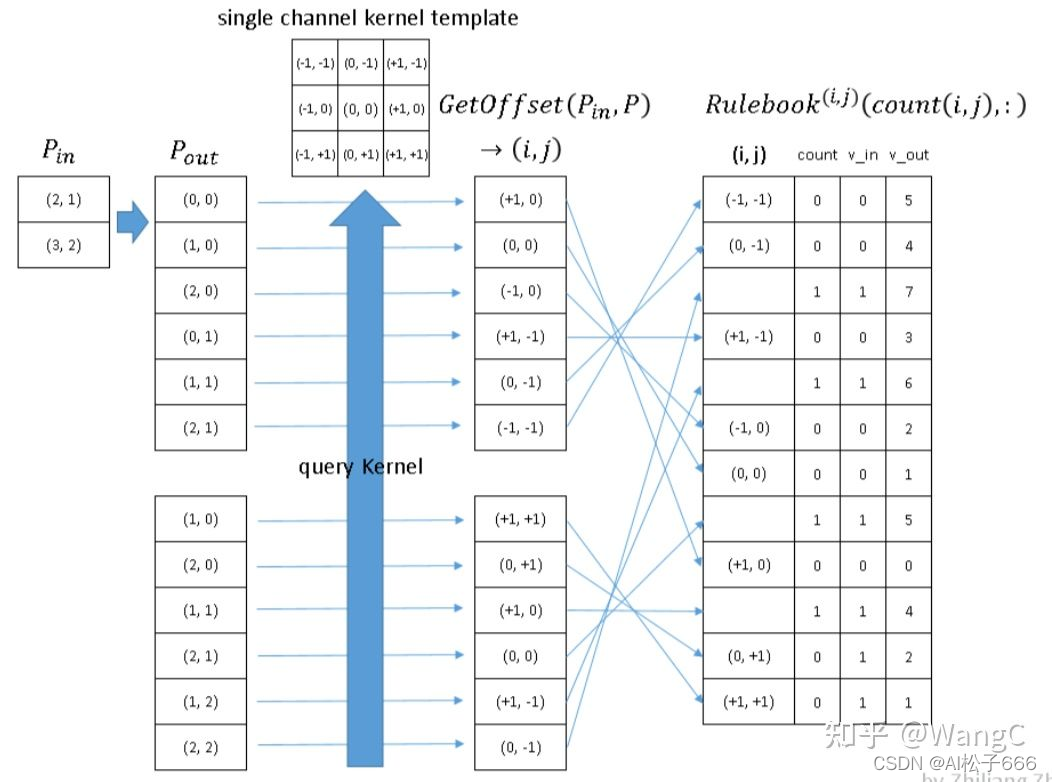

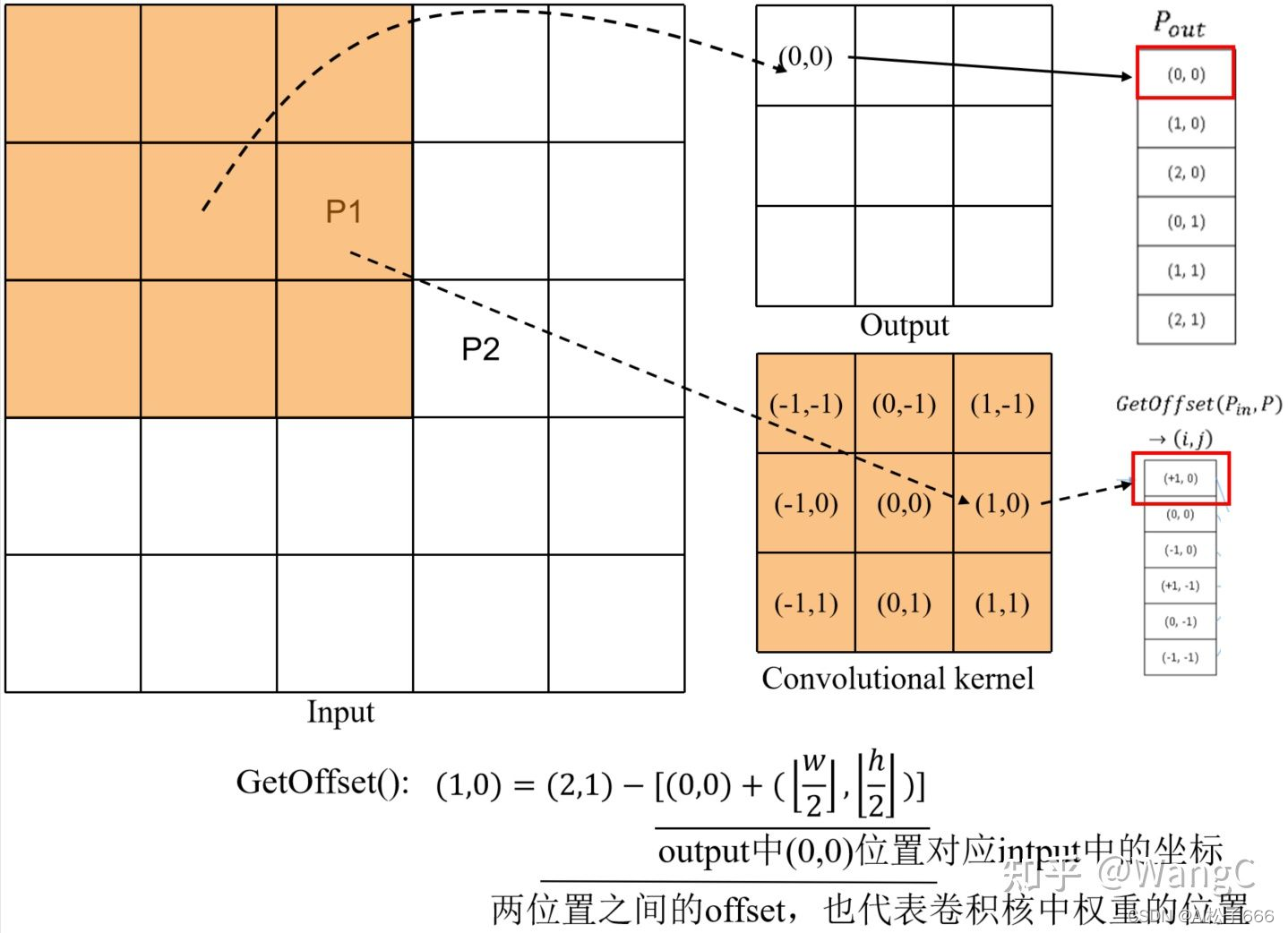
? 上面我们讲完了原理,那么每次都按上面原理推岂不是很麻烦,这里呢,我们推导了上面GetOffset()的公式。需要注意的是上面公式是在stride=1,padding=0的情况下的。
? 一句话来说,GetOffset()就是用于找出output中某位置需要用卷积核中的哪个weight来计算。
- 从GetOffset()到Rulebook
? 既然要完成卷积,上一步记录了卷积核权重的位置,那么这一步就需要记录对应的输入像素值,然后计算完了放哪里。如下图,我们可以看到Rulebook中红色方框为上一步记录的卷积核权重位置,橙色方框为输入像素值的输入序号,绿色方框为卷积结果对应的输出序号。
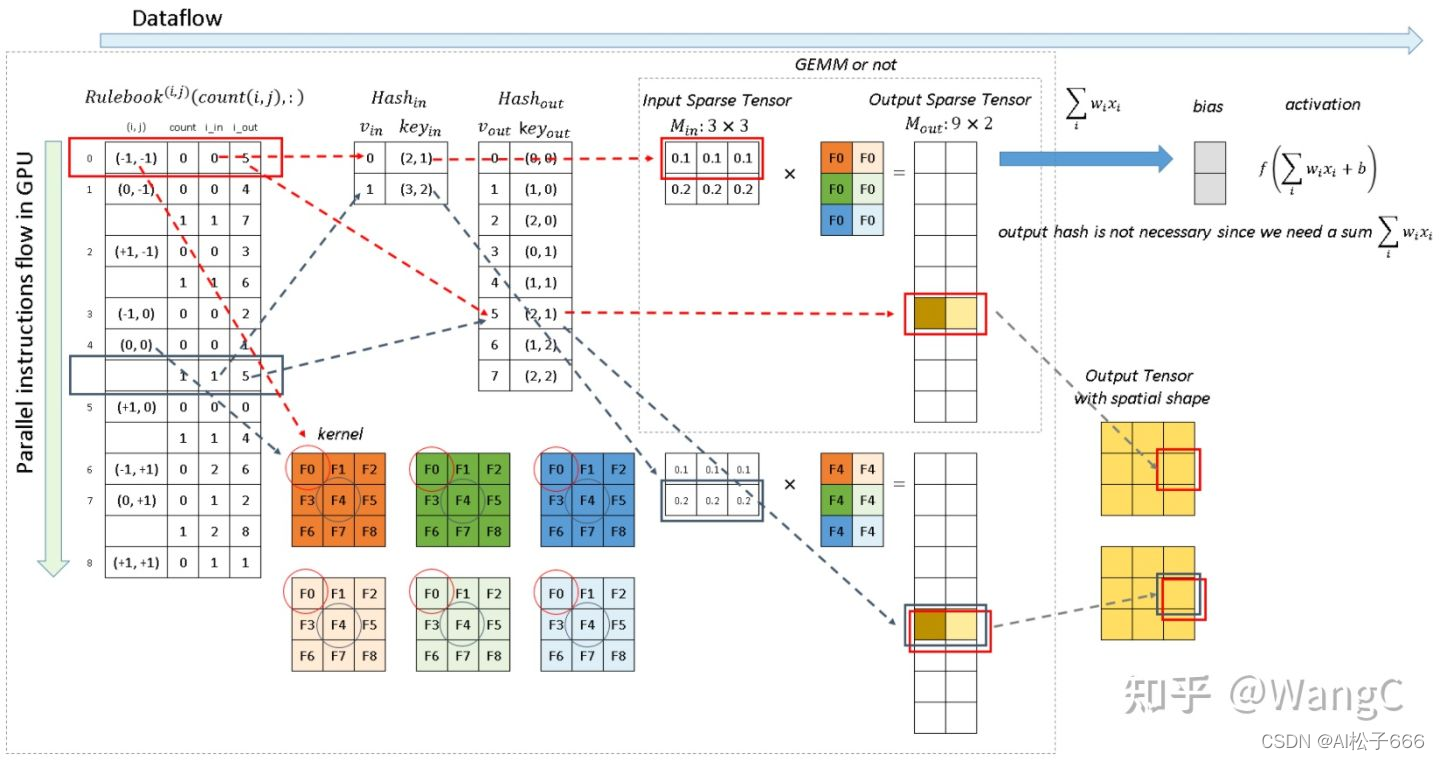
稀疏卷积的GPU实现
? 稀疏卷积实现时是通过查询Rulebook,因为可以通过GPU并行实现,因此效率比较高。

总结
以上就是Sparse Convolution Net的实现原理,主要就是通过数据结构——表来实现。在实际使用时通常不需要大家自己重新写一个卷积的底层操作,目前Facebook已经有开源的稀疏卷积库,关于稀疏卷积的使用见一篇文档。
https://link.zhihu.com/?target=https%3A//github.com/facebookresearch/SparseConvNet