[人工智能]【多模态论文阅读】Multi-modal Factorized Bilinear Pooling with Co-Attention Learning for Visual Question Ans

一、亮点

1. 对于多模态特征融合，本文开发了一种多模态因子双线性（MFB）池化方法来有效地组合多模态特征；
2. 对于细粒度的图像和问题表示，开发了一种“共同注意”机制，使用端到端的深度网络架构来共同学习图像和问题的注意力。

二、MCB和MLB的缺点

MCB 模型依赖于高维输出特征来保证稳健的性能，这可能会由于巨大的内存使用量而限制其适用性。 为了克服这个问题，Kim 等人提出了基于两个特征向量的Hadamard乘积的多模态低秩双线性化（MLB）池模型。 由于 MLB 生成的输出特征维度较低，模型参数较少，因此与 MCB 具有很强的竞争力。 然而，MLB 的收敛速度较慢，并且对学习的超参数很敏感。 为了解决这些问题，本文开发了多模态分解双线性池（MFB）方法，该方法具有 MLB 的紧凑输出特征和 MCB 的强大表达能力的双重优点。

三、模型结构

3.1 MFB

最简单的bilinear model定义如下：

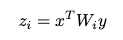
然后引入矩阵分解，得到：

上面只是输出向量的一个值，为了得到o维输出向量，则需要o个Ui和Vi，即：

通过reshape可以将U和V张量转换为矩阵，即：

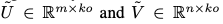
于是，z的表达式可以被写为：

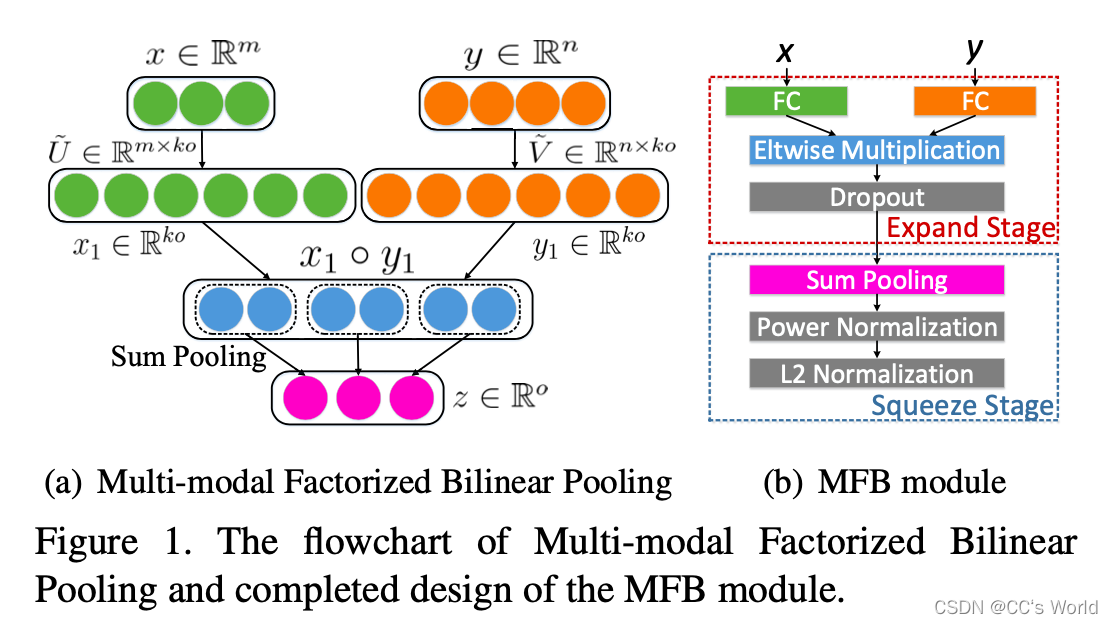
其中函数SumPooling(x，k)意味着使用大小为k的一维非重叠窗口对x执行SumPooling。该方法可以通过组合一些常用的层来容易地实现，例如完全连接层、按元素的乘法和汇集层。此外，为了防止过度拟合，在元素方向倍增层之后添加了Dropout层。由于引入了逐元素乘法，输出神经元的大小可能会有很大的变化，模型可能会收敛到一个不令人满意的局部最小值。所以引入了power归一化。

3.2 Relationship to MLB

MLB 是所提出的 MFB 的一个特例，其中 k = 1，对应于 rank-1 分解。 形象地说，MFB 可以分解为两个阶段（见图 1（b））：首先，将来自不同模态的特征扩展到高维空间，然后与元素乘法相结合。 之后，进行归一化层后的 sum pooling 将高维特征压缩到紧凑的输出特征中，而 MLB 直接将特征投影到低维输出空间并执行逐元素乘法。 因此，在输出特征维数相同的情况下，MFB 的表示能力比 MLB 更强大。

3.3 MFB with Co-Attention

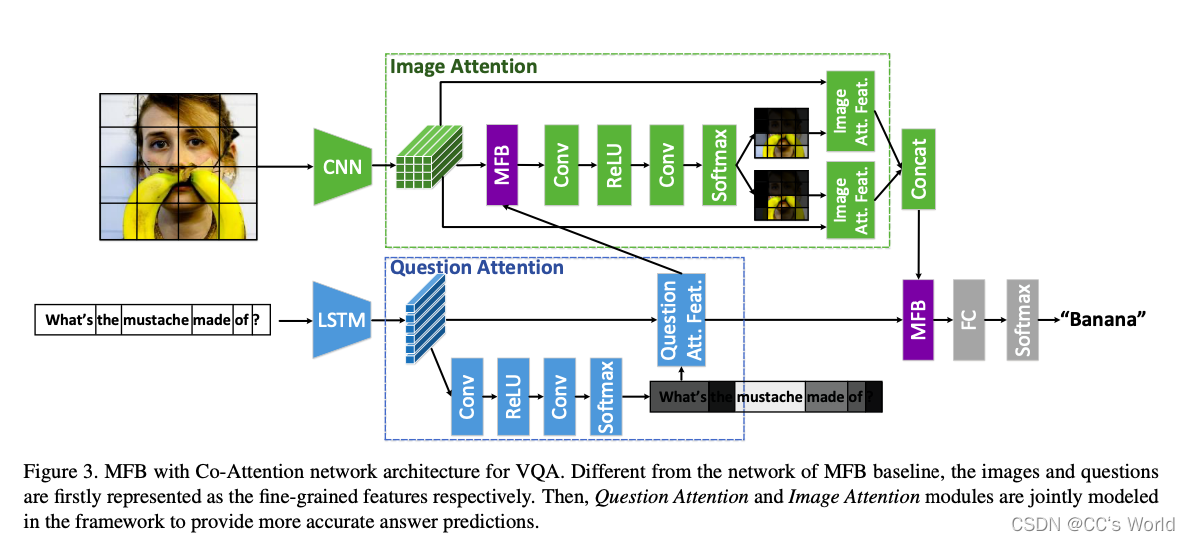
图像和文本模块是松散耦合的，因此我们在学习文本注意模块时不会利用图像特征。 这是基于人的基本认知，因为我们假设网络可以直接推断问题注意力（即问题的关键词），而无需看到图像。

参考资料

1. Multi-modal Factorized Bilinear Pooling with Co-Attention Learning for Visual Question Answering论文笔记
2. 《Multi-modal Factorized Bilinear Pooling with Co-Attention Learning for VQA》论文笔记