1.KS检验
Kolmogorov–Smirnov 检验,简称KS检验,是统计学中的一种非参数假设检验,用来检测单样本是否服从某一分布,或者两样本是否服从相同分布。当p值>=0.5时,可认为数据符合对应检验的分布。
下面以检验正态分布为例
from scipy.stats import kstest
import numpy as np
import pandas as pd
np.random.seed(10)
n = np.random.randn(10000)
n = pd.DataFrame(n)
p = kstest(n[0], "norm", N=len(n))
print(p)

p>=0.05说明数据符合正态分布
2.幂律分布检验
符合y = c * x ^ (-r)的数据分布为幂律分布,是一种比较特殊的分布,且在我们的生活时常出现,我这里的检验思路就是两边各自取对数转换成lny = lnc - rlnx,然后进行线性拟合,如果拟合效果较好,可以说明此数据符合幂律分布。
# coding:utf-8
from sklearn import linear_model
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib as mpl
from scipy.stats import kstest
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定中文字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
f = pd.read_csv("文件名.tsv", sep="\t", encoding="utf-8", low_memory=False)
col = "待检验的数据列名"
d = f[(~f[col].isnull())][col]
data = d.value_counts(normalize=True) # 计算出现概率
data = pd.DataFrame([list(data.index), list(data)]).T
data.columns = ["x", "y"]
data["x"] = np.log(data["x"]) # 对数转换
data["y"] = np.log(data["y"])
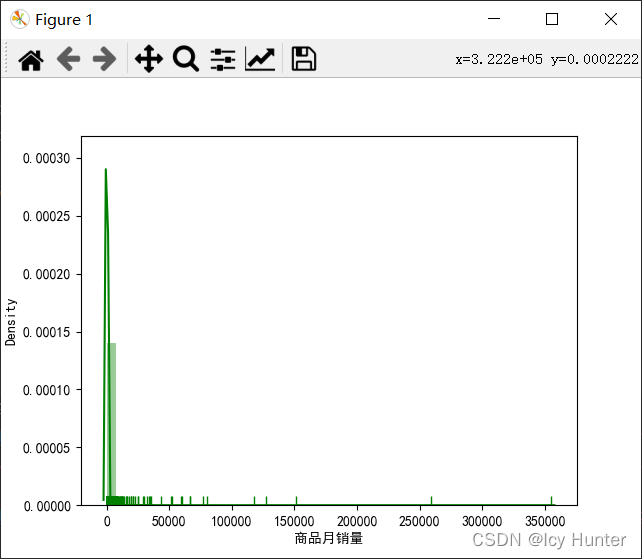
sns.distplot(f[(~f[col].isnull())][col], rug=True, hist=True, kde=True, color="g") # 粗略看一下数据分布图
plt.show()
reg = linear_model.LinearRegression() # 线性拟合
reg.fit(np.array(data["x"]).reshape(-1, 1), np.array(data["y"]))
pre = reg.predict(np.array(data["x"]).reshape(-1, 1))
data["pre"] = pd.DataFrame(pre)
fig = plt.figure(figsize=(15, 8), dpi=80)
ax1 = fig.add_subplot(111)
ax1.scatter(data["x"], data["y"])
ax2 = ax1.twiny()
ax2.plot(data["x"], data["pre"], color="r")
plt.show()
print(reg.coef_) # 求出的-r
print(reg.intercept_) # 求出的lnc
print(reg.score(np.array(data["x"]).reshape(-1, 1) # 计算R平方,检验拟合效果
np.array(data["y"])))
# 检验正太分布
p = kstest(f[col], "norm", N=len(f[col]))
print(p)
下面展示我的结果
数据分布粗略图,看起来有点像幂律分布
对数转换后的散点图和拟合直线的图,看得出散点确实挺像一条直线的
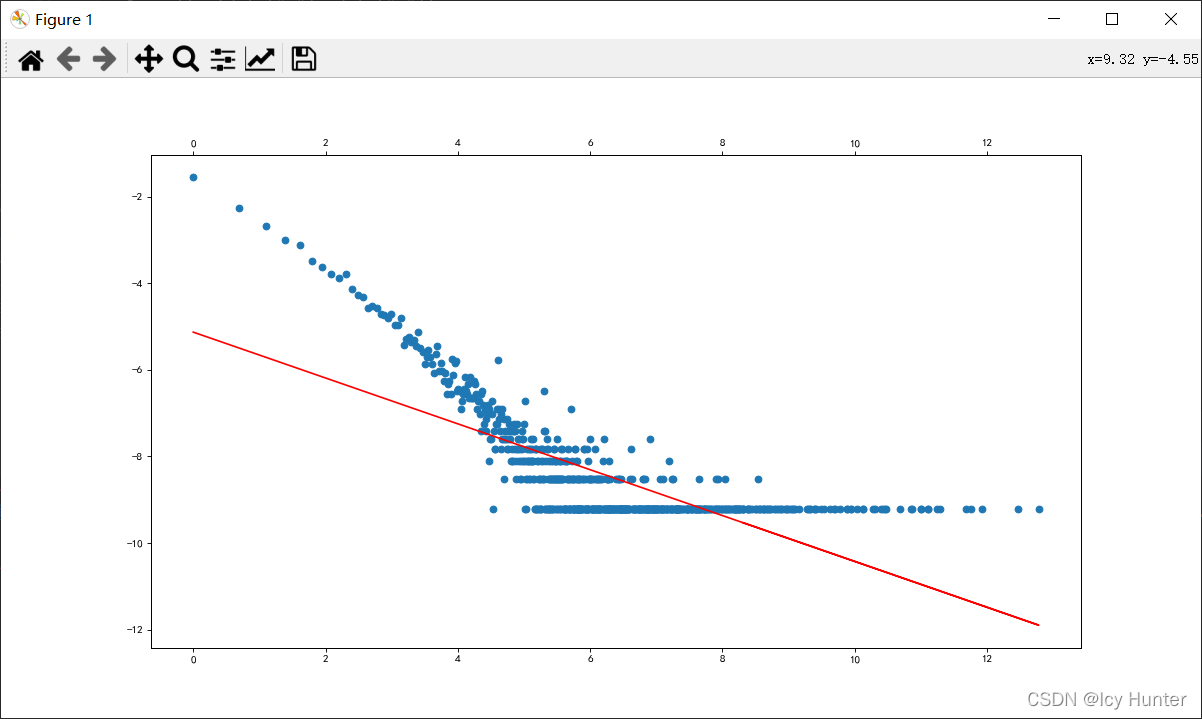

R^2 = 0.5495, 怎么说呢,说明拟合效果是有一点的吧
下面的正态分布检验p=0.0说明数据不符合正态分布
因此,目前看来,认为这组数据为幂律分布。