贝叶斯
贝叶斯分类算法是统计学的一种分类方法, 它是一类利用概率统计知识进行分类的算法。
贝叶斯定理由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展,用来描述两个条件概率之间的关系,比如 P(A|B) 和 P(B|A)。
按照乘法法则,可以立刻导出:P(A∩B) = P(A)*P(B|A)=P(B)*P(A|B)。
如上公式也可变形为:P(A|B)=P(B|A)*P(A)/P(B)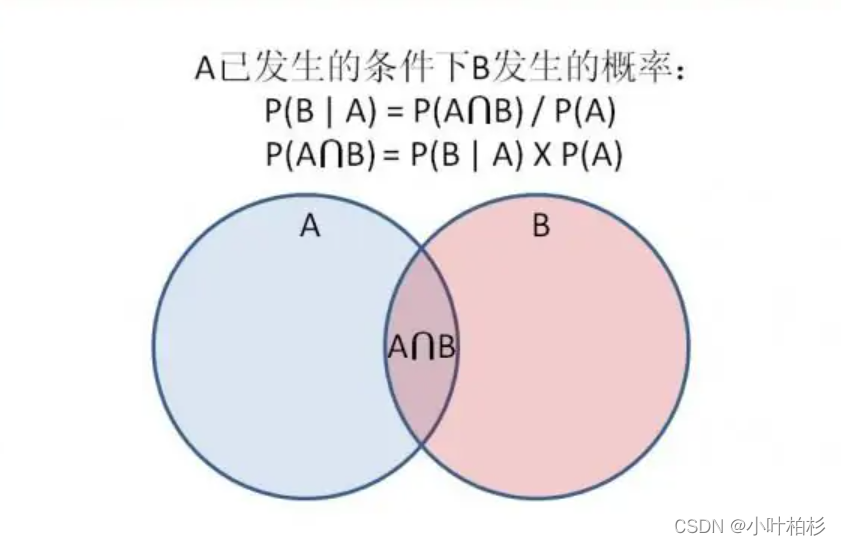
贝叶斯公式
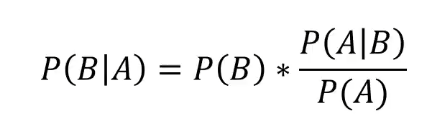
公式的延伸:
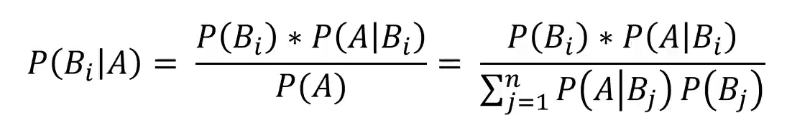
概率是反映随机事件出现的可能性大小的量度,而条件概率则是给定某事件A的条件下,另一事件B发生的概率。 全概率公式则是利用条件概率,将复杂事件A分割为若干简单事件概率的求和问题。贝叶斯公式则是利用条件概率和全概率公式计算后验概率。
全概率公式
将复杂事件A的概率求解问题,转化为在不同情况下发生的简单事件的概率的求和问题,公式为:
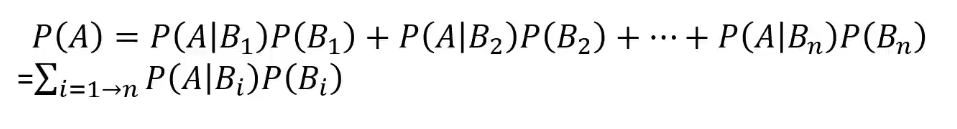
朴素贝叶斯
朴素贝叶斯法是基于贝叶斯定理 与特征条件独立假设的分类方法。最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model, NBM)。
在许多场合,朴素贝叶斯(Naive Bayes, NB) 分类算法可以与决策树和神经网络分类算法相媲美,该算法能运用到大型数据库中,而且方法简单、分类准确率高、速度快。
朴素贝叶斯算法公式
以贝叶斯定理为基础) [假设特征之间相互独立,先通过训练数据集,学习从输入到输出的概率分布,再基于学习到的模型及输入,求出使得后验概率最大的输出实现分类。
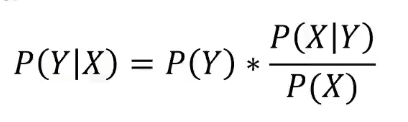
特征之间相互独立:
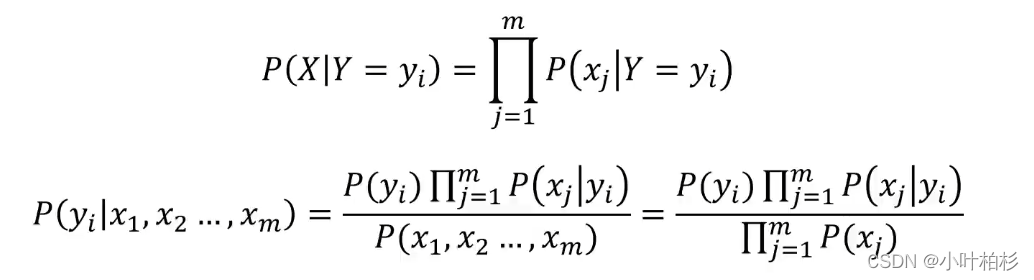
算法另一种讲解
朴素贝叶斯分类器基于一个简单的假定:给定目标值时属性之间相互条件独立。
贝叶斯公式:

朴素贝叶斯:
将一个完成
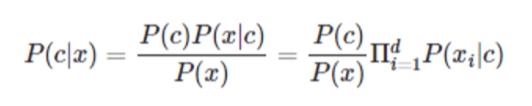
朴素贝叶斯 比 贝叶斯 概率准确性高
朴素贝叶斯算法应用场景
常用场景
-
文本分类:
正面信息有多少,负面信息有多少。还可以对文章分类,做成一个分类器。
例如:涉政文章,涉黄文章,广告文章,诈骗文章,其他垃圾文章等。 -
垃圾邮件过滤
把垃圾邮件过滤掉,例如开票,广告,违法等邮件。 -
多分类实时预测
传入文本,图像,音频,立即做出回应,区分是否违规,返回给用户。 -
拼写纠错
写文章,编辑,WORD时,打出标记红线,黄线,判断是否存在语法问题。
示例:
要把以下内容的垃圾文件过滤,可能是文本,图片
我司可代开普通增值税发票,税点优惠,欢迎来电咨询。
处理步骤:
- 进行分词
- 根据每个词出现的概率,求出正常邮件的概率,以及垃圾邮件的概率。
- 再进行对比,正常词占的百分比多,还是垃圾的词占的百分比多。
- 得出结果,这是垃圾邮件还是正常邮件。
C=P(“我”|S)P(“司”|S)P(“可”|S)P(“代开”|S)P(“普通”|S)P(“增值税”|S)P(“发票”|S)P( “税点”|S)P(“优惠”|S)P(“欢迎”|S)P(“来电”|S)P( “咨询”|S)P(“垃圾邮件”)
根据朴素贝叶斯算法,先求出每个分词占垃圾邮件的概率是多少,再累加相乘,得到一个总体概率。例如最后得出0.3 有30%的概率是垃圾邮件。
在计算出正常邮件的概率
W=P(“我”|H)P(“司”|H)P(“可”|H)P(“代开”|H)P(“普通”|H)*P(“增值税”|H)P( “发票”|H)P( “税点”|H)P( “优惠”|H)P( “欢迎”|H)P( “来电”|H)P(“咨询”|H)P(“正常邮件”)
得出概率:0.05
给出这个邮件是个垃圾邮件。