[人工智能]深度深度网络设计中各种归一化方法总结

前言

狭义的归一化指对输入特征进行归一化， 这在经典的机器学习中用的比较多，目的是为了消除不同特征量纲的差异。常用的归一化方法包括： Z-score, Min-Max scaler等等。

这里，我们主要总结深度学习中的一些归一化的技巧。深度学习中的归一化已经不仅仅局限于输入数据的归一化，而是网络各个层的归一化，因为每个层相当于一个非线性变换， 随着网络层数的加深，数据分布会发生较大变化（即internal covariate shift）。归一化实际上起到正则化的作用，能够大大促进网络的训练和收敛， 减轻了对参数处置的敏感性， 允许模型以更大的学习率进行训练。

批量归一化 BN

Batch Normalization顾名思义就是对每个min-batch samples进行归一化，

下图为一个BN变换的伪码， 其中$m$为Batchsize的大小，$x_i$实际上就是就是第i个样本feed forward到某个层的某个神经元节点的input(也就是上一层的输出的加权和)
可以看到：
1.BN操作实在Batch维度上进行的，具体：每个Batch包含m个样本，基于这m个samples为每个feature独立计算均值和方差，然后进行类似于Z-Score的操作，最后通过trainable parameters进行伸缩和平移，目的是为了保证BN变换为恒等变换。

实际上BN操作可以看作一个独立的网络层。

下面是BN变换更加抽象的一种写法，增益参数$g_i^l$, 这里的$a_i^l$表示第l层的第i个节点的输入，它实际上就是由上一层输出$h_l$经过Linear projection得到:

那么在网络训练和推断的过程中如何使用BN呢?
以前是每层的输入$x$直接作为该层的Input，有了BN以后，x首先用于计算BN的输出$y$,然后再把y作为该层Input, 这样以来，网络修改完毕 （见下图伪码2-5）。

网络修改完成后就可以再进行训练以同时优化原始模型参数和BN操作的参数($\lambda ,\beta$)了。

训练完成后，就可以将其用于推断了，这里的问题是： 推断时Batch=1, 如何来估计均值和方差呢？
这里使用所有mini-batches的samples来估计均值和方差,其在整个Inference的整个过程中是保持不变的，具体：
$E[x]\leftarrow E_B[{\mu }_B]$
$Var[x]\leftarrow \frac{m}{m?1}{E}_B[{\sigma }_B^2]$

这样以来，对于测试样本$x$， 它的normalized input可以估计为：
$\hat{x}=\frac{x?E[x]}{\sqrt{Var[x]+?}}$

相应的BN变换可以写为：
$y=\lambda \hat{x}+\beta =\frac{\lambda }{\sqrt{var[x]+?}}x+(\beta ?\frac{\lambda E[x]}{\sqrt{var[x]+?}})$

BN如何应用到卷积网络中呢？
原文中有这样的表述： we let B be the set of
all values in a feature map across both the elements of a
mini-batch and spatial locations，可见对于一个尺寸为(B, C, H，W)的Tensor, B,H,W这三个维度是共享归一化参数的，换句话说，BN操作逐Channel独立进行的，更严格的数学定义如下：


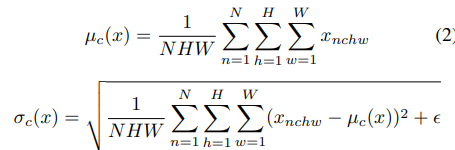
归一化参数($\mu ,\sigma$)总共有2C个。

缺点：
1.Batchsize的设置对BN的效果有很大影响；
2.BN主要是应用的前馈神经网络，尚不清楚如何用到循环网络中(RNN是按timestep展开的深度神经网络，假定RNN中使用BN的话，需要为每个timestep存储相关的统计信息，如果test sequence的长度比training sequence的长度还长，这显然会出问题)；

层归一化LN

Layer Normlaization 顾名思义就是对每个Layer内各个神经元的输入进行归一化，换句话说，Leyer内的各个神经元共享归一化参数，并且这些参数与Batchsize的大小无关，从而克服了BN中对BatchSize的依赖，可以用到Online Scenario (例如RNNs)。

上述参数的计算如下，H为某隐层的神经元节点的数量，

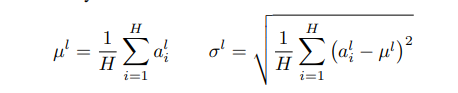
对于RNN, LN的定义如下， 其中$g$和$b$分别代表增益参数和偏置参数：

其中第$t$步的输入$a^t$计算如下：

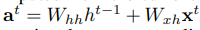
众所周知，标准的RNN极易出现梯度爆炸和梯度消失的问题，加入了LN以后，LN使得对某一层所有的Summed inputs的缩放不会引起average summed input产生变化，这使得隐藏层之间的动态变化、信息流更加稳定；

LN是在RNN背景下提出的，也可以将其应用到全连接前馈神经网络(FFNN)中, 具体上面公式中的H表示隐层节点的数量， 那么如何将其用到卷积网络CNN中呢？

由于每个卷积核用于从Input中提取某种Pattern,因此对于一个尺寸为（B,C, H,W）的Tensor, LN实际上是在C， H, W三个维度上进行的，其数学定义如下：
$LN(x)=\lambda (\frac{x?\mu (x)}{\sigma (x)})+\beta$
${\mu }_b(x)=\frac{1}{HWC}{\sum }_{h=1}^H{\sum }_{w=1}^W{\sum }_{c=1}^C{x}_{bchw}$
${\sigma }_b(x)=\sqrt{\frac{1}{HWC}{\sum }_{h=1}^H{\sum }_{w=1}^W{\sum }_{c=1}^C(x_{bchw}?{\mu }_b(x){)}^2+?}$
LN的归一化参数量为2B。

实例归一化IN

Instance normalization (IN), 顾名思义是在Instance level进行归一化， 实际上它与BN的区别也在于此： BN是在整个samples上进行归一化，Batch维度共享归一化参数，而IN是在逐个Sample内进行归一化。 其数学定义如下：

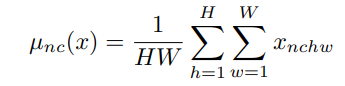
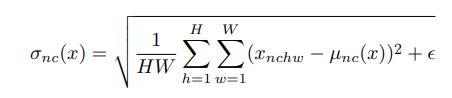
对于尺寸为（B,C, H,W）的Tensor, 总的归一化参数($\mu ,\sigma$)的数量为：2BC (而BN只有2C个).。

提到IN, 有必要提及著名的自适应实例归一化（Adaptive Instance Normalization, AdaIN）, AdaIN在很多经典的Style transfer的研究中都有使用。 什么是AdaIN？
AdaIN基于所谓的Conditioned Instance Normalization (CIN)进一步发展而来，主要作用是直接使用Target style的统计信息（对应$\lambda ,\beta$）来对Normalized Content image的style进行迁移，其数学与IN操作非常类似，定义如下：

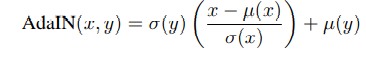
可以看到，括号里面是对Input image进行Normalize操作， 在IN中，$\lambda ,\beta$分别对应scale和shift的参数， 也是网络需要去学习的参数。而在AdaIN里面，对应的参数$\sigma ,\mu )$表示的是任意Style Image的统计信息， 不需要通过训练获得。简而言之， AdaIN通过在Feature spapce 迁移Feature statistics进行Style Transfer，

组归一化GN

Group Normalization (GN)与Layer Normalization之间的关系就像分组卷积相比于常规卷积。简单来说，就是把Chanel维度分为G（G为预定义的超参数）个组， 然后组内独立进行Layer Normalization。 对于尺寸为（B,C,H,W）的Tensor, GN的归一化参数($\mu ,\sigma$)的数量为2BG （是LN归一化参数的G倍)。

局部响应归一化LRN

Local Response Normalization (LRN)最早在AlexNet中被提出， 与上面几种归一化技术不太一样，LRN实际上仿造了生物学上活跃的神经元对相邻神经元的抑制现象（侧抑制），其数学定义如下：

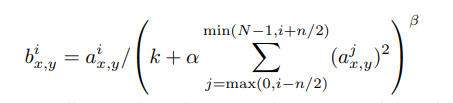
其中$a_{x,y}^j$表示将第j个Kernel应用到位置(x,y)后的非线性激活值，$b_{x,y}^j$即为其对应的LRN后的值。

可以看到LRN实际上就是在Channel方向上进行局部响应归一化， 具体来说：对于第i个channel的任意位置，基于其前n/2和后n/2对应位置的信息进行局部归一化，示意图如下：

总结->各种归一化的统一数学表达形式

如上图，不同的归一化方式的区别仅在于共享归一化参数的维度不同，具体来说：
BN是逐Channel进行的，
LN是逐Sample进行的
IN 逐Channel， 逐Sample进行的
GN是逐Sample， 且Channel维度逐Group进行的

上面4中归一化的统一数学表达形式为 (此处忽略Scale和Shift操作)：


区别就在于集合$S_i$的定义上， 具体：
BN中，

LN中，

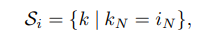
IN中，

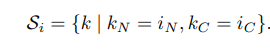
GN中，

Ok.

References

1. ImageNet Classification with Deep ConvolutionalNeural Networks;
2. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift;
3. Layer Normalization;
4. Instance Normalization: The Missing Ingredient for Fast Stylization;
5. Group Normalization;
6. Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization;