[人工智能]【机器学习】sklearn——线性回归

【参考：scikit-learn中文社区】
学习原理，学习案例，学习API参数

本文参考（从零开始）《机器学习的数学原理和算法实践》

这篇文章也不错【参考：机器学习 | 算法笔记- 线性回归（Linear Regression） - eo_will - 博客园】

【参考：公式里面的arg是什么意思？_一个做图像文本的深度学习人-CSDN博客】

术语

MAE(mean square error) 均方误差 又称 残差

原理

基本形式$f(x)=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$

向量形式 $f(x)={\omega \text{ω}\omega }^{T}x+b$

其中 $\omega \text{ω}\omega =(w_1,w_2,...w_d)$

目标：寻找最佳的$\omega \text{ω}\omega$和b

过拟合

正则化：给原来的损失函数增加惩罚项

实践

波士顿房价预测

# 导入数据集
from sklearn.datasets import load_boston

boston_house=load_boston()

# 特征变量与目标变量
x=boston_house.data
y=boston_house.target

from sklearn.model_selection import train_test_split
# 数据分割 25%作为测试集
x_train,x_test,y_train,y_test = 
			train_test_split(x,y,random_state=33,test_size=0.25)

# 线性回归模型
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化模型
lr=LinearRegression()
# 训练
lr.fit(x_train,y_train)
# 对测试集进行预测
lr_y_predict=lr.predict(x_test)

from sklearn.metrics import mean_squared_error
# 模型效果评估
# 比较测试集数据的预测值与真实值的差距多大，这里用均方误差来衡量
print("MSE:",mean_squared_error(y_test,lr_y_predict))

pycharm jupyter 输出

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

MSE: 25.096985692067754

官方

【参考：sklearn.linear_model.LinearRegression-scikit-learn中文社区】

• 有很多例子
  

>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
>>> # y = 1 * x_0 + 2 * x_1 + 3
>>> y = np.dot(X, np.array([1, 2])) + 3
>>> reg = LinearRegression().fit(X, y)
>>> reg.score(X, y)
1.0
>>> reg.coef_
array([1., 2.])
>>> reg.intercept_
3.0000...
>>> reg.predict(np.array([[3, 5]]))
array([16.])

【参考：线性回归实例-scikit-learn中文社区】

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)

# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]

# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20] # [0,第倒数二十个)
diabetes_y_test = diabetes_y[-20:] # [第倒数二十个,末尾｝

# Create linear regression object
regr = linear_model.LinearRegression()

# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)

# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)

# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print('Mean squared error: %.2f'
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination: %.2f'
      % r2_score(diabetes_y_test, diabetes_y_pred))

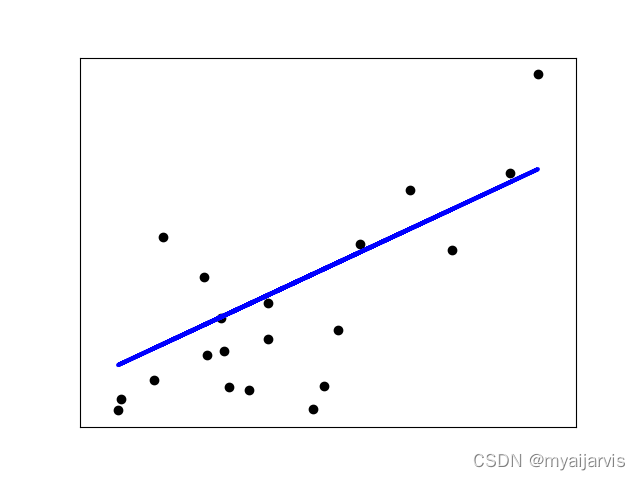
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()

Coefficients: 
 [938.23786125]
Mean squared error: 2548.07
Coefficient of determination: 0.47