前言
在进行CTR(click through rate)预估时,除了单个特征外,通常要进行特征组合,FM算法是进行特征组合时的常见算法。
因子分解机(Factorization Machine),是由Konstanz大学(德国康斯坦茨大学)Steffen Rendle(现任职于Google)于2010年最早提出的一种基于矩阵分解的机器学习算法,旨在解决大规模稀疏数据下的特征组合问题。
1、 FM 简介
1.1 特征工程
-
为什么要考虑特征之间的关联信息?
大量的研究和实际数据分析结果表明:
某些特征之间的关联信息(相关度)对事件结果的的发生会产生很大的影响。从实际业务线的广告点击数据分析来看,也证实了这样的结论。 -
如何表达特征之间的关联?
表示特征之间的关联,最直接的方法的是构造组合特征。样本中特征之间的关联信息在one-hot编码和浅层学习模型(如LR、SVM)是做不到的。目前工业界主要有两种手段得到组合特征:- 人工特征工程(数据分析+人工构造);
- 通过模型做组合特征的学习(深度学习方法、FM/FFM方法)

从上面公式中看出,一般的线性模型是不考虑特征间的关联的,为了描述特征间的多样性,我们采用多项式模型。在多项式中,特征x_i 和x_j 的组合用x_ix_j 表示,现在讨论二阶多项式模型。
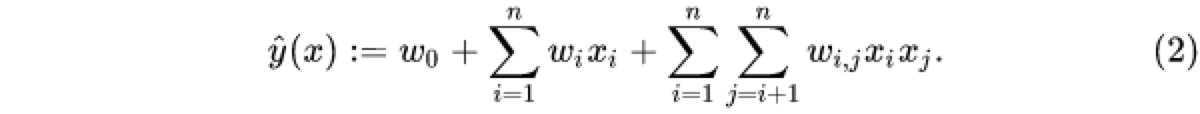
其中,n表示样本的特征数量,x_i表示第i个特征。公式的第三项就是加入了特征组合的部分。
公式2的形式确实是考虑了二阶特征组合对模型预测的影响,但同时会带来一个新的问题。因为在CTR预估问题里面,或者很多分类、回归问题里面,我们常常需要对类别型特征进行one-hot编码(比如男性、女性分别被编码为01,10),当类别型特征变量较多的情况下,编码后其实是会产生了高维特征。
1.3 one-hot的问题
-
FM主要是为了解决数据稀疏的情况下,特征组合问题。
一般categories特征经过one-hot编码以后,样本数据会变得很稀疏,假设有10万个item,如果对item的这个维度进行one-hot编码,这个维度的数据稀疏性就是十万分之一,所以数据的稀疏性,是实际应用中常见的挑战。 -
one-hot编码的另一个问题是特征空间变大,上面的10万个item,编码后样本空间有一个categories会变成10万维,特征空间会暴增。
2、FM模型求解:


3、实战
import numpy as np
import pandas as pd
import time
from matplotlib.font_manager import FontProperties
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
# 将预测值映射到0~1区间,解决指数函数的溢出问题
def sigmoid(x):
if x >= 0:
return 1 / (1 + np.exp(-x))
else:
return np.exp(x) / (1 + np.exp(x))
# 计算logit损失函数
def logit(y, y_hat):
z = y * y_hat
if z >= 0:
return np.log(1 + np.exp(-z))
else:
return np.log(1 + np.exp(z)) - z
# 计算logit损失函数的外层偏导数(不对y_hat本身求导)
def df_logit(y, y_hat):
return sigmoid(-y * y_hat) * (-y)
'''
# FM的模型方程:LR线性组合+特征交叉项组合 = 一阶线性组合 + 二阶线性组合
参数说明:
w_0:FM模型的偏执系数
W:FM模型的一阶特征组合权重系数 n *1
V:FM模型的二阶特征组合权重系数 n * k
'''
def FM(X_i, w_0, W, V):
# 样本X_i的特征分量xi和xj的2阶交叉项组合系数wij = xi和xj对应的隐向量Vi和Vj的内积
# 向量形式:Wij=<Vi,Vj> * xi * xj
interaction = np.sum((X_i.dot(V)) ** 2 - (X_i ** 2).dot(V ** 2)) / 2
y_hat = w_0 + X_i.dot(W) + interaction
return y_hat[0]
# SGD更新FM模型的参数列表,[w_0, W, V]
def FM_SGD(X, y, k=2, alpha=0.02, iter=45):
# m:用户数量,n:特征数量
m, n = np.shape(X)
# w_0,W参数初始化
w_0, W = 0, np.zeros((n, 1))
# 参数V初始化: V=(n, k)~N(0,1)
V = np.random.normal(loc=0, scale=1, size=(n, k))
# SGD结束标识
flag = 1
# 前一次迭代的总损失值
loss_total_old = 0
# FM模型的参数列表[w_0, W, V]
all_FM_params = []
# SGD开始时间
st = time.time()
# SGD结束条件1:满足最大迭代次数
for step in range(iter):
# 本次迭代的总损失值
loss_total_new = 0
# 遍历训练集
for i in range(m):
# 计算第i用户的预测值
y_hat = FM(X[i], w_0=w_0, W=W, V=V)
loss_total_new += logit(y[i], y_hat)
# logit损失函数的外层偏导数
df_loss = df_logit(y[i], y_hat)
# logit损失函数对w_0的偏导数
df_w0_loss = df_loss
# 更新参数w_0
w_0 = w_0 - alpha * df_w0_loss
# 遍历所有特征
for j in range(n):
# 若第i个用户在第j个特征取值为0, 则不执行参数更新
if X[i, j] == 0:
continue
# logit损失函数对Wij的偏导数
df_Wij_loss = df_loss * X[i, j]
# 更新参数W[j]
W[j] = W[j] - alpha * df_Wij_loss
# 遍历k维隐向量Vj
for f in range(k):
# logit损失函数对Vjf的偏导数
df_Vjf_loss = df_loss * X[i, j] * (X[i].dot(V[:, f]) - X[i, j] * V[j, f])
# 更新参数V[j, f]
V[j, f] = V[j, f] - alpha * df_Vjf_loss
# SGD结束条件2:损失值过小,跳出
if loss_total_new < 1e-2:
flag = 2
all_FM_params.append([w_0, W, V])
print("the total step:%d\n the loss is:%.6f" % ((step+1), loss_total_new))
break
# 第一次迭代,不计算前后损失值之差
if step == 0:
loss_total_old = loss_total_new
continue
# SGD结束条件3:前后损失值之差过小,跳出
if (loss_total_old - loss_total_new) < 1e-5:
flag = 3
all_FM_params.append([w_0, W, V])
print("the total step:%d\n the loss is:%.6f" % ((step + 1), loss_total_new))
break
else:
loss_total_old = loss_total_new
if step % 10 == 0:
print("the step is :%d\t the loss is:%.6f" % ((step+1), loss_total_new))
all_FM_params.append([w_0, W, V])
# SGD结束时间
et = time.time()
print("the total time:%.4f\nthe type of jump out:%d" % ((et - st), flag))
return all_FM_params
# FM模型进行预测
def FM_predict(X, w_0, W, V, ):
m = X.shape[0]
# sigmoid函数阙值设置
predicts, threshold = [], 0.5
# 遍历测试集
for i in range(m):
# X[i]的预测值
y_hat = FM(X_i=X[i], w_0=w_0, W=W, V=V)
# 分类非线性映射
predicts.append(-1 if sigmoid(y_hat) < threshold else 1)
return np.array(predicts)
# 计算预测准确度
def accuracy_score(Y, predicts):
# 预测准确数量
hits_count = 0
for i in range(Y.shape[0]):
if Y[i] == predicts[i]:
hits_count += 1
score_acc = hits_count / Y.shape[0]
return score_acc
# 根据FM模型每次迭代得到的参数[w_0, W, V]描绘预测准确率及损失值变化曲线
def draw_research(all_FM_params, X_train, y_train, X_test, y_test):
# loss_total_all记录使用每次迭代参数计算的损失值
# acc_total_all记录使用每次迭代参数计算的预测准确度
loss_total_all, acc_total_all = [], []
# 遍历每次迭代生成的参数值
for w_0, W, V in all_FM_params:
loss_total = 0
# 计算使用某一参数得到的总损失
for i in range(X_train.shape[0]):
loss_total += logit(y=y_train[i], y_hat=FM(X_i=X_train[i], w_0=w_0, W=W, V=V))
loss_total_all.append(loss_total / X_train.shape[0])
acc_total_all.append(accuracy_score(Y=y_test, predicts=FM_predict(X=X_test, w_0=w_0, W=W, V=V)))
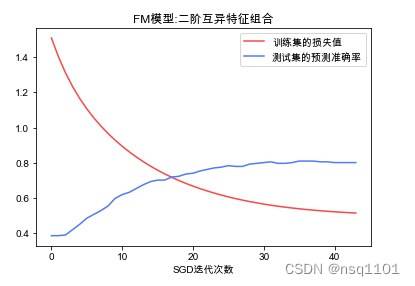
# 描绘训练集损失值的变化曲线
plt.plot(np.arange(len(all_FM_params)), loss_total_all, color='#FF4040', label='训练集的损失值')
plt.plot(np.arange(len(all_FM_params)), acc_total_all, color='#4876FF', label='测试集的预测准确率')
plt.xlabel("SGD迭代次数")
plt.title("FM模型:二阶互异特征组合")
# 给图像加图例
plt.legend()
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
plt.show()
if __name__ == '__main__':
# 产生一个随机序列
np.random.seed(123)
data = pd.read_csv("xg.csv", sep=',')
# 将数据集中的Class特征中的值0映射为-1,1映射为1
data['Class'] = data['Class'].map({0: -1, 1: 1})
# 切分数据集为训练集、测试集
X_train, X_test, y_train, y_test = train_test_split(data.iloc[:, :-1].values, data.iloc[:, -1].values, test_size=0.3, random_state=123)
# 训练集归一化处理
X_train = MinMaxScaler().fit_transform(X_train)
# 测试集归一化处理
X_test = MinMaxScaler().fit_transform(X_test)
# FM模型的参数列表[w_0, W, V]
all_FM_params = FM_SGD(X_train, y_train, k=2, alpha=0.01, iter=45)
# 最终的参数值w_0, W, V
w_0, W, V = all_FM_params[-1]
# 测试集的预测结果
predicts = FM_predict(X_test, w_0=w_0, W=W, V=V)
# 预测的准确度
acc = accuracy_score(Y=y_test, predicts=predicts)
print("测试集的预测准确度:%04f" % acc)
draw_research(all_FM_params, X_train, y_train, X_test, y_test)
结果展示
the step is :11 the loss is:300.793261
the step is :21 the loss is:284.074198
the step is :31 the loss is:275.387999
the step is :41 the loss is:271.465615
the total time:2.0634
the type of jump out:1
测试集的预测准确度:0.800866
4、 总结
-
FM降低了特征组合项学习不充分的影响。
参数学习有之前学习Wij的过程,变成了学习n个单特征对应的k维隐向量的过程。 -
FM提高了预估能力
由于FM学习的参数为单特征的隐向量,所以训练集中没有出现的特征组合的样本,FM模型依然可以用来预估。 -
FM提高了参数学习效率
参数个数由(n^2+n+1) 变成了(nk+n+1) 个,模型复杂的由O(mn^2) 变为O(mnk),m为训练样本数。 -
应用场景

-
FM是一个可以表示特征之间关系的函数表达式,可以推广到更高阶,将多个特征之间的关联信息考虑进来
-
FM模型对稀疏数据有更好的学习能力,通过交互项可以学习特征之间的关联关系,并且保证了学习效率和预估能力。