一、简单功能实现?
代码来源:卡尔曼滤波_周先森爱吃素的博客-CSDN博客_卡尔曼滤波的步骤
?注意:第34行和第35行的代码区别。34行为矩阵点乘,不是矩阵乘法。
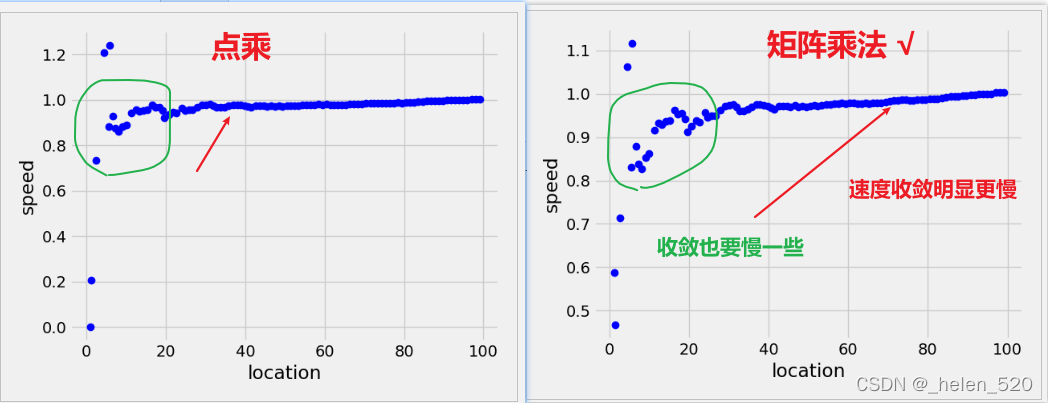
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 图1
?代码如下:
"""
Author: Zhou Chen
Date: 2020/3/27
Desc: 使用卡尔曼滤波进行状态预测
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# 创建位置观测矩阵,表示0-99的位移
z_observed = np.arange(100)
# 创建高斯噪声矩阵
np.random.seed(0)
z_noise = np.random.normal(0, 1, 100)
z = z_observed + z_noise
# 创建初始状态矩阵Xn|n
x = np.array([[0, ], [0, ]])
# 创建初始状态协方差矩阵P,这里的1也可以是一个较为合适的较大数字 Pn|n
p = np.array([[1, 0], [0, 1]])
# 创建状态转移矩阵,采样频率为1秒,所以△t为1 Fn transition
f = np.array([[1, 1], [0, 1]])
# 创建状态转移协方差矩阵,协方差较小 Qn
q = np.array([[1e-6, 0], [0, 1e-6]])
# 创建观测矩阵 Hn
h = np.mat([1, 0])
# 创建观测噪声的协方差矩阵 Rn
r = np.mat([1])
for i in range(100):
# 迭代,计算5大步骤
x_predict = f * x
# p_predict = f * p * f.T + q
p_predict = (f.dot(p)).dot(f.T) + q
kalman = (p_predict * h.T) / (h * p_predict * h.T + r)
x = x_predict + kalman * (z[i] - h * x_predict)
p = (np.eye(2) - kalman * h) * p_predict
plt.plot(x[0, 0], x[1, 0], 'bo')
plt.xlabel("location")
plt.ylabel("speed")
plt.savefig("rst.png")
plt.show()
二、残差分析
此处的:X=(posx, Vx)一维情况,x的位置,x方向的速度。
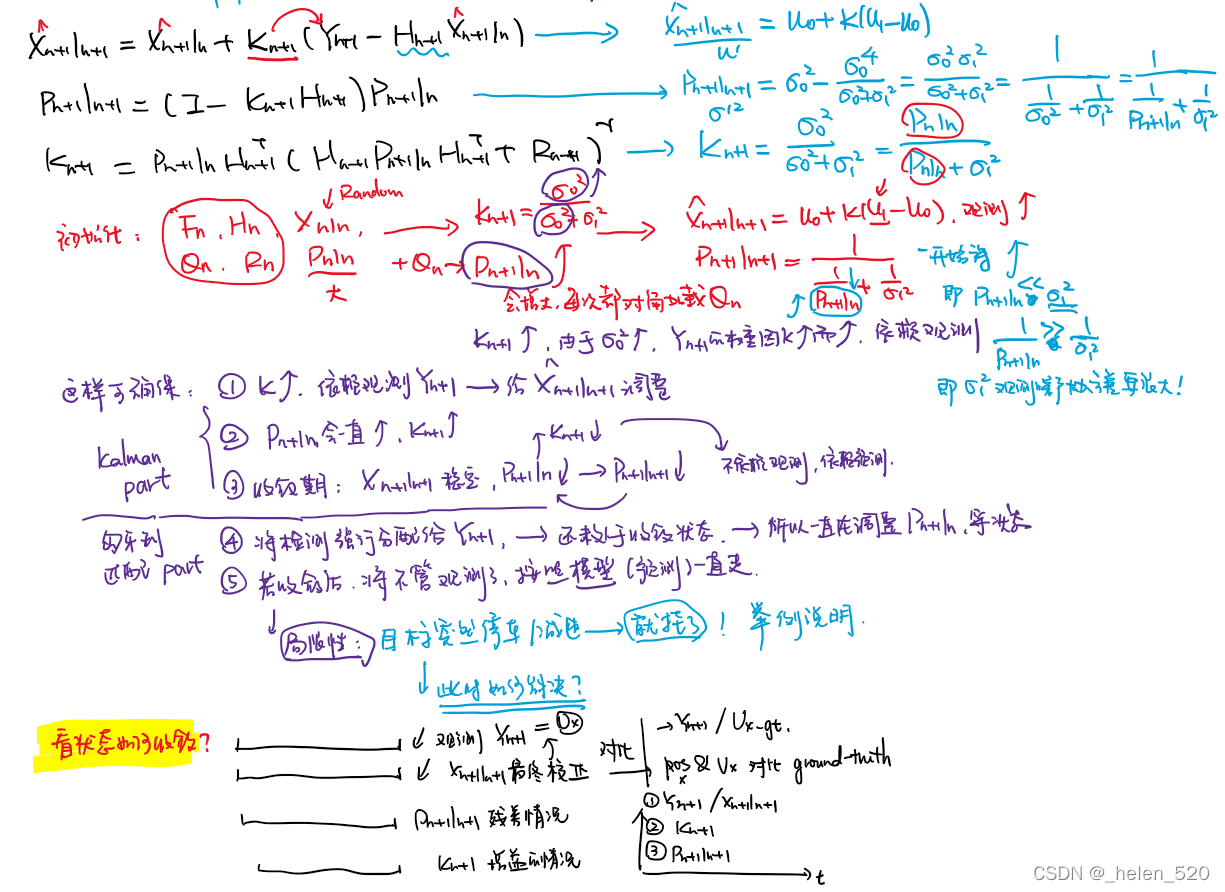
观测 vx=1. Yn+1 = x + vx * Δt + noise 状态 X=(posx, vx) 初始化:Pn|n, Xn|n,Hn, Fn, Qn=1e-6, Rn=1?




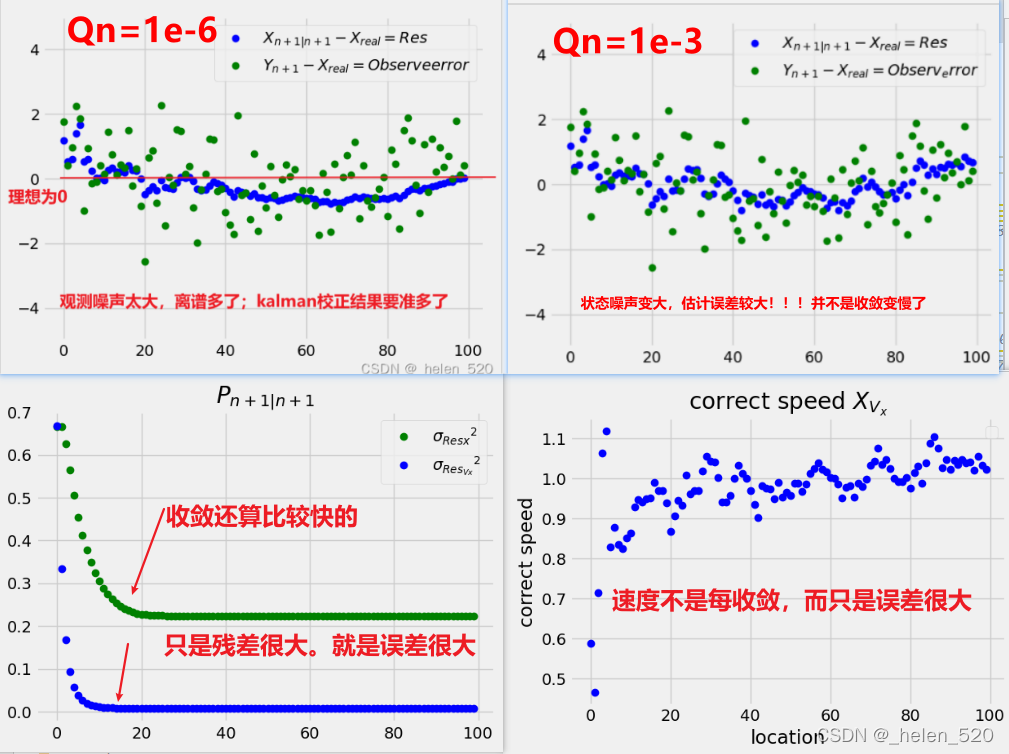
?从上图可以看出:
① kalman校正的(蓝色点)更加接近真实值。这也是观测越来越权重小的表现
②观测Yn+1(绿色点) 由于观测误差Rn=1,值太大了。所以观测误差较大
③速度的估计情况(红色点)速度的估计误差要远小于位移的估计误差。
因为速度的协方差更小,而位移的观测协方差较大一些。
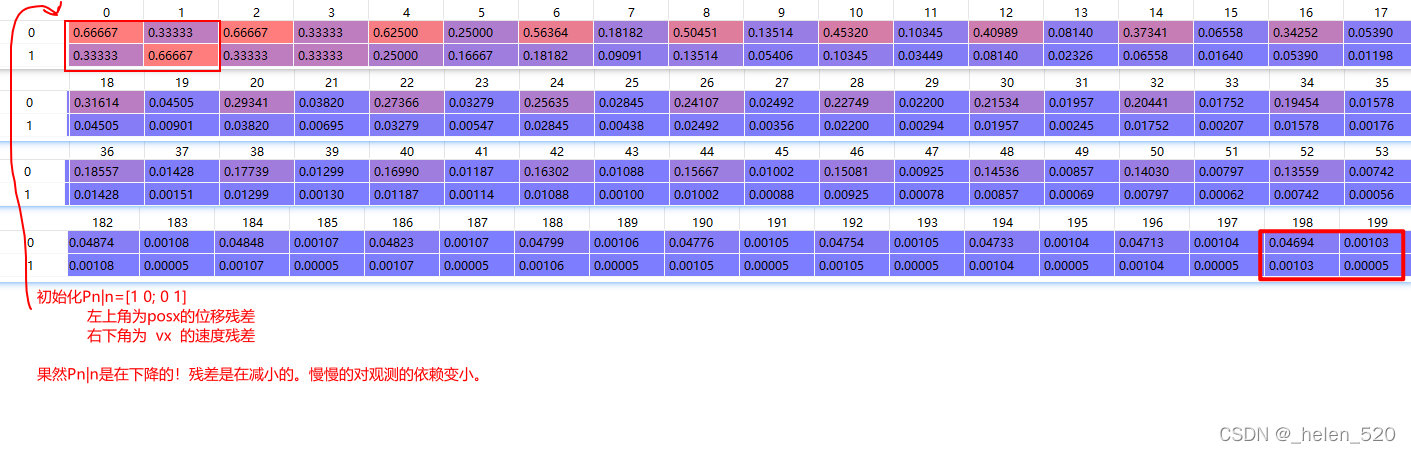
2.1 Pn|n误差协方差的变化情况
Pn|n 残差协方差的变化情况。位置残差 >> 速度残差?
观测噪声协方差为E(WnWn^T)=1,>>>? ?过程噪声1e-6。? ?意味着观测十分不准。
可以调节观测噪声协方差 MeasurementNoiseCov的值,确定观测到底准不准,来调节收敛速度?
?,对角线上值的变化情况,反对角线上的位置的值是相同的,在上述表格中可以看出来。所以Pn+1|n+1是实对称矩阵的。
?位移残差的协方差是在不断减小的,速度残差的协方差也在减小。但是位移比速度的协方差大一些

?原因:位移残差 >> 速度残差的原因。


2.2 增益的变化情况
 ?2.3 初始化分析
?2.3 初始化分析
---------------------------
?3. 参数改变
3.1 将观测噪声变小
?观测噪声减少之后,kalman收敛速度大大加快!!!
z_noise = np.random.normal(0, 0.1, 100) r = np.mat([0.1])

?3.2 状态噪声Qn变大
?将Qn变为[1e-3,0;0 1e-3],Rn=1。Vn~N(0,Qn),这样Vn的范围就为:小数点后两位波动

?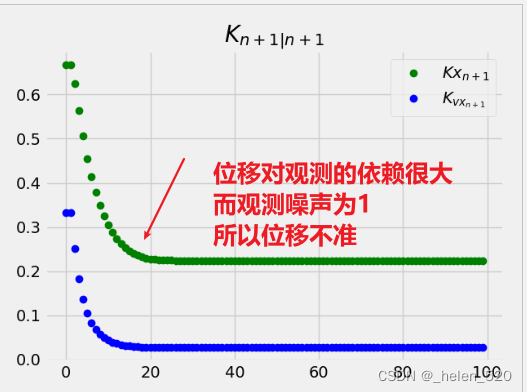
问题:为什么Kxv=0速度增益为0了,而速度预测还是震荡状态?
-
?v=v预测+kvx*观测。kvx=0,那就只有预测就是不准的。
-
x就是不准的。不准就是:Vn的原因,就是状态噪声导致的。Vn在小数点后两位波动,那么得到的速度v就一直在速度1上加减一个Vn,所以就是上面所示的抖动状态!!!!!?破案了

3.3 为什么Kvx增益部分为0,怎么着都会为0
![]() ?
?
?这是一个很有意思的问题!!!!!!
上面的代码部分:x_predict=2×1矩阵,kalman增益2×1,但是h是1×2,h*x_predict=1×2 * 2×1=1×1,所以是一个数。然后kalman×数=2×1,那么x=(posx, vx),怎么就加上了观测z[i]呢!!!!!!
其实是这样的!!!!? ?最后的kalman增益(Kx, Kvx)的第二项Kvx会迭代为0,v=常数了,所以速度会迭代到1。所以这个公式是完全没有问题的!!!!!!!!!不用怀疑Kalman*常数的问题!!!!
4.?一些问题思考
- 即使观测噪声很大,E(WnWn^T)=1,过程噪声1e-6,仍然可以实现收敛后,完全依赖于kalman校正。不用太担心依赖于观测。参考上方的图5
- 如果状态噪声比较大的话,Qn比较大。就会影响K的值,kalman校正的结果的权重变小。观测的权重会上升。Qn变大,K会变大。
- Rn变大,收敛慢了。参考上面图8
Qn较小,就算观测Rn变大。最后都会依赖于预测。只不过收敛的速度变慢了。
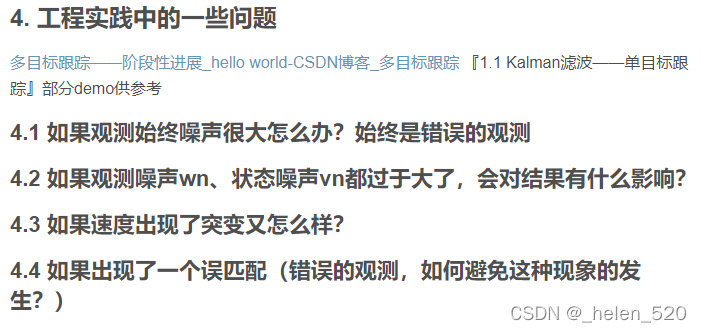
4.4 如果出现了误匹配
可能的解决方法:
- 判断检测detection与上一帧预测的位置的欧氏距离。以及,此帧预测 与 上帧估计的距离。
如果这两个距离相差很大,那说明观测出现了很大问题。至于为什么会匹配,肯定是因为匹配除了问题。用于判断匹配的结果到底是否正确!!! - 剔除匹配,此帧还是按照预测来!!!在match中再去判断一下是否匹配,可以筛选出很离谱的匹配。甚至可以通过方向来判断,角度;也可以通过速度来判断,是否突然加速了那么多!!!
- metric:欧氏距离、速度、方向;进一步剔除误匹配的
- 漏匹配的靠:预测维持!
-------------------------------------------
?代码如下:
"""
Author: Zhou Chen
Date: 2020/3/27
Desc: 使用卡尔曼滤波进行状态预测
"""
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# 创建位置观测矩阵,表示0-99的位移
z_observed = np.arange(100) # 观测 vx=1. Yn+1 = x + vx * Δt + noise
# 创建高斯噪声矩阵
np.random.seed(0)
z_noise = np.random.normal(0, 1, 100)
z = z_observed + z_noise # 观测
# 创建初始状态矩阵Xn|n=[posx, vx]
x = np.array([[0, ], [0, ]])
# 创建初始状态协方差矩阵P,这里的1也可以是一个较为合适的较大数字 Pn|n
p = np.array([[1, 0], [0, 1]]) # Pn|n=[resx,0;0 resVx]
# 创建状态转移矩阵,采样频率为1秒,所以△t为1 Fn transition
f = np.array([[1, 1], [0, 1]])
# 创建状态转移协方差矩阵,协方差较小 Qn=[σx^2 0;0 σvx^2]
q = np.array([[1e-6, 0], [0, 1e-6]])
# 创建观测矩阵 Hn
h = np.mat([1, 0])
# 创建观测噪声的协方差矩阵 Rn = E(WnWn^T)=E(z_noise),normal(0,1)均值为0,方差为1
r = np.mat([1])
for i in range(100):
# 迭代,计算5大步骤
x_predict = f * x
# p_predict = f * p * f.T + q
p_predict = (f.dot(p)).dot(f.T) + q
kalman = (p_predict * h.T) / (h * p_predict * h.T + r)
x = x_predict + kalman * (z[i] - h * x_predict)
p = (np.eye(2) - kalman * h) * p_predict
# x[0,0]为预测位置,posx,x[1,0]为vx
plt.plot(z_observed[i], x[1, 0], 'bo',linewidth=1.0)
# 这里的真是画图应该为:(t, posx, posx-gt) (t, vx, vx-gt=1)
# (t, Pn+1|n=1残差变化情况) (t, Kn+1)增益依赖Yn+1观测的变化情况
if i==0:
p_stack = p
k_stack = kalman
x_pos = x[0, 0]
x_speed = x[1, 0]
else:
p_stack = np.hstack((p_stack, p))
k_stack = np.hstack((k_stack, kalman))
x_pos = np.vstack((x_pos, x[0,0]))
x_speed = np.vstack((x_speed, x[1,0]))
plt.xlabel("location")
plt.ylabel("correct speed")
plt.title("correct speed $X_{V_x}$")
plt.legend()
# plt.savefig("rst.png")
plt.show()
plt.figure()
plt.plot(z_observed, x_pos, 'o', color='blue', label='kalman correcnt')
plt.plot(z_observed, z_observed, 'x', color='green',label='posx ground truth')
plt.legend()
plt.show()
plt.figure()
plt.plot(z_observed, x_pos.reshape(100)-z_observed, 'o', color='blue', label='$X_{n+1|n+1}-X_{real}=Res$')
plt.plot(z_observed, z-z_observed, 'o', color='green', label='$Y_{n+1}-X_{real}=Observ_error$')
plt.ylim(-5,5)
plt.legend()
# 设置坐标轴范围
plt.show()
plt.figure()
plt.title("$P_{n+1|n+1}$")
plt.plot(z_observed, np.array(p_stack[0,::2]).reshape(100), 'go', label='${\sigma_{Resx}}^2$')
plt.plot(z_observed, np.array(p_stack[1,1::2]).reshape(100), 'bo', label='${\sigma_{Res_{Vx}}}^2$')
plt.legend()
plt.show()
plt.figure()
plt.plot(z_observed, x_pos.reshape(100)-z_observed, 'o', color='blue', label='$X_{n+1|n+1}-X_{real}=Res$')
plt.plot(z_observed, z-z_observed, 'o', color='green', label='$Y_{n+1}-X_{real}=Observ_error$')
plt.plot(z_observed, x_speed.reshape(100) - 1, 'ro', label='$Xv_{n+1|n+1} - Xv_{real}=correct speed error$')
plt.ylim(-5,5)
plt.legend()
plt.show()
a = a + 1