[人工智能]【吴恩达机器学习】第七周课程精简笔记——无监督学习和降维

Unsupervised Learning

1. Clustering

（1）Unsupervised learning introduction

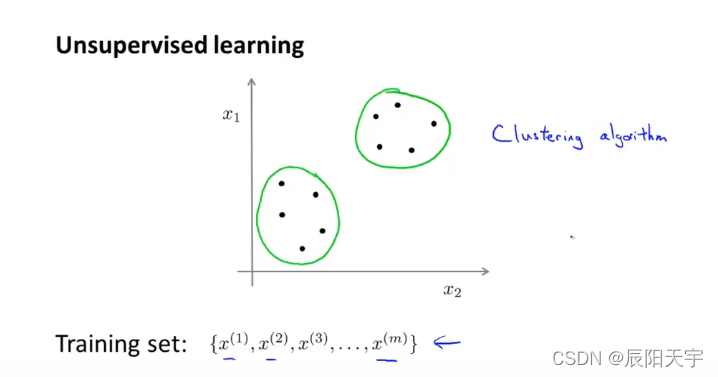
无监督学习是针对一组无标签数据集，用算法找到一些隐含在数据中的结构。图中显示出，我们可以用算法找出两簇数据。这些簇的算法也称为聚类算法。

（2）K-means algorithm

在聚类算法中，我们会给定一组未加标签的数据集。同时，我们也希望能够自动地将这些数据分成有紧密关系的子集或簇。

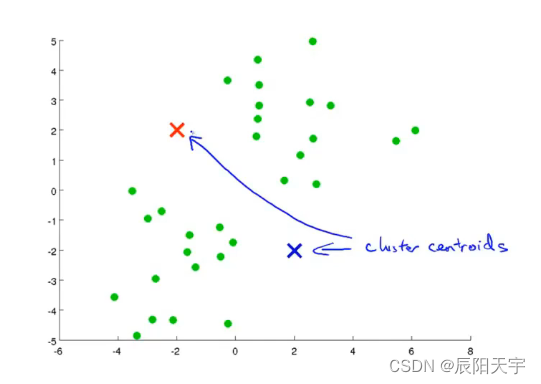
（1）先确定要将数据分为几个类别，也就是K的大小，图中示例是将数据分成两个类，K=2。
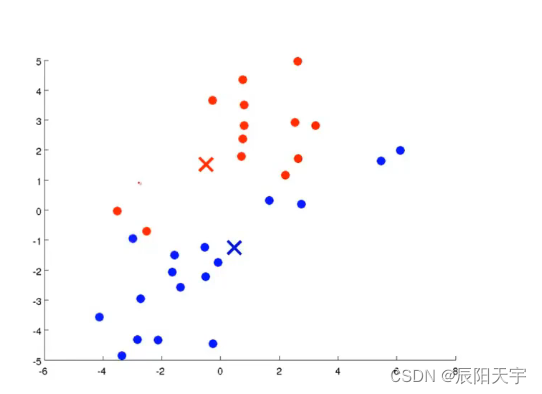
（2）选择两个数据点作为初始聚类中心，然后遍历每个绿色点距离这两个点中哪个点更近，就将绿色的点划分为哪种类别。

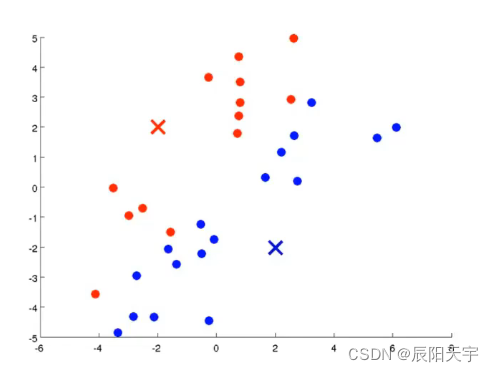
（3）将各点归属的簇划分好后，计算各个簇中心（质心），也就是各个点的均值，重新得到新的簇中心。

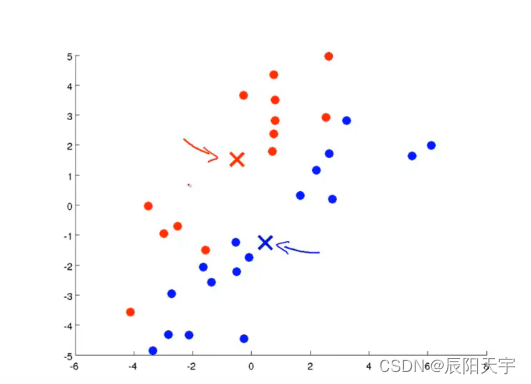
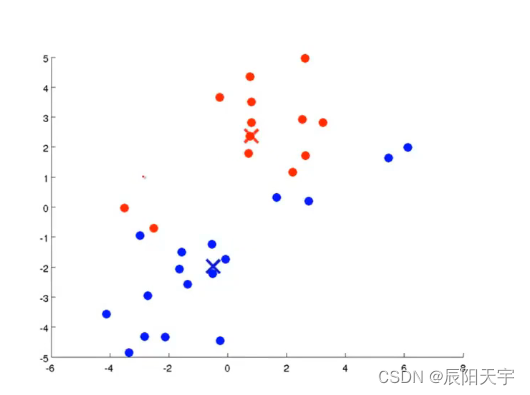
（4）得到新的簇中心，也就是新的均值后。再对所有的点进行遍历，查询各个点离这哪个聚类中心更近，就将其重新划分于该类别内。

（5）不断重复第（4）步和第（5）步，直至聚类中心不再有变化并且各点的所属类别也不再改变。



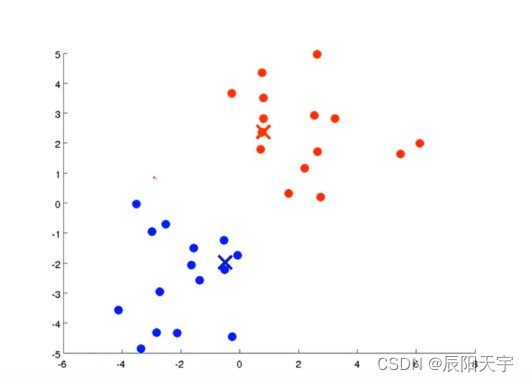
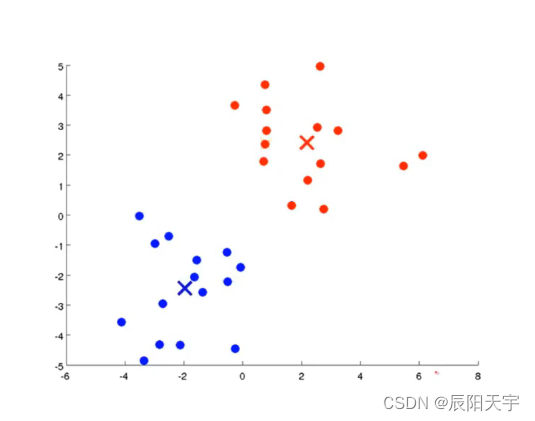
（6）当聚类中心不再有变化并且各点的所属类别也不再改变时，我们可以认为已聚合完成。

$随机选取K个聚类中心{\mu }_1,{\mu }_2,...,{\mu }_k\in {\mathbb{R}}^n$
R e p e a t { f o r ? i = 1 ? t o ? m c ( i ) : = 1 到 K 个 聚 类 中 心 中 最 接 近 于 x i 的 聚 类 中 心 的 索 引 号 f o r ? k = 1 ? t o ? K μ k : = 第 k 个 聚 类 所 分 配 点 的 均 值 （ 聚 类 中 心 ） } Repeat \{ \\ \quad for \ i = 1 \ to \ m \\ \quad \quad c^{(i)} := 1到K个聚类中心中最接近于x^{i}的聚类中心的索引号 \\ \quad for \ k = 1 \ to \ K \\ \quad \quad \mu_k := 第k个聚类所分配点的均值 （聚类中心）\\ \} Repeat{for?i=1?to?mc(i):=1到K个聚类中心中最接近于xi的聚类中心的索引号for?k=1?to?Kμk?:=第k个聚类所分配点的均值（聚类中心）}

其中计算点与聚类中心的距离常用方式是 $\underset{k}{\min }||x^{(i)}?{\mu }_k|{|}^2$，计算聚类中心的常用方式是求平均值。

如果出现一个聚类中心，该聚类中没有其余点。那么常用的方法是将该聚类中心移除，不过最后得到的会是K-1个聚类，而不是K个聚类。如果你一定要得到K个聚类的话，那么就将这个没有点的聚类中心删除，然后重新随机选取一个点作为聚类中心，再重复之前的方法是划分聚类即可。

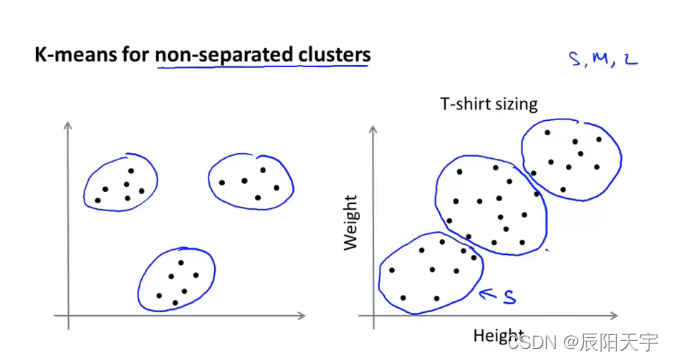
K-means算法对难以划分的聚类也可以进行划分，左侧显然很容易就划分出来，右侧使用K-means也可以划分出类似的三个簇类。

（3）Optimization objective（优化目标）

图中的代价函数称为失真函数，也称为K均值算法的失真。

$Reapat$ 中分为两步：
一步是聚类分布计算，通过代价函数，更新 $c^{(i)}$，得到每个数据点归属于哪个聚类。
另一步是移动聚类中心，通过另一个待机函数，更新 ${\mu }_i$，得到新的聚类中心。

（4）Random initialization

我们将学习到如何初始化K-means算法，如何使算法避开局部最优

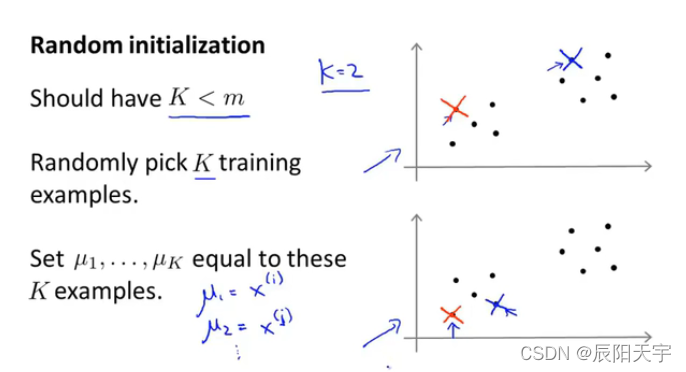
首先应该选取的k值要小于总样本数，然后再数据中随机选取k个训练样本作为初始化聚类中心。从第一和第二幅图中我们可以看到，选取不同的聚类中心，可能将会得到不同的结果。具体而言，K-means算法可能会落在局部最优解中。

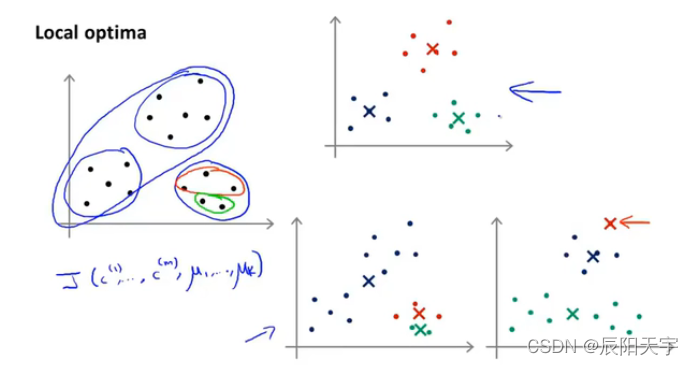
右上角的图中是K-means算法得到的全局最优解，找到了非常好的聚类结果。

右下角两幅图中，实际上是K-means算法落在了局部最优解当中，因此不能很好地最小化失真函数（distortion function）J。

如果你想要K-means算法避免落到局部最优解中，一种方式是尝试多次随机初始化，不是期望初始化一次就找到了全局最优解，而是通过初始化K-means算法多次并运行K-means算法多次，以此来保证我们最终能得到一个尽可能好的局部或全局最优解。

一般是要求K-mean算法运行到50-1000次。运行指定次数n次后，你会得到n个不同的结果，从中选取一个代价最小的作为最终结果，也就是失真值最小。

如果你用的K值足够小，比如2-10，那么通过多次随机初始化K-mean算法，就能够找到一个较好的局部最优解，保证你能找到更好的聚类。如果K值足够大，比如成百上千个聚类，那么多次随机初始化K-mean算法，对结果并不会有太大的改善。

（5）Choosing the number of clusters

目前为止没有找到非常好的选择聚类数量的方法，常用的还是观察可视化的图、观察聚类算法的输出等等。

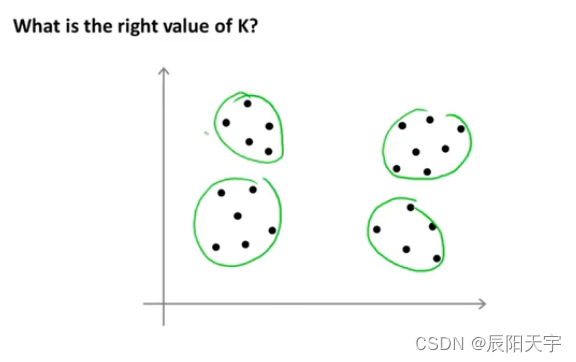
相同的一组数据分布，有的人可能会认为有四个聚类。

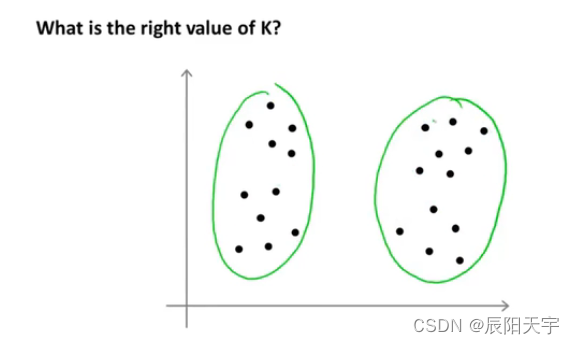
有的人却可能认为有两个聚类，真实的聚类可能相当地模棱两可，并不一定只有唯一一个确定的答案。这也是非监督学习的一个特性，因为数据没有标签，所以并不总是有一个明确的答案。正是因为这个原因，用一个自动化的算法来选择聚类数量是一个很困难的事情。

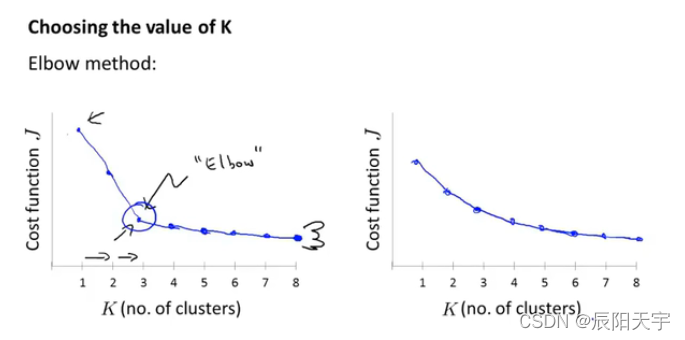
一个选取聚类数量的方式是“肘部法则”。左边这幅图中，可以看到随着K的选取逐渐增大，失真函数的值会逐渐减小。在2-3之间且靠近3的位置有一个拐点，在到达拐点之前，畸形函数会大幅度的减小，而在拐点之后，畸形函数的减小幅度却变的很小。我们便让K=3，这个拐点类似于人的“肘部”，这种选取方式也因此叫肘部法则。

肘部法则并不常用，因为在实际运用过程中，可能得到右边这幅图，较为均匀的曲线形式，从而导致不能很明确的找到一个明显“肘部”。

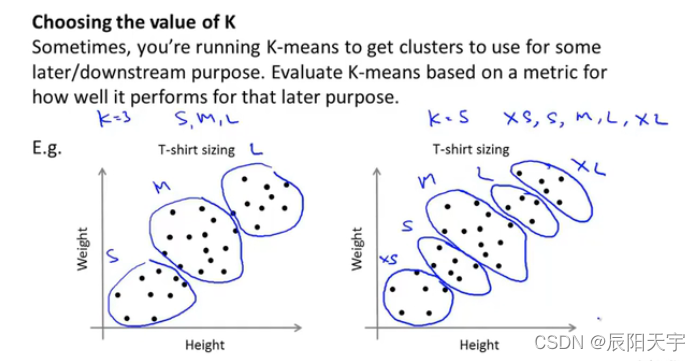
因为K-means算法通常是用来进行一些数据的处理，来为后续的选择提供参考。比如用于市场分割，用于选择生产不同产品的数量。因此，还有一种选择K的方式是看让K值等于多少能更好地应用于后续的目的。

总结一下K的选取还是通过人的手动输入、根据经验确定或者肘部法则选取。主要的核心还是要清楚，我们使用K-menas算法处理数据的的最终目的是什么，如何能更好地服务与后续的目的。

Dimensionality Reduction（降维）

1. Motivation

（1）Motivation I：Data Compression（数据压缩）

数据压缩不仅能压缩数据减少存储空间，还能够对学习算法进行加速。

如果你有成千上万的特征，你就可能迷失在到底应该用哪些特征。当你从不同的工程小组哪里获得特征后，将这些特征汇集起来后可能会出现高度冗余特征的现象。

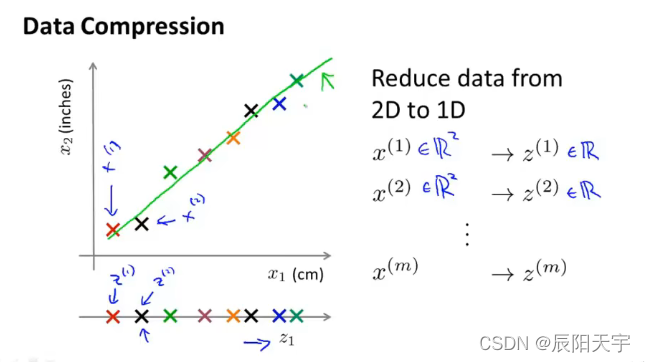
通过降维的方式，可以减少冗余特征。例如，将n+1维的数据映射到n维的数据中。将投影后得到的数据，来近似表示原始的数据集。图中是将二维数据，投影到一维空间中一条直线上，我们将此一维数据来近似表示原始的数据集，这样就能对内存的需求减少一半，同时可以让我们的学习算法更快。

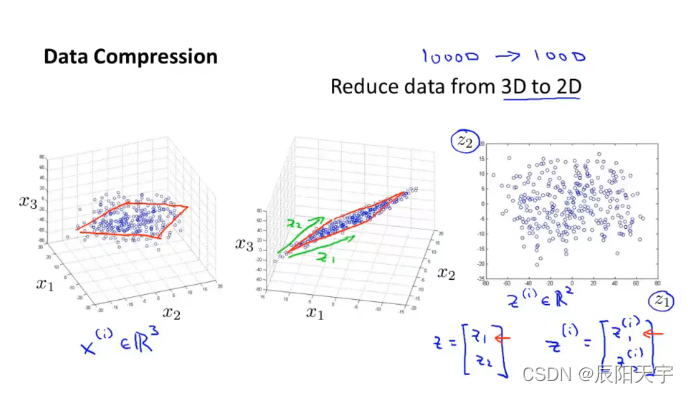
在实际中，我们可能需要将1000维的数据压缩成100维的数据。图中是将三维空间中的数据，投影到一个二维平面当中。对于这个二维平面，我们需要 $z_1$ 和 $z_2$ 两个轴来指定这个平面中点的位置。

（2）Motivation II：Data Visualization

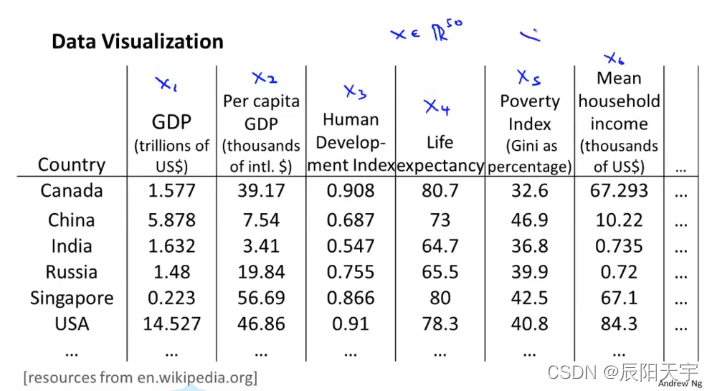
这里有50维的数据来描述不同的国家。

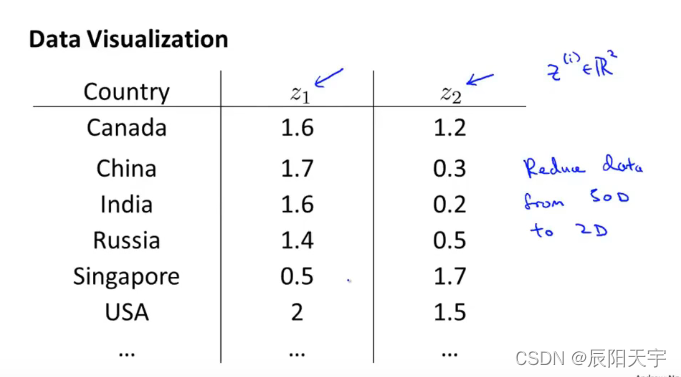
我们的目标是把这些国家在一个二维平面上表示出来，用两个特征 $z_1$ 和 $z_2$ 来描述一个国家。因此，我们需要将50维降到2维。

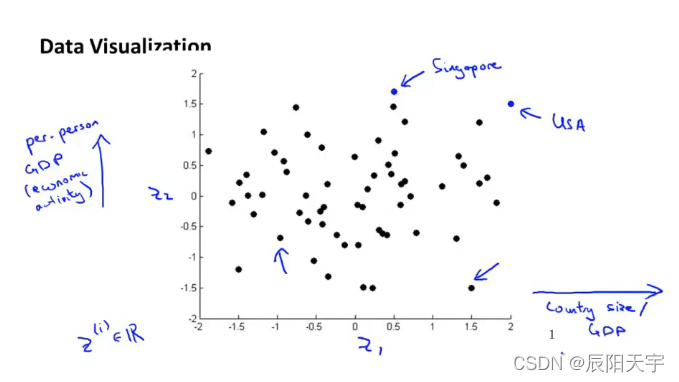
当你这样做时，你会发现z通常并不是一个具有实际物理意义的特征。将这些点可视化到二维平面上，每个点都代表一个国家，可以发现这些点随着两个坐标轴的变化而带的不同的变化。会存在与某些物理意义相关的联系，例如GDP、国民人均收入、环境等等。

2. Principal Component Analysis（主成分分析）

（1）formulation（公式描述）

对于降维问题来说，现在最常用的一种方式是主成分分析方法PCA。

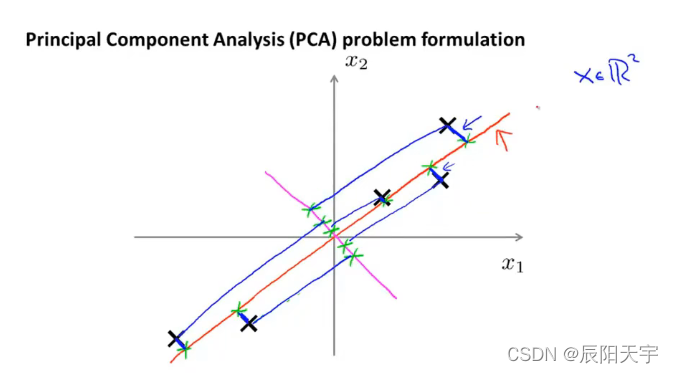
假设我们选取二维平面来降维，我们将二维平面上的点投影到这条红色直线上，绿色点是投影点。我们会发现每个原始点到它们投影直线上的点的距离是非常短的。PCA的做法是它会找到一个低维平面（本例是直线），然后将数据投影在上面，蓝色线段代表投影距离。目标是让蓝色线段的长度的平方最小，这些蓝色线段的长度有时也称为投影误差。

在使用PCA之前，常规的做法是先进行均值归一化（mean normalization）和特征缩放（feature scaling）使得特征 $x_1$ 和 $x_2$ 的均值为0并且其数值在可比较的范围之内。

如果我们有n维数据想要投影到k维平面上，我们需要将数据投影到k个方向的向量构成的线性子空间当中并且最小化投影误差。

注：同一条直线上，不同方向的向量不影响最终的投影误差。

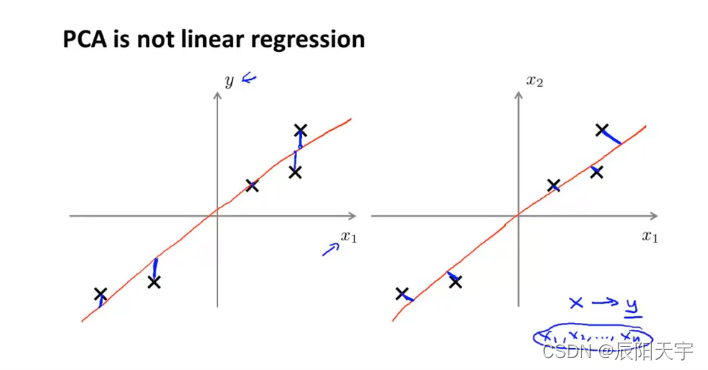
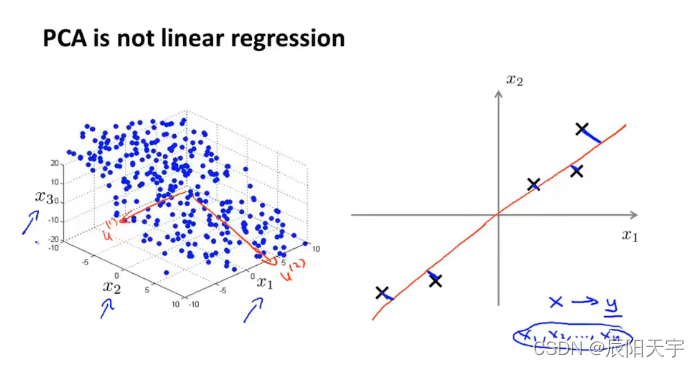
PCA并不是线性回归，即使它们看起来有一些相似，但它们是截然不同的算法。

在线性回归中，我们要拟合出一条直线，让点和直线之间的平方误差最小。因此，我们的策略是让点向坐标轴 $x_1$ 垂直方向到红色直线的距离最小，也就是让 $y?(w^{T}x+b)$ 误差最小。此外，线性回归的目的是用 $x$ 的线性组合去预测 $y$，因此 $x$ 与 $y$ 将会被作为不同的含义对待。

在PCA中，我们要拟合出一条直线，让点和直线之间的投影误差平方最小。因此，我们的策略是让点到直线的正交距离最短，也就是让点到红色直线的距离最短。此外，PCA的目的是实现降维，数据中没有 $y$ 这个概念，只有$x_1,x_2,...,x_n$，每个坐标轴都被赋予相同的地位来对待。

（2）PCA algorithm

在构建PCA算法之前，先对数据进行预处理

对于训练样本 $x$ 进行特征缩放或均值归一化，让 $x_j^{(i)}=\frac{x_j^{(i)}?{\mu }_j}{s_j}$ ，其中 $x_j^{(i)}?{\mu }_j$ 是为了让其分子的均值为0，而$s_j$ 是训练集中的某一测量值，比如最大值减最小值之差或者是训练集的方差。

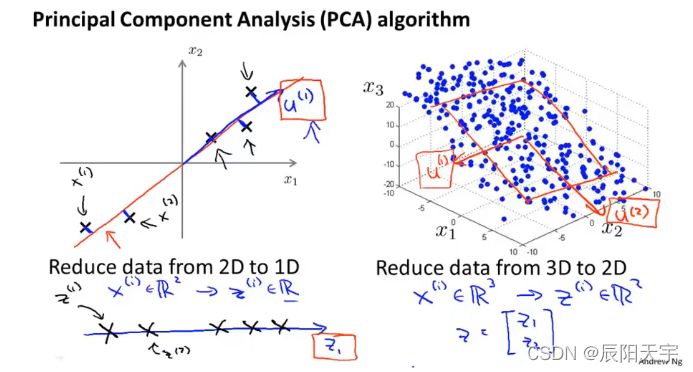
构建PCA算法时，我们的目标是找到一个更低维度的平面，来让点到该平面的平方距离和最小。我们要做的就是让 $x^{(i)}\in {\mathbb{R}}^2$ 降维成 $z^{(i)}\in {\mathbb{R}}^2$。因此，PCA算法是要计算出向量 $u^{(i)}$ 和向量 $z^i$。

PCA算法中，我们想把n维数据降到k维数据

我们首先是要计算协方差矩阵，这个矩阵用大写的sigma表示，尽管它和求和符合相同，但它并代表求和的意思，而是仅用来表示一个矩阵。（协方差矩阵总是满足正定矩阵）。

svd代表奇异值分解（singular value decomposition），这是一个更加高级的分级算法，这也是一个很高级的线性代数的应用。对我们来说主要有用的是包含特征向量的矩阵U，他会是一个 nxn 的矩阵，含有主成分。我们要做的是取前k个向量。而矩阵S是含有特征值的 nxn 的对角矩阵。

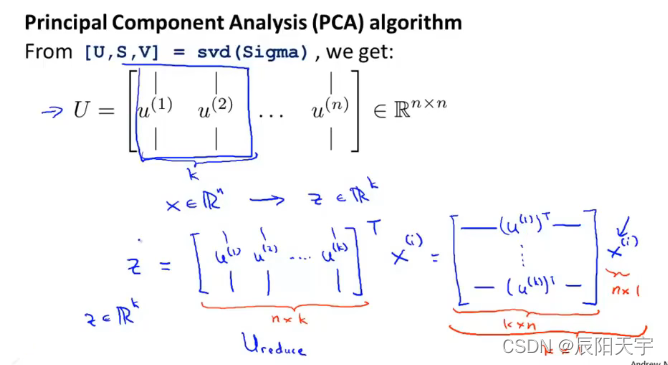
z矩阵等于n×k的矩阵再乘上nx1的矩阵

总而言之，这就是PCA算法。均值归一化保证每一个特征都是均值为0的任意特征缩放。预处理数据完之后，我们计算载体矩阵sigma。然后，我们使用svd函数得到U,S,V，我们可以得到将维度矩阵U的前k列，最后得到了一个从特征向量x到降维的表示z，注意这里 $x_0$ 不能为常数给它赋值1。

（3）Choosing the number of principal components（主成分数量选择）

在PCA算法中，我们让n维降到了k维，这个k也被称为主成分的数量。

• 投影的平方误差：$\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}?x_{approx}^{(i)}|{|}^2$
• 数据的总方差：$\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2$，也相当于是数据到原点的距离平方
• 一种常用的选择k的方式是选择一个较小的k，使得这两者之间的比值小于0.01，让投影平方误差除以数据的总方差：$\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}?x_{approx}^{(i)}|{|}^2}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2}\le 0.01$，我们要做的是比如说让这个比率小于0.01，也就是让99%的方差性被保留。

PCA算法：
Step 1：选择k=1
Step 2：计算 $U_{reduce},z^{(m)},x_{approx}^{(m)}$
Step 3：检查方差保留公式中是否满足规定的数值，如果不满足，则重新选择一个K再计算，直至到满足位置。

通过svd函数你可以获得一个对角矩阵s，通过计算 $1?\frac{{\sum }_{i=1}^k{s}_{ii}}{{\sum }_{i=1}^n{s}_{ii}}$ 可得到上面相同的检查方差保留率。

所以可以通过检测s的值来判断是否可以选择此k值

（4）Reconstruction from compressed representation（压缩重现）

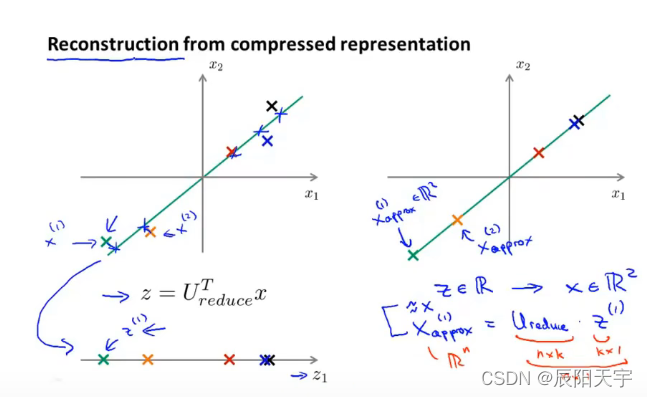
压缩重现要做的就是将压缩后的数据，再重新还原回近似于压缩前的原数据，回到未压缩时的数据表示。

目标是将 $z\in \mathbb{R}$ 还原回 $x\in {\mathbb{R}}^2$ ，也就是 $x_{approx}^{(i)}=U_{reduce}?z^{(i)}$ （因为 $U_{reduce}$ 具有正定性，因此为正交矩阵 $U^{T}U=U^{?1}U=E$），我们把这一过程叫做原始数据的重构。

（5）Advice for applying PCA

我们常常使用PCA对监督学习算法进行加速。

我们首先可以检查已被标记的训练集并抽取它们用作输入数据，其中仅抽取 $x$ 而不抽取 $y$，这样子就构建出了一组无标签的数据集。然后，我们使用PCA算法得到一组低维数据。这样，我们就得到了一组新的数据集。

注意：PCA算法做的是一个从 $x$ 到 $z$ 的映射，这个映射只能通过在训练集上运行PCA来定义。具体而言，PCA学习的这个映射所做的就是计算一系列参数，然后进行特征缩放和均值归一化，它还计算矩阵 $U_{reduce}$。 我们应该只在训练集上拟合这些数据，而不是在交叉验证集或测试集上。 当我们找到一些合适的参数后，我们可以把这个定义的从 $x$ 到 $z$ 的映射用在交叉验证集或者测试集的其他样本。

在许多问题上，我们可以减少较多维度的数据，比如1/5或者1/0，同时仍能保留大部分的方差并且几乎不影响性能（比如分类准确度等等）。使用这样子较低维度的数据，可以加速我们的学习算法。

总结一下，PCA有两个方面的应用。一个是压缩，对数据集进行特征压缩后，不仅可以减少我们使用的存储空间容量，还可以加速我们的学习算法。另一个是可视化，对于可视化的应用，我们通常选择k=2或者3。

对于过拟合现象，不建议使用PCA来进行解决。尽管在使用PCA后，可能对过拟合现象有一个良好的改善，但是使正则化是解决过拟合现象的一种更好的方法。

在使用PCA时，由于仅使用一组无标签数据 $x$，没有考虑 $y$ 的取值，同时还对数据进行了压缩，这样做可能会损失一部分有用信息。尽管设置方差保留率为99%或95%可能会有助于改善拟合现象，但事实证明使用正则化时，得到的效果和方差保留率为95%时的效果近乎一样好。

因此，我们建议使用正则化去解决过拟合现象。因为正则化考虑了 $y$ 的取值，并且不太可能会损失一些有用的信息。

最后，不应该滥用PCA算法。在使用PCA之前，建议先不用PCA而是使用原始数据集去运行算法，当这么直接做不能达到目的时才应开始去考虑使用PCA，来压缩特征，减少使用的内存空间或存储空间，加速训练速度。

Exercise 7：支持向量机SVM

【吴恩达机器学习】Week8 编程作业ex7——K-means聚类和PCA