[人工智能]旋转目标检测：The KFIoU Loss for Rotated Object Detection（Under review in ICLR 2022）

关键词：KFIoU, 倾斜IoU(SkewIoU)

参考博客：
https://zhuanlan.zhihu.com/p/447286823
论文原文下载：
https://openreview.net/pdf?id=B9LUI0pZFGc
代码下载地址：
mmrotation: https://github.com/open-mmlab/mmrotate

一、摘要（直译）：

不同于发达的水平目标检测区域，即基于计算友好的IoU的损失很容易被采用，并很好地符合检测指标。相比之下，旋转探测器通常涉及到基于SkewIoU的更复杂的损失，这对基于梯度的训练不友好。在本文中，我们认为一个有效的替代方法是设计一个近似损失，可以实现与SkewIoU损失的趋势水平对齐，而不是严格的值恒等。具体地说，我们将对象建模为高斯分布，并采用卡尔曼滤波来固有地模拟SkewIoU的定义机制，并在趋势水平上显示其与SkewIoU的对齐。这与最近基于高斯建模的旋转检测器形成了对比，例如GWD，KLD，它涉及到一个人为指定的分布距离度量，这需要额外的超参数调整。由此产生的被称为KFIoU的新损失与精确的SkewIoU相比更容易实现，工作得更好，这要归功于它的完全可微性和处理非重叠情况的能力，我们进一步将我们的技术扩展到三维情况。

二、针对的问题：

1、针对度量方式和损失函数不一致——提出一种基于卡尔曼滤波的倾斜IoU即KFIoU
2、解决边界不连续和类正方形问题——将旋转框转换到高斯分布
3、减少两个高斯分布间中心的距离——用center损失
4、通过卡尔曼滤波计算新位置中两个区域的重叠
5、作者讲该技术从二维扩展到三维空间

三、相关工作：

1、旋转物体检测领域：
（1）扩展经典的水平探测器（extend classical horizontal detectors）——采用旋转边界框（adopting the rotated bounding boxes）
（2）针对航空图象（Aerial images）物体任意定向（arbitrary-oriented）和密集分布的大高宽比（dense-distributed with large aspect ratios）
——one-stage: ICN, ROI-Transformer, SCRDet, Mask OBB, Gliding Vertex, ReDet;
——two-stage: DRN, DAL, R3Det, RSDet, S2A-Net
（3）针对场景文本检测（Scene text detection）
——RRPN：改进RPN，使用旋转的RPN生成旋转的边界框回归（generate rotated proposals and further perform rotated bounding box regression）
（4）回归损失目前都是基于边界框（bounding box）或点（point）或掩膜（mask-based）
——开始应用skewIoU，提出多种近似的SkewIoU Loss,解决其不可导的明显问题（R3Det,KFloss等）

2、基于IoU的LOSS函数领域：
（1）SCRDet：提出IOU-SmoothL1 loss函数，将IOU loss与Smooth L1 Loss相结合，部分（partly）避免（circumvents）梯度反向传播（gradient back propagation）对SkewIoU损失的需要；
（2）PolarMask: 提出Polar IoU loss，可以很大程度上简化优化，大大提高精度；
（3）基于像素（Pixel）的改进提出PIoU: 通过累积内部重叠像素的贡献，直接计算skewIoU;
（4）基于高斯的改进：包括GWD,KLD等，用高斯距离测量法模拟SkewIoU。

3、高斯分布建模的背景
首先介绍如何将任意方向的2D/3D边界框变换为高斯分布 G(μ, Σ) :

$$其中R表示旋转矩阵，\Lambda 表示特征值的对角矩阵。$$

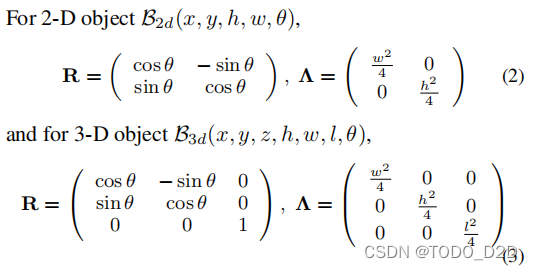
$$其中l,w,h分别表示三维边界框的长宽高。$$
值得注意的是，GWD属于基于高斯建模设计回归损失。与本文不同，GWD是直接用两个分布间的距离作为最后的损失。因为GWD不具备尺度不变性(因为高斯Wasserstein距离的第一项是中心点之间的欧氏距离)，为了保证模型训练的正常收敛性，需要通过非线性变换进行归一化。然而，这样的操作并不能保证模型训练的正常收敛。在本文中，作者从另外的角度来SkewIoU来更好地训练检测器，这更具有物理一致性。

四、具体工作

1、基于卡尔曼滤波的SkewIoU方法（SkewIoU based on Kalman Filtering）

图2展示了基于卡尔曼滤波器的SkewIoU在二维空间的近似过程。简要地，首先将边界框转换到为高斯分布，移动两个高维分布的中心点，使他们重合。然后，可以通过卡尔曼滤波获得重叠区域的分布函数。最后，将得到的分布函数转换为旋转边界框来计算重叠区域和IoU。

首先，当我们得到一个新的高斯分布时，我们可以很容易地根据它的协方差计算出对应旋转框的体积，其中 n 表示维数。

为了得到最终的SkewIoU，计算重叠面积是至关重要的。对于两个高斯分布，我们可以利用卡尔曼滤波器4来得到重叠区域的分布函数。具体公式如下：

其中α具体表示为：

其中：

可以观察到，Σ只与给定的两个高斯分布的协方差（Σ1和Σ2）有关，这意味着无论两个高斯分布如何移动，只要协方差是固定的，由公式(4)计算的区域是不会变的。这显然不符合直观的感受，当两个高斯分布都很远时，重叠的面积应该减小。主要原因是Gkf（μ，Σ）不是一个标准的高斯分布（概率和不是1），不能在不考虑 α 的情况下，通过公式(14)直接用 Σ 来计算重叠区域。从公式(6)可以发现，α与两个高斯分布的中心点之间的距离（μ1?μ2）有关。基于以上发现，z作者首先可以使用一个中心点损失Lc（μ1，μ2）来缩小两个高斯分布中心之间的距离，然后通过公式(14)得到的新位置计算重叠区域。这样，α就可以近似为一个常数，并介绍了可以很容易计算KFIoU损失：

其中B1、B2、B3为图2右侧所示的三个不同的边界框。

根据表1中的结果可以看到，相比之下，KFIoU的计算过程本质上是重叠率的计算，因此它不需要额外的超参数，并且可以与SkewIoU保持较高的趋势水平一致性。

结合三个数据集上的性能，较小的EVars往往具有更好的性能。因此，我们得出结论，保持度量损失和回归损失之间一致性的关键在于近似和精确的SkewIoU损失之间的趋势水平一致性，而不是值水平的一致性。基于高斯分布的损失(如KFIoU、KLD、GWD)优于普通SkewIoU损失的原因是由于先进的参数优化机制、对非重叠情况的有效测量和完整的推导。然而，超参数的引入使得KLD和GWD在Evar和性能方面不如KFIoU稳定。与利用分布距离近似SkewIoU的GWD和KLD相比，KFIoU在物理上比GWD和KLD更合理(符合SkewIoU的计算过程)，更简单，在经验上更有效。此外，KFIoU的实现比普通的SkewIoU要简单得多，并且可以很容易地通过现有的深度学习框架的操作来实现。

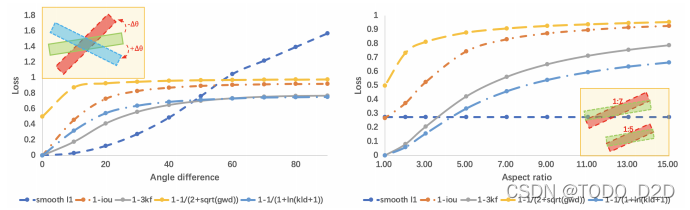
图3显示了具有同一个中心点的两个边界框在不同情形下三个损失函数的曲线。

需要注意的是，作者将KFIoU扩大了三倍，使得它的值域到 [0,1] 。情形1(左边)显示了角度差和损失函数之间的关系。尽管他们都具有单调性，但只有smooth L1曲线是凸的。情形2(右边)显示了是在不同长宽比下三个损失函数的变化。可以看到两个边界框的Smooth L1是常数(主要从角度差来看)，但是IoU损失和KFIoU损失会随着长宽比的变化而发生巨大的变化。无论哪种情形，KFIoU都可以和IoU保持相似的趋势。

2、KFIoU损失
为了符号简洁，本文以二维目标检测为例。本文采用一阶段的RetinaNet作为基准。用五个参数(x,y,w,h,θ)表示旋转框。首先，需要说明的是，网络并没有改变原来回归分支的输出，也就是说，它并没有直接预测高斯分布的参数。检测器的整个训练过程如下：
$$i)预测偏移(t_x^{?},t_y^{?},t_w^{?},t_h^{?},t_{\theta }^{?});ii)解码预测框；iii）将预测框和GT转换为高斯分布；iv)计算两个分布的L_c和L_k。$$
因此，推断时间保持不变。给出(x,y,w,h)的回归公式如下：

其中 x,y,w,h分别表示边界框的中心坐标，宽和高。变量X,Xa,X* 分别表示GT框，anchor和预测框(对y,w,h一样)。

对于θ的回归，作者采用两个形式作为基准进行计算：
$$(1)直接回归，记为Reg.(\Delta \theta )。模型直接预测角度偏移t_{\theta }^{?}:$$

$$(2)间接回归，记为Reg{.}^{?}(sin\theta ,cos\theta )。模型预测两个向量来匹配GT的两个目标：$$

间接回归是避免边界不连续问题的一种简单方法。

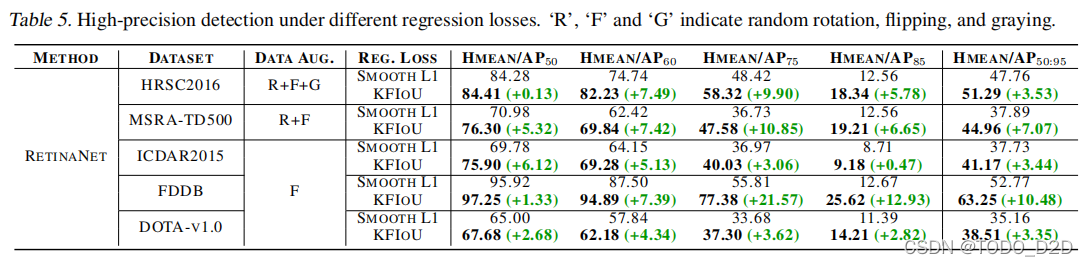
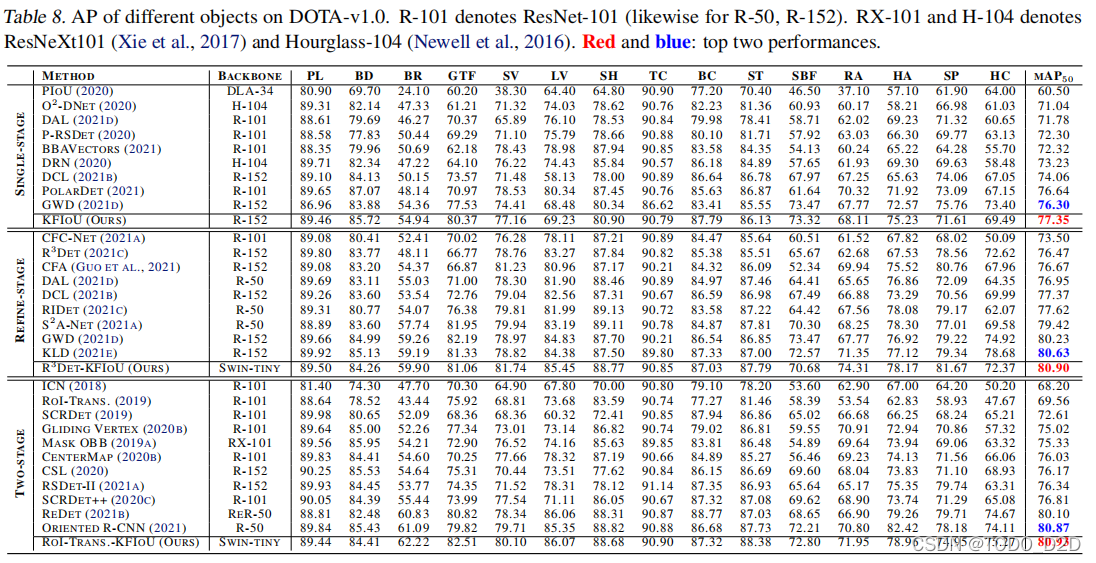
五、实验结果：

六、总结：

作者给出了一个近似于理想但梯度训练的SkewIoU损失的趋势水平，称之为KFIoU损失，因为采用卡尔曼滤波器直接模拟SkewIoU的计算机制。这种设计不同于基于分布距离的损失，包括GWD和KLD，它们在实现与SkewIoU损失的趋势水平对齐方面存在根本困难。此外，KFIoU比普通的SkewIoU更容易实现，因为它在非重叠情况下可以有效实现，且推导完整。在不同数据集上的二维和三维情况下的实验结果表明了该方法的有效性。

文章一开始介绍设计的算法损失可以大大解决长宽比和小目标的检测，但是从表中的指标来看，所提损失在small-vehicle和ship的指标上相比SOTA并不是最高。本文提出的方法，为旋转目标检测的进一步发展提供了新的思路，而且将相关技术推广到三维空间，为该领域开辟了新的方向。