无监督学习简介
无监督学习是一种机器学习的训练方式,它本质上是一个统计方法,在没有标签的数据里可以发现潜在的一些结构的一种训练方式。
无监督学习主要具备3个特点:
- 无监督学习没有明确的目的
- 无监督学习不需要给数据打标签
- 无监督学习无法量化效果
无监督学习的使用场景:
案例1:发现异常
有很多违法行为都需要”洗钱”,这些洗钱行为跟普通用户的行为是不一样的,到底哪里不一样?
如果通过人为去分析是一件成本很高很复杂的事情,我们可以通过这些行为的特征对用户进行分类,就更容易找到那些行为异常的用户,然后再深入分析他们的行为到底哪里不一样,是否属于违法洗钱的范畴。
通过无监督学习,我们可以快速把行为进行分类,虽然我们不知道这些分类意味着什么,但是通过这种分类,可以快速排出正常的用户,更有针对性的对异常行为进行深入分析。
案例2:用户细分
这个对于广告平台很有意义,我们不仅把用户按照性别、年龄、地理位置等维度进行用户细分,还可以通过用户行为对用户进行分类。
通过很多维度的用户细分,广告投放可以更有针对性,效果也会更好。
案例3:推荐系统
大家都听过”啤酒+尿不湿”的故事,这个故事就是根据用户的购买行为来推荐相关的商品的一个例子。
比如大家在淘宝、天猫、京东上逛的时候,总会根据你的浏览行为推荐一些相关的商品,有些商品就是无监督学习通过聚类来推荐出来的。系统会发现一些购买行为相似的用户,推荐这类用户最”喜欢”的商品。
K-均值聚类算法
核心思想
聚类是一种无监督的学习方法,它将相似的对象归到同一个簇中。K-均值聚类算法可以发现K个不同的簇,且每个簇的中心采用簇中所含值的均值计算而成。
簇识别:簇识别给出聚类结果的含义。假定有一些数据,现在将相似数据归到一起,簇识别会告诉我们这些簇到底都是什么。
工作流程:
- 随机确定k个初始点作为质心;
- 将数据集中的每个点分配到一个簇中(按照与质心的距离进行分配,每个簇中一个质心);
- 更新每个簇的质心为该簇中所有点的平均值;
- 重复2-3步直到数据点的簇分配节点不再发生改变;
代码实现:
import numpy as np
from numpy.linalg import norm
class Kmeans:
'''Implementing Kmeans algorithm.'''
def __init__(self, n_clusters, max_iter=100, random_state=123):
self.n_clusters = n_clusters
self.max_iter = max_iter
self.random_state = random_state
def initializ_centroids(self, X):
np.random.RandomState(self.random_state)
random_idx = np.random.permutation(X.shape[0])
centroids = X[random_idx[:self.n_clusters]]
return centroids
def compute_centroids(self, X, labels):
centroids = np.zeros((self.n_clusters, X.shape[1]))
for k in range(self.n_clusters):
centroids[k, :] = np.mean(X[labels == k, :], axis=0)
return centroids
def compute_distance(self, X, centroids):
distance = np.zeros((X.shape[0], self.n_clusters))
for k in range(self.n_clusters):
row_norm = norm(X - centroids[k, :], axis=1)
distance[:, k] = np.square(row_norm)
return distance
def find_closest_cluster(self, distance):
return np.argmin(distance, axis=1)
def compute_sse(self, X, labels, centroids):
distance = np.zeros(X.shape[0])
for k in range(self.n_clusters):
distance[labels == k] = norm(X[labels == k] - centroids[k], axis=1)
return np.sum(np.square(distance))
def fit(self, X):
self.centroids = self.initializ_centroids(X)
for i in range(self.max_iter):
old_centroids = self.centroids
distance = self.compute_distance(X, old_centroids)
self.labels = self.find_closest_cluster(distance)
self.centroids = self.compute_centroids(X, self.labels)
if np.all(old_centroids == self.centroids):
break
self.error = self.compute_sse(X, self.labels, self.centroids)
def predict(self, X):
distance = self.compute_distance(X, self.centroids)
return self.find_closest_cluster(distance)
from numpy import *
import time
import matplotlib.pyplot as plt
## step 1: load data
print "step 1: load data..."
dataSet = []
fileIn = open('E:/Python/Machine Learning in Action/testSet.txt')
for line in fileIn.readlines():
lineArr = line.strip().split('\t')
dataSet.append([float(lineArr[0]), float(lineArr[1])])
## step 2: clustering...
print "step 2: clustering..."
dataSet = mat(dataSet)
k = 4
centroids, clusterAssment = kmeans(dataSet, k)
## step 3: show the result
print "step 3: show the result..."
showCluster(dataSet, k, centroids, clusterAssment)
二分K-均值算法
为了克服K-均值算法收敛于局部最小值的问题,有人提出了二分K-均值算法,该算法的核心思想如下:
算法首先将所有点作为一个簇,然后将该簇一分为二。之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE(误差平方和)的值。不断重复上述划分过程直到得到用户指定的簇数目。因为对误差取了平方,因此更重视那些远离中心的点。
import time
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
def distEclud(vecA,vecB):
"""
计算两个向量的欧式距离
"""
return np.sqrt(np.sum(np.power(vecA-vecB,2)))
def randCent(dataSet,k):
"""
随机生成k个点作为质心,其中质心均在整个数据数据的边界之内
"""
n=dataSet.shape[1] # 获取数据的维度
centroids = np.mat(np.zeros((k,n)))
for j in range(n):
minJ = np.min(dataSet[:,j])
rangeJ = np.float(np.max(dataSet[:,j])-minJ)
centroids[:,j] = minJ+rangeJ*np.random.rand(k,1)
return centroids
def kMeans(dataSet,k,distMeas=distEclud, createCent=randCent):
"""
k-Means聚类算法,返回最终的k各质心和点的分配结果
"""
m = dataSet.shape[0] #获取样本数量
# 构建一个簇分配结果矩阵,共两列,第一列为样本所属的簇类值,第二列为样本到簇质心的误差
clusterAssment = np.mat(np.zeros((m,2)))
# 1. 初始化k个质心
centroids = createCent(dataSet,k)
clusterChanged = True
while clusterChanged:
clusterChanged = False
for i in range(m):
minDist = np.inf
minIndex = -1
# 2. 找出最近的质心
for j in range(k):
distJI = distMeas(centroids[j,:],dataSet[i,:])
if distJI < minDist:
minDist = distJI
minIndex = j
# 3. 更新每一行样本所属的簇
if clusterAssment[i,0] != minIndex:
clusterChanged = True
clusterAssment[i,:]=minIndex,minDist**2
print(centroids) # 打印质心
# 4. 更新质心
for cent in range(k):
ptsClust = dataSet[np.nonzero(clusterAssment[:,0].A==cent)[0]] # 获取给定簇的所有点
centroids[cent,:] = np.mean(ptsClust,axis=0) # 沿矩阵列的方向求均值
return centroids,clusterAssment
def biKmeans(dataSet, k, distMeas=distEclud):
"""
二分k-Means聚类算法,返回最终的k各质心和点的分配结果
"""
m = dataSet.shape[0]
clusterAssment = np.mat(np.zeros((m,2)))
# 创建初始簇质心
centroid0 = np.mean(dataSet,axis=0).tolist()[0]
centList = [centroid0]
# 计算每个点到质心的误差值
for j in range(m):
clusterAssment[j,1] = distMeas(np.mat(centroid0),dataSet[j,:])**2
while (len(centList) < k):
lowestSSE = np.inf
for i in range(len(centList)):
# 获取当前簇的所有数据
ptsInCurrCluster = dataSet[np.nonzero(clusterAssment[:,0].A == i)[0],:]
# 对该簇的数据进行K-Means聚类
centroidMat, splitClustAss = kMeans(ptsInCurrCluster,2,distMeas)
sseSplit = sum(splitClustAss[:,1]) # 该簇聚类后的sse
sseNotSplit = sum(clusterAssment[np.nonzero(clusterAssment[:,0].A != i)[0],1]) # 获取剩余收据集的sse
if (sseSplit + sseNotSplit) < lowestSSE:
bestCentToSplit = i
bestNewCents = centroidMat
bestClustAss = splitClustAss.copy()
lowestSSE = sseSplit + sseNotSplit
# 将簇编号0,1更新为划分簇和新加入簇的编号
bestClustAss[np.nonzero(bestClustAss[:,0].A == 1)[0],0]= len(centList)
bestClustAss[np.nonzero(bestClustAss[:,0].A == 0)[0],0]= bestCentToSplit
print("the bestCentToSplit is: ",bestCentToSplit)
print("the len of bestClustAss is: ",len(bestClustAss))
# 增加质心
centList[bestCentToSplit] = bestNewCents[0,:]
centList.append(bestNewCents[1,:])
# 更新簇的分配结果
clusterAssment[np.nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:] = bestClustAss
return centList, clusterAssment
def load_data_make_blobs():
"""
生成模拟数据
"""
from sklearn.datasets import make_blobs # 导入产生模拟数据的方法
k = 5 # 给定聚类数量
X, Y = make_blobs(n_samples=1000, n_features=2, centers=k, random_state=1)
return X,k
if __name__ == '__main__':
X, k=load_data_make_blobs() # 获取模拟数据和聚类数量
s = time.time()
myCentroids, clustAssing = biKmeans(X, k) # myCentroids为簇质心
print("用二分K-Means算法原理聚类耗时:", time.time() - s)
centroids = np.array([i.A.tolist()[0] for i in myCentroids]) # 将matrix转换为ndarray类型
# 获取聚类后的样本所属的簇值,将matrix转换为ndarray
y_kmeans = clustAssing[:, 0].A[:, 0]
# 未聚类前的数据分布
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.title("未聚类前的数据分布")
plt.subplots_adjust(wspace=0.5)
plt.subplot(122)
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', s=100, alpha=0.5)
plt.title("用二分K-Means算法原理聚类的效果")
plt.show()
K-means聚类实战
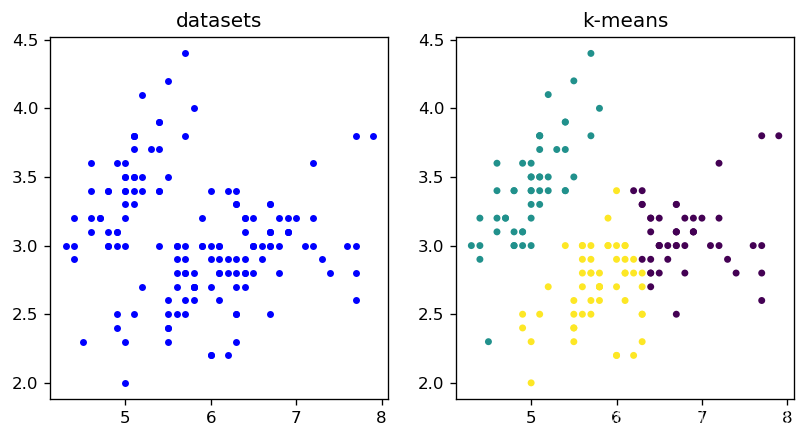
鸢尾花分类
from sklearn import datasets
iris = datasets.load_iris() #返回鸢尾花数据集
x = iris.data[:, 0:2] #共四个特征,选取前两个特征;
print(x.shape) #150个样本(行),2个特征(列)
#训练模型
from sklearn.cluster import KMeans
clusters = 3 #聚成3个类别
#verbose=1,输出迭代过程信息;迭代次数不超过100次;当新簇中心和旧簇中心的误差小于0.01,退出迭代;进行3次k-means,选取效果最好的一次
model = KMeans(n_clusters=clusters,verbose=1,max_iter=100,tol=0.01,n_init=3) #构造模型
model.fit(x) #训练数据
#获得各种指标
y_predict = model.labels_ #获取聚类标签,从0开始
centers = model.cluster_centers_ #聚类的中心点
distance = model.inertia_ #每个点到其簇的质心的距离平方的和
iterations = model.n_iter_ #总迭代次数,不会超过参数max_iter
print("centers = " , centers)
print("distance = ", distance)
print("iterations = ", iterations)
#对比数据集与聚类效果
import matplotlib.pyplot as plt
plt.figure(figsize=(8,4),dpi=120) #画布的宽是8英寸,高是4英寸;每英寸有120个像素
#(1)绘制原数据集
plt.subplot(1,2,1) #画布分为1行,2列,共2格,当前绘图区设定为第1格
plt.scatter(x[:, 0], x[:, 1], c = "blue", marker='o',s=10) #形状是圆圈;圆圈大小是10;颜色是蓝色
plt.title("datasets") #标题是"datasets"
#(2)绘制k-means结果
plt.subplot(1,2,2) #当前绘图区设定为第2格
plt.scatter(x[:, 0], x[:, 1], c = y_predict, marker='o',s=10) #不同类别不同颜色
plt.title("k-means")
#(3)显示
plt.show()