[人工智能]机器学习QAQ

泛化能力：学得模型适用于新样本的能力。

通常假设样本空间中全体样本服从一个未知“分布”D，我们获得的每个样本都是独立地从这个分布上采样获得的，即“独立同分布”。

归纳偏好：机器学习算法在学习过程中对某种类型假设的偏好。
任何一个有效的机器学习算法必有其归纳偏好，否则将被假设空间中看似在训练集上“等效”的假设所迷惑，而无法产生确定的学习结果。

一般性原则引导算法确立“正确”偏好：
“奥卡姆剃刀”：若有多个假设与观察一致，则选最简单那个。

没有免费午餐（NFL） 定理：
总误差与学习算法无关，对于任意两个学习算法 Ea 和 Eb，我们都有

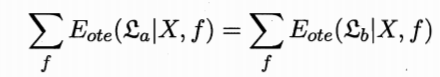
也就是说，无论学习算法 Ea 多聪明、Eb 多笨拙，它们的期望性相同。

脱离具体问题空泛谈论“什么学习算法更好”毫无意义，因为若考虑所有潜在问题，则所有学习算法一样好。

错误率：分类错误的样本数占样本总数的比例。E = a / m（ m 个样本中有 a 个样本分类错误）
精度：1 - a / m
误差：学习器的实际预测输出与样本的真实输出之间的差异。
训练误差(经验误差)：学习器在训练集上的误差。
泛化误差：学习器在新样本上的误差。

过拟合：学习器把训练样本学得太“好”，很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，导致泛化性能下降。
欠拟合：学习器对训练样本的一般性质尚未学好。（易克服）

过拟合是机器学习面临的关键障碍，无法彻底避免，只能“缓解”，或者说减小其风险。
机器学习面临的问题通常是 NP 难甚至更难，而有效的学习算法必然是在多项式时间内运行完成，若可彻底避免过拟合，则通过经验误差最小化就能获得最优解，也就意味构造性证明“P = NP”。

评估方法

通过实验测试来对学习器的泛化误差进行评估并进而做出选择，为此，需使用一个“测试集”来测试学习器对新样本的判别能力，然后以测试集上的“测试误差”作为泛化误差的近似。
假设测试样本也是从样本真实分布中独立同分布采样而得，但测试集应该尽可能与训练集互斥，即测试样本尽量不在训练集中出现、未在训练过程中使用过。

一个包含 m 个样例的数据集 D = {(x1, y1), (x2, y2), ……, (xm, ym)}，通过对 D 进行适当处理，从中产生训练集 S 和测试集 T。

• 留出法：直接将数据集 D 划分为两个互斥集合，其中一个作为 S ，另一个作为 T，即 D = S ∪ T， S ∩ T = ?，在 S 上训练出模型后，用 T 来评估其测量误差，作为对泛化误差的估计。
  单次使用留出法得到的估计结果往往不够稳定可靠，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
  常用做法：将大约 2/3 ~ 4/5 的样本用于训练，剩余样本用于测试。
• 交叉验证法( k 折交叉验证)：将数据集 D 划分为 k 个大小相似的互斥子集，即 D = D1 ∪ D2 ∪ …… ∪ Dk，Di ∩ Dj = ?（i != j），每个子集 Di 都尽可能保持数据分布的一致性，即从 D 中通过分层采样得到。然后，每次用 k - 1 个子集的并集作为训练集，余下的那个子集作为测试集。这样可获 k 组训练/测试集，从而可进行 k 次训练和测试，最终返回这 k 个测试结果的均值。
  稳定性和保真性很大程度取决于 k 的取值。k 常用取值为10，其他常用有5、20等。
  假定数据集 D 中包含 m 个样本，若令 k = m，则得到特例：留一法。
  该法不受随机样本划分方式的影响，评估结果往往被认为比较准确。
  缺陷：在数据集比较大时，训练 m 个模型的计算开销难以忍受，且估计结果未必永远比其他评估方法准确。
• 自助法：以自助采样为基础，给定 m 个样本的数据集 D，对它采用产生数据集 D’：每次随机从 D 中挑选一个样本，将其拷贝放入 D’，然后再将该样本放回初始数据集 D 中，使得该样本在下次采样时仍有可能被采到，重复执行 m 次。
  显然，D 中有一部分样本会在 D’ 中多次出现，而另一部分样本不出现，可以做一个简单的估计，样本在 m 次采样中
  
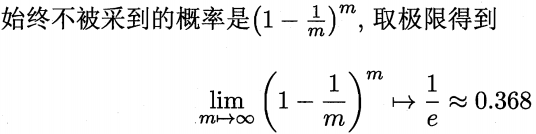
  即通过自助采样，初始数据集 D 中约有 36.8% 的样本未出现在采样数据集 D’ 中，于是可将 D’ 用作训练集，D\D’ （‘\’表示集合减法）用作测试集。
  实际评估的模型与期望评估的模型都使用 m 个训练样本，而仍有数据总量约 1/3 的、没在训练集中出现的样本用于测试，这样的测试结果称“包外估计”。
  在数据集较小、难以有划分训练/测试集时很有用。此外，自助法能从初始数据集中产生多个不同的训练集，对集成学习等方法有很大好处。
  然而，自助法产生的数据集改变了初始数据集的分布，会引入估计偏差，因此，在初始数据量足够时，留出法和交叉验证法更常用。

调参与最终模型

给定包含 m 个样本的数据集 D，在模型评估与选择过程中由于需要留出一部分数据进行评估测试，事实上我们只使用了一部分数据训练模型。因此在模型选择完成后，学习算法和参数配置已选定，此时应该用数据集 D 重新训练模型，这个模型在训练过程中使用了所有 m 个样本，是最终提交给用户的模型。

测试数据：学得模型在实际使用中遇到的数据。
验证集：模型评估与选择中用于评估测试的数据集。

性能度量

对于数据集 D ，分类




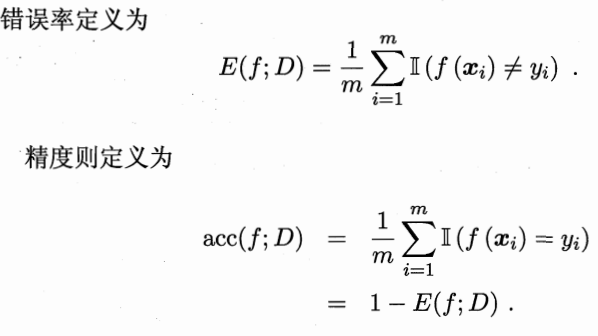
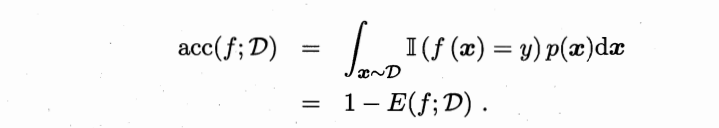
查准率和查全率是一队矛盾的度量，一般来说，查准率高时，查全率往往偏低，查全率高时，查准率往往偏低。

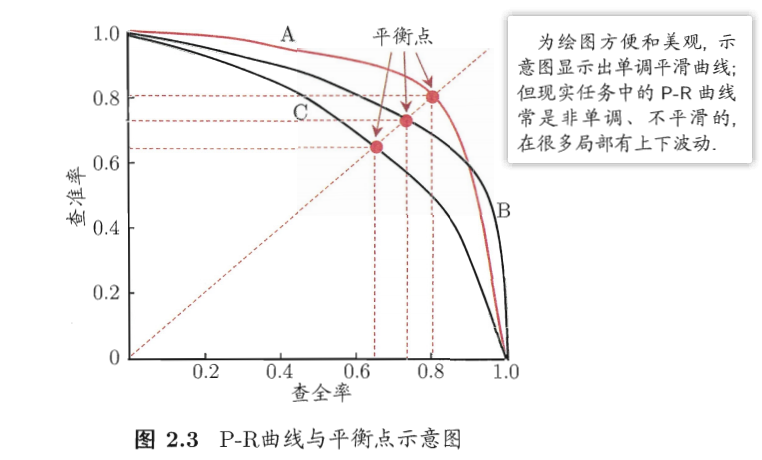
在进行比较时，若一个学习器的 P - R 曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者。如果发生交叉，则难断孰优孰劣，只能在具体的查准率或查全率条件下进行比较。

平衡点(BEP)：查准率 = 查全率 时的取值。
BEP过于简化，更常用的是 F1 度量：

F1 度量的一般形式能让我们表达出对查准率/查全率的不同偏好，定义为：

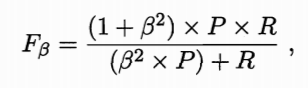
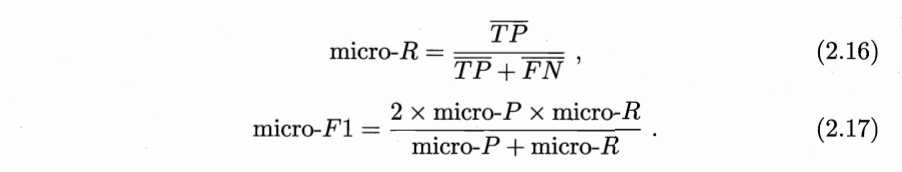
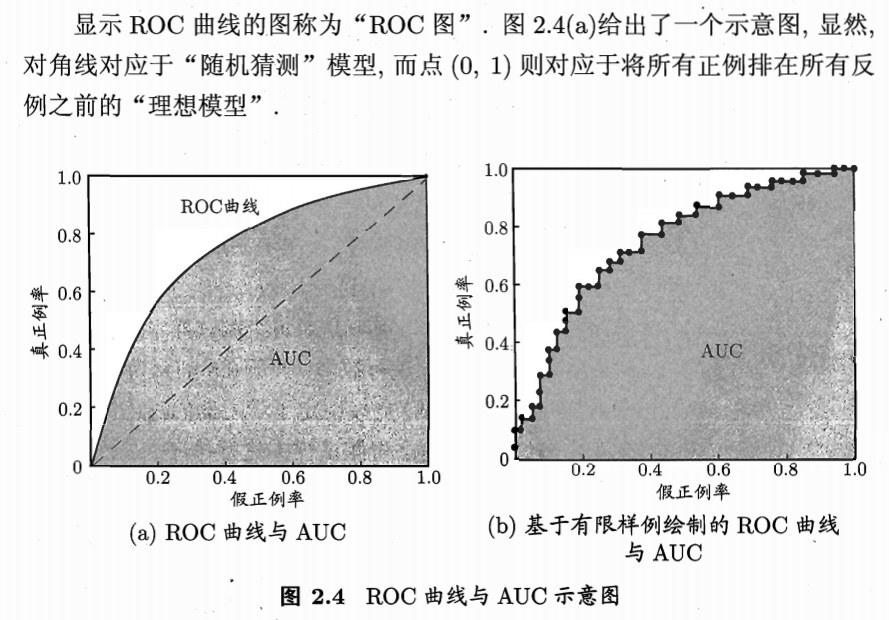
受试者工作特征（ROC）：根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，得到“ROC曲线”。纵轴“真正例率(TPR)”，横轴“假正例率(FPR)”。

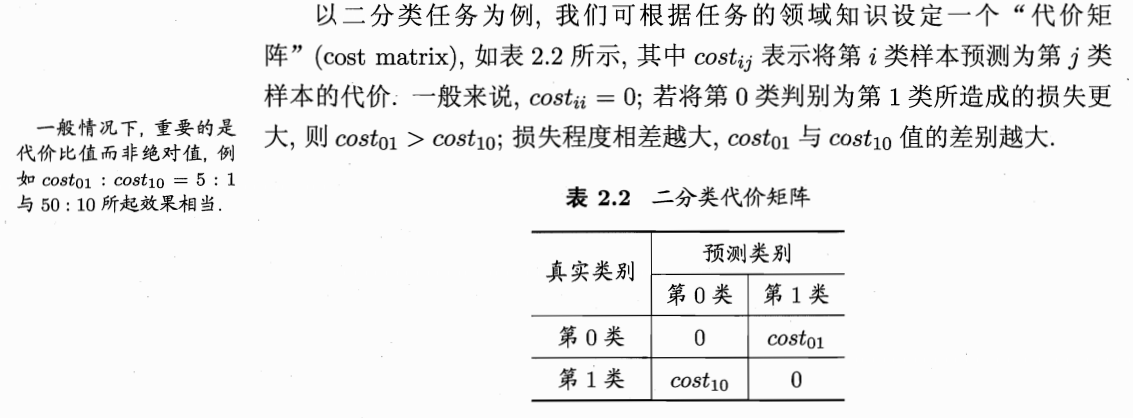
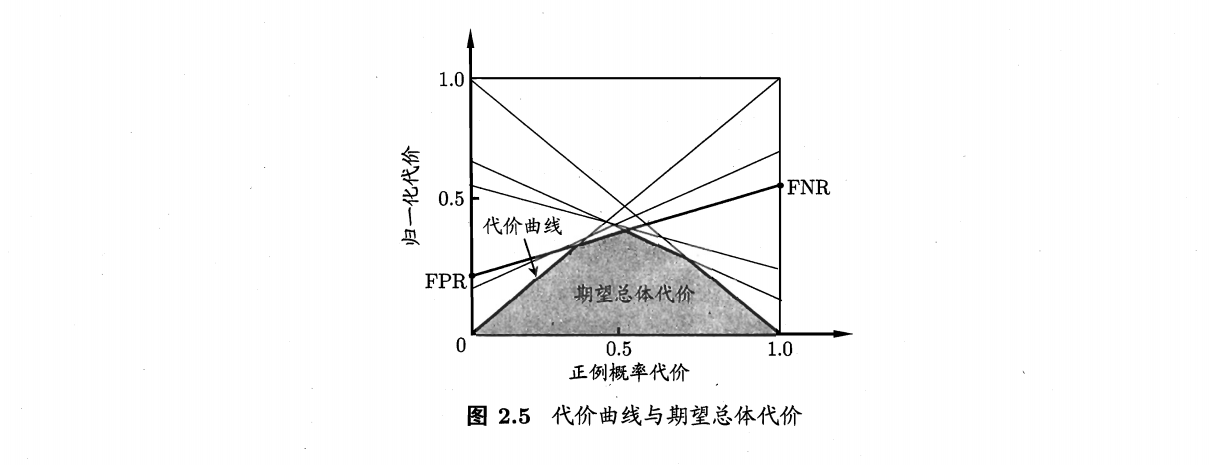
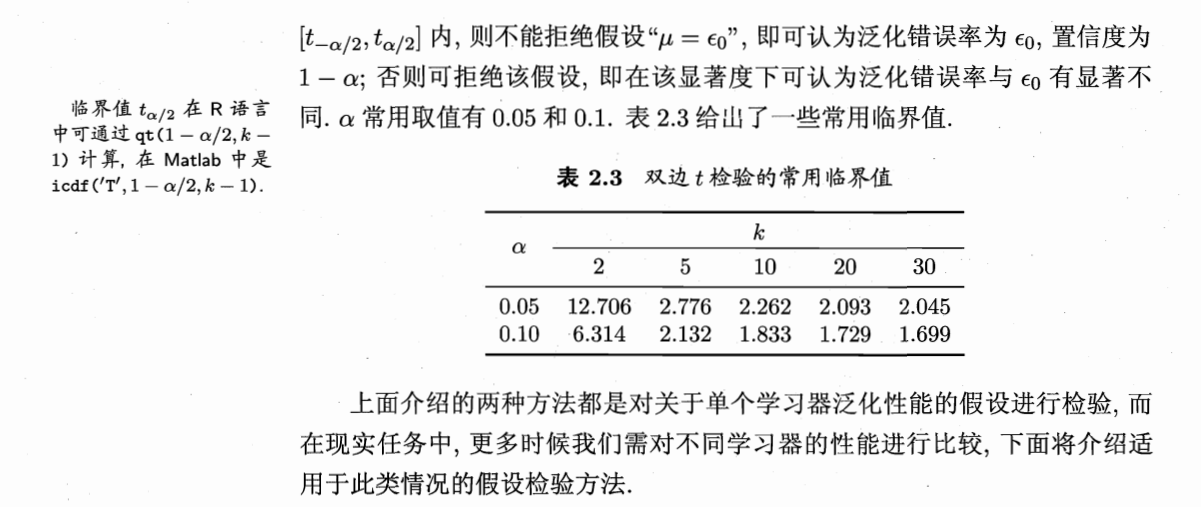
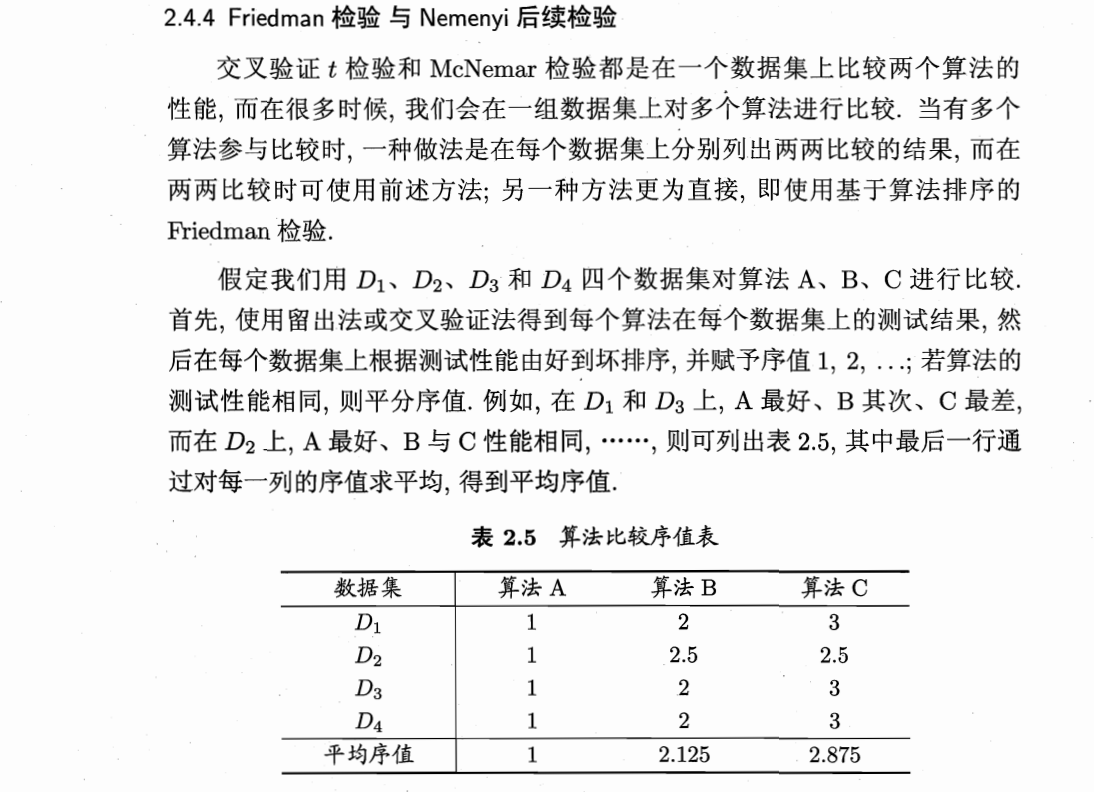
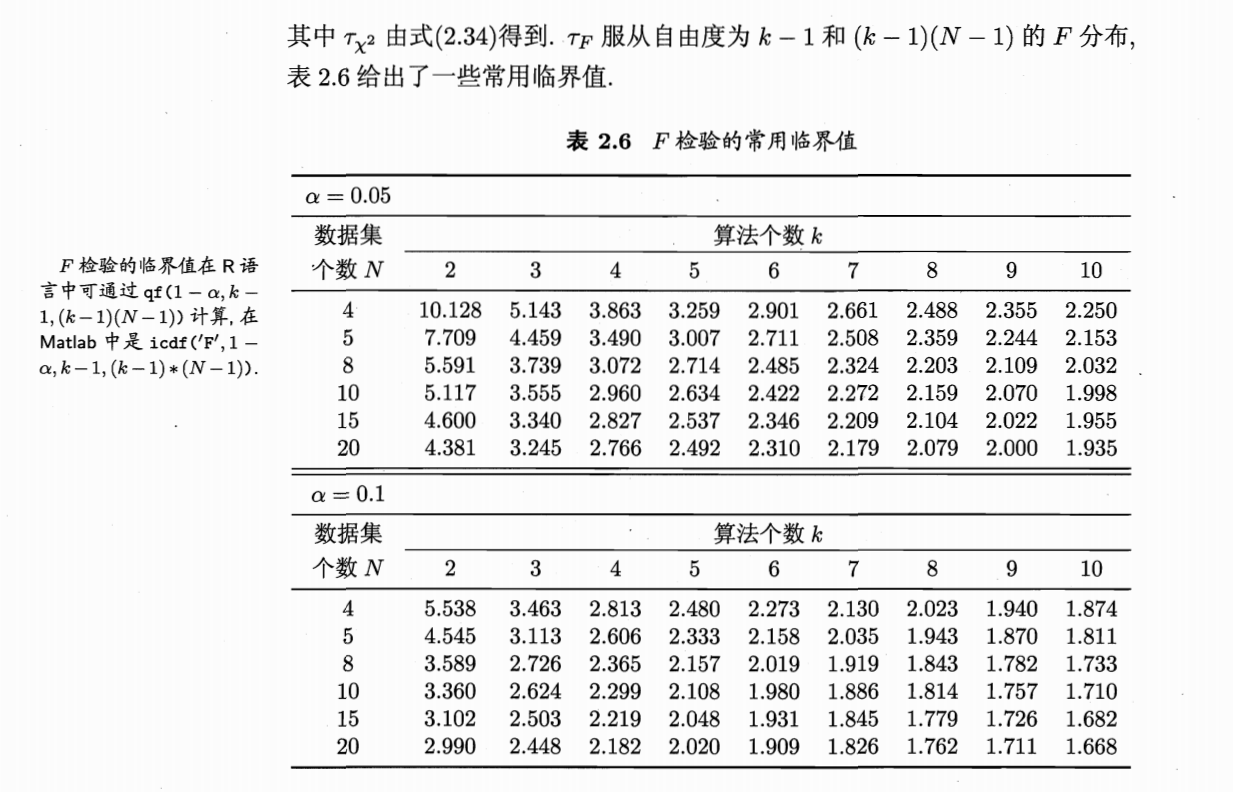
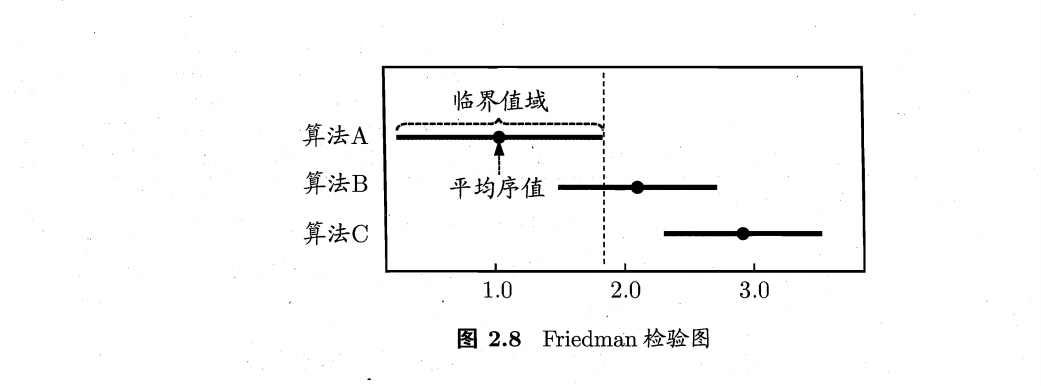
比较检验：

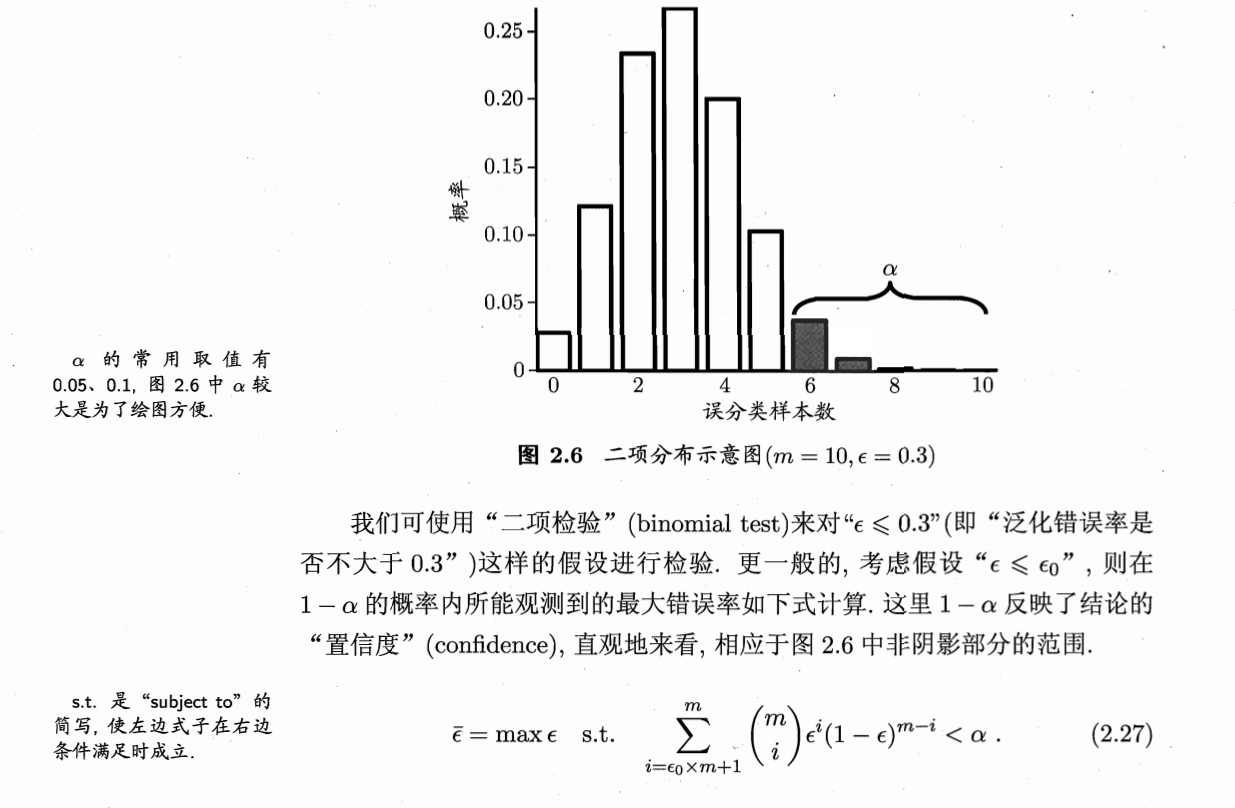
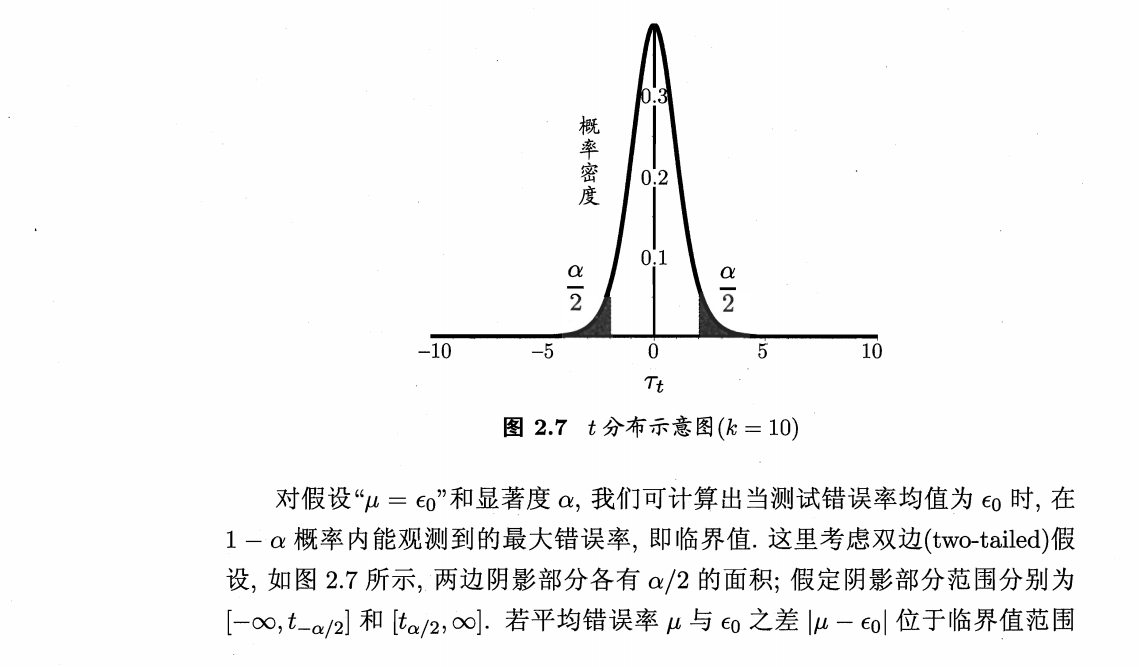
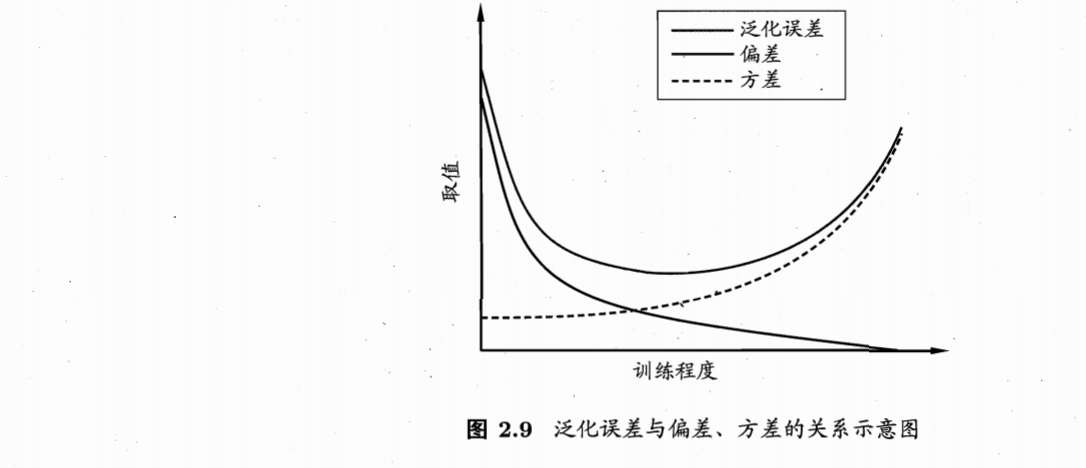
偏差与方差

K-近邻算法

# _*_coding:utf-8_*_

from numpy import *
import operator


def createDataSet():
    group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
    labels = ['A', 'A', 'B', 'B']
    return group, labels


def classify0(inX, dataSet, labels, k): # labels 的元素数目和矩阵 dataSet 的行数相同
    '''
    :param inX: Input vectors for classification
    :param dataSet: Input training sample set
    :param labels:  Label vectors
    :param k:   Number of nearest neighbours for selection
    :return:    Return the category with the highest frequency in the first k points as the predicted classification for the current point
    '''
    # 计算已知类别数据集中的点与当前点之间的欧式距离
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet
    sqDiffMat = diffMat ** 2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5

    sortedDistIndicies = distances.argsort()    # 按照距离递增次序排序
    classCount = {}
    for i in range(k):  # 选取距离最小的 k 个点
        voteIlabel = labels[sortedDistIndicies[i]]  # 分类
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1  # 确定前 k 个点所在类别的出现频率
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) # 按照出现频率递减排序
    return sortedClassCount[0][0]

def file2matrix(filename):  # 文本记录转换NumPy的解析
    fr = open(filename)
    arrayOLines = fr.readlines()
    numberOfLines = len(arrayOLines)    # 得到的文件行数
    returnMat = zeros((numberOfLines, 3))   # 创建返回的 NumPy矩阵
    classLabelVector = []
    index = 0

    # 解析文件数据到列表
    for line in arrayOLines:
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3]
        classLabelVector.append(int(listFromLine[-1]))
        index += 1
    return returnMat, classLabelVector


datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
'''
import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:, 1], datingDataMat[:, 2], 15.0 * array(datingLabels), 15.0 * array(datingLabels))
plt.show()
'''

# newValue = (oldValue - min) / (max - min) 可以将任意取值范围的特征之转化为 0 到 1 区间内的值 （归一化）
def autoNorm(dataSet):
    minVals = dataSet.min(0)    # 最小特征值，参数 0 使得函数可以从列中选取最小值
    maxVals = dataSet.max(0)    # 最大特征值
    ranges = maxVals - minVals  # 计算可能的取值范围
    m = dataSet.shape[0]    # 创建新的返回矩阵
    normDataSet = dataSet - tile(minVals, (m, 1))   # tile() 函数将变量内容复制成输入矩阵同样大小的矩阵
    normDataSet = normDataSet / tile(ranges, (m, 1))    # 这是具体特征值相除。（对于某些数值处理软件包，’/‘可能意味着矩阵除法，但在NumPy库中，矩阵除法需要使用函数 linalg.solve(matA, matB) ）
    return normDataSet, ranges, minVals

normMat, ranges, minVals = autoNorm(datingDataMat)
print(normMat)
print(ranges)
print(minVals)

决策树

监督学习。
描述对数据进行分类的树形模型，可以是二叉树或非二叉树。
内部结点(绿)表示一个特征或属性，叶子结点(橘)表示一个结果类。

能用来做回归(叶子结点值指代输出值)、分类

常见决策树算法：ID3，C4.5，C5.0，CART(分类效果一般优于其他决策树)

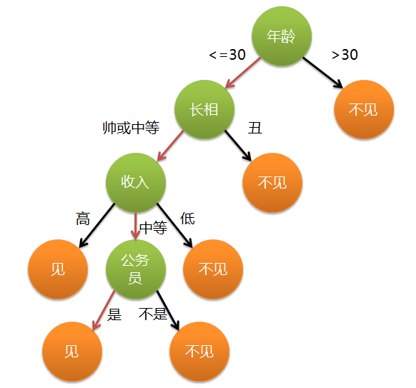
ID3算法

根据 信息增益(熵减) 来选择进行划分的特征，然后递归地构建决策树。
适用于离散型数据。

信息量：对信息的度量。
越小概率的事情发生产生的信息量越大，越大概率的事情发生产生的信息量越小。
一个具体事件的信息量随着其发生概率而递减，且不能为负。

如果有两个不相关的事件 x 和 y，那么观察到的两个事件同时发生时获得的信息等于各自发生时获得的信息之和，即h(x, y) = h(x) + h(y)。
由于不相关，满足p(x, y) = p(x) * p(y)。
易得h(x)和p(x)的对数相关。
信息量的定义是概率倒数（为了使概率越大，信息量越小，并且因为概率的倒数大于1，其对数自然大于0）的对数。
故推知：h(x) = $?lo{g}_2$p(x)

信息熵：信息量度量是一个具体事件发生所带来的信息，而熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。

信息熵公式：
（表征信息不确定性的程度，分类属性应当以最高熵减为标准进行）

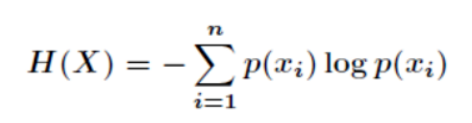
步骤：

1. 从根结点开始，计算所有可能特征的信息增益，选择信息增益最大的特征作为结点划分特征。
2. 由该特征的不同取值建立子结点。
3. 对子结点递归1~2步，构建决策树。
4. 直到没有特征可以选择或类别完全相同为止，得到最终的决策树。

优点：

• 计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。

缺点：

• 没有剪枝，可能会产生过度匹配问题，所以需要进行剪枝。
• 采用信息增益作为选择最优划分特征的标准，但是信息增益会偏向那些取值较多的特征。

C4.5算法

ID3算法的一种延伸和优化。

改进点：

1. 用信息增益率来选择划分特征，克服了用信息增益选择的不足，但信息增益率对可取值数目较少的属性有所偏好。
2. 能够处理离散型和连续型的属性类型，即将连续型的属性进行离散化处理。
3. 能够处理具有缺失属性值的训练数据。
4. 在构造树的过程中进行剪枝。

特征选择(选择最优划分属性)：从当前数据特征中选择一个特征作为当前结点的划分标准，随着划分过程不断进行，希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点“纯度”越来越高。

信息增益率公式：
A = [a1, a2, ……, ak]。
若使用 A 对样本集 D 进行划分，则会产生 k 个分支结点，其中第 k 个结点包含 D 中所有属性 A 上取值为 ak 的样本，记为 Dk。
通常，属性 A 的可能取值数越多(即 k 越大)，则 IV(A) 的值越大。

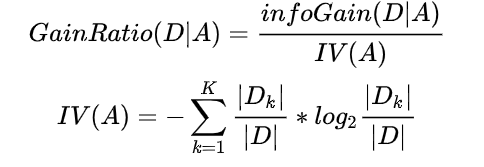
信息增益率准则对可取值数目较少的属性有所偏好。
所以，C4.5算法不是直接选择信息增益率最大的候选划分属性，而是先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的。

对连续特征的处理：

1. m个样本的连续特征 A 有 m 个值，从小到大排列 a1, a2, ……, am，取相邻两样本值的平均数做划分点，一共有 m - 1 个，其中第 i 个划分点 Ti 表示为：$T_i=（a_i+a_{i+1}）$/ 2。
2. 分别计算以这 m - 1 个点作为二元切分点时的信息增益率。选择信息增益率最大的点为该连续特征的最佳切分点。比如取到的信息增益率最大的点为 $a_t$，则小于 $a_t$ 的值为类别 1，大于 $a_t$ 的值为类别2，这样就做到了连续特征的离散化。

对缺失值的处理：

• 根据缺失比例，折算信息增益（无缺失值样本所占的比例 * 无缺失值样本子集的信息增益）和信息增益率。
• 将样本以不同概率同时划分到不同结点中，概率是根据其他非缺失属性的比例来得到的。
• 走所有分支，计算每个类别的概率，取概率最大的类别赋值给该样本。

剪枝：（过拟合的树在泛化能力的表现非常差）

前剪枝：（在构造树的过程中就知道哪些 结点可以剪掉）

在结点划分前确定是否继续增长，及早停止增长的主要方法：

• 结点内数据样本数小于切分最小样本数阈值
• 所有结点特征都已分裂
• 结点划分前准确率比划分后高

优点：降低过拟合风险，减少训练时间
缺点：基于“贪心”策略，会带来欠拟合风险。

后剪枝：（在已经生成的决策树上进行剪枝，得到简化版的剪枝决策树）

C4.5算法采用悲观剪枝方法。
根据剪枝前后的误判率来判定是否进行子树的修剪。
如果剪枝后与剪枝前相比其误判率是保持或者下降，则这棵子树就可以被替换为一个叶子结点。因此，不需要单独的剪枝数据集。C4.5通过训练数据集上的错误分类数量来估算未知样本上的错误率。

把一棵子树（具有多个叶子结点）的剪枝后用一个叶子结点来替代的话，在训练集上的误判率肯定是上升的，但在新数据上不一定。于是我们需要把子树的误判计算加上一个经验性的惩罚因子。
对于一棵叶子结点，它覆盖了 N 个样本，其中有 E 个错误，那么该叶子结点的错误率为（E + 0.5）/ N。
0.5为惩罚因子。
那么一棵子树，有 L 个叶子结点，那么该子树的误判率估计为：

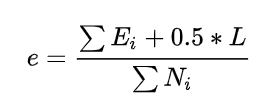
其中，Ei 表示子树的每一个叶子结点的误判样本数量，L 为子树的叶子结点个数，Ni 为每一个叶子结点的样本数量。

如此，一棵子树虽然具有多个子结点，但由于加上了惩罚因子，所以子树的误判率计算未必占到便宜。剪枝后内部结点变成了叶子结点，其误判个数 J 也需要加上一个惩罚因子，变成 J + 0.5。
那么子树是否可以被剪枝就取决于剪枝后的错误 J + 0.5 是否在（sum（Ei）+ 0.5 * L）的标准误差内。
对于样本的误判率 e，可以根据经验把它估计成各种各样的分布模型，比如二项式分布、正态分布等。

那么一棵树错误分类一个样本值为1，正确分类一个样本值为0，该树错误分类的概率(误判率)为 e。

树的误判次数是伯努利分布，可以估计出该树的误判次数的均值和标准差：

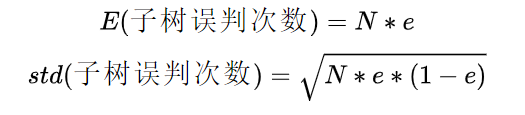
把子树替换成叶子结点后，该叶子的误判次数也是一个伯努利分布，因为子树合并为一个叶子结点了，所以 L = 1，将其代入上面计算误判率的公式中，可以得到叶子结点的误判率为

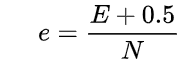
因此叶子结点的误判次数均值为

这里采用一种保守的分裂方案，即有足够大的置信度保证分裂后准确率比不分裂时的准确率高时才分裂，否则就不分裂——也就是应该剪枝。

如果要分裂(即不剪枝)至少要保证分裂后的误判数 E (子树误判次数) 要小于不分裂的误判数 E (叶子结点的误判次数)，而且为了保证足够高的置信度，加了一个标准差可以有 95% 的置信度，所以，要分裂(即不剪枝)需满足如下不等式：

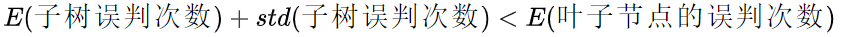
反之则不分裂(即剪枝)。

优点：

• 产生的分类规则易于理解，准确率较高。

缺点：

• 只能用于分类
• 是多叉树，用二叉树效率会提高
• 在构造树的过程中，需要对数据集进行多次的顺序扫描和排序(尤其是对连续特征)，因而导致算法的低效
• 在选择分裂属性时没有考虑到条件属性间的相关性，只计算数据集中每一个条件属性与决策属性之间的期望信息，有可能影响到属性选择的正确性。
• 只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行

检测数据集中的每一个子项是否属于同一分类：
    if so return 类标签；
    else
        寻找划分数据集的最好特征
        划分数据集
        创建分支节点
            for 每个划分的子集
                调用函数 createBranch 并增加返回结果到分支节点中
        return 分支节点

随机森林

一种由决策树构成的集成算法，不同决策树之间没有关联。
属于集成学习中的 Bagging（Bootstrap AGgregation） 方法。

当我们进行分类任务时，新的输入样本进入，就让森林中的每一棵决策树分别进行判断和分类，每个决策树会得到一个自己的分类结果，决策树的分类结果中哪一个分类最多，那么随机森林就会把这个结果当做最终的结果。

Logistic 回归

每个回归系数初始化为1
重复 R 次：
    计算整个数据集的梯度
    使用 alpha * gradient 更新回归系数的向量
    返回回归系数

# _*_coding:utf-8_*_

import numpy as np

def loadDataSet():  # 读取数据

    dataMat = []
    labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # x0=1.0,x1,x2
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat

def sigmoid(inX):   # sigmoid 函数
    return 1.0/(1+np.exp(-inX))

def gradAscent(dataMatIn, classLabels): # 梯度上升算法
    # :param dataMatIn: 2维数组，每列分别代表每个不同的特征，每行代表每个训练样本
    # :param classLabels: 类别标签

    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose() # 行向量转置成列向量
    m,n = np.shape(dataMatrix)
    alpha = 0.001 # 步长
    maxCycles = 500 # 迭代次数
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights

def plotBestFit(wei):   # 画出数据集和 Logistic 回归最佳拟合直线的函数

    import  matplotlib.pyplot as plt
    weights = wei.getA()
    # weights = wei
    dataMat, labelMat = loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1])
            ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1])
            ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0] - weights[1] * x)/weights[2]
    ax.plot(x,y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
print(weights)  # [[ 4.12414349] [ 0.48007329] [-0.6168482 ]]
plotBestFit(weights)

def stocGradAscent0(dataMatrix, classLabels):   # 随机梯度上升算法
    m,n = np.shape(dataMatrix)
    alpha = 0.01
    weights = np.ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

dataArr,labelMat = loadDataSet()
weights2 = stocGradAscent0(np.array(dataArr),labelMat)
print('weights2:',weights2) #  [ 1.01702007  0.85914348 -0.36579921]
plotBestFit(weights2)

def stocGradAscent1(dataMatrix, classLabels, numIter=150):  # 改进的随机梯度上升算法
    m,n = np.shape(dataMatrix)
    weights = np.ones(n)
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01 # alpha 每次迭代时需要调整
            randIndex = int(np.random.uniform(0,len(dataIndex))) # 随机选取更新
            h = sigmoid(sum(dataMatrix[i]*weights))
            error = classLabels[i] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

def classifyVector(inX, weights):   # 根据 Sigmoid 值判断分类
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5:return 1.0
    else: return 0.0

def colicTest():    # 打开训练集和测试集，并对数据进行格式化处理，以及训练、测试
    frTrain = open('horseColicTraining.txt')
    frTest = open('horseColicTest.txt')
    trainingSet = []
    trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 500)
    errorCount = 0
    numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(np.array(lineArr), trainWeights)) != int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)
    print('the error rate of this test is : %f' % errorRate)
    return errorRate

def multiTest():    # 重复测试，并求取平均值

    numTests = 10
    errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print('after %d iterations the average error rate is : %f' % (numTests, errorSum/float(numTests)))

multiTest()