[人工智能]SOM自组织（竞争型）神经网络（Python实现）

SOM是神经网络的一种，它可以将相互关系复杂且非线性的高维数据，映射到具有简单几何结构及相互关系的低维空间中进行展示。（低维映射能够反映高维特征之间的拓扑结构）

可以实现数据的可视化；聚类；分类；特征抽取等任务。（主要做数据可视化）

网络结构

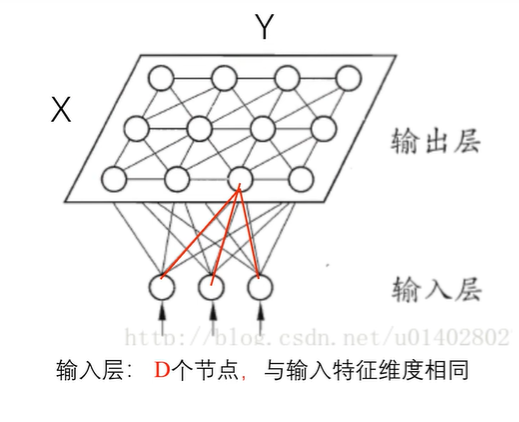
相关解释

?

模型训练过程

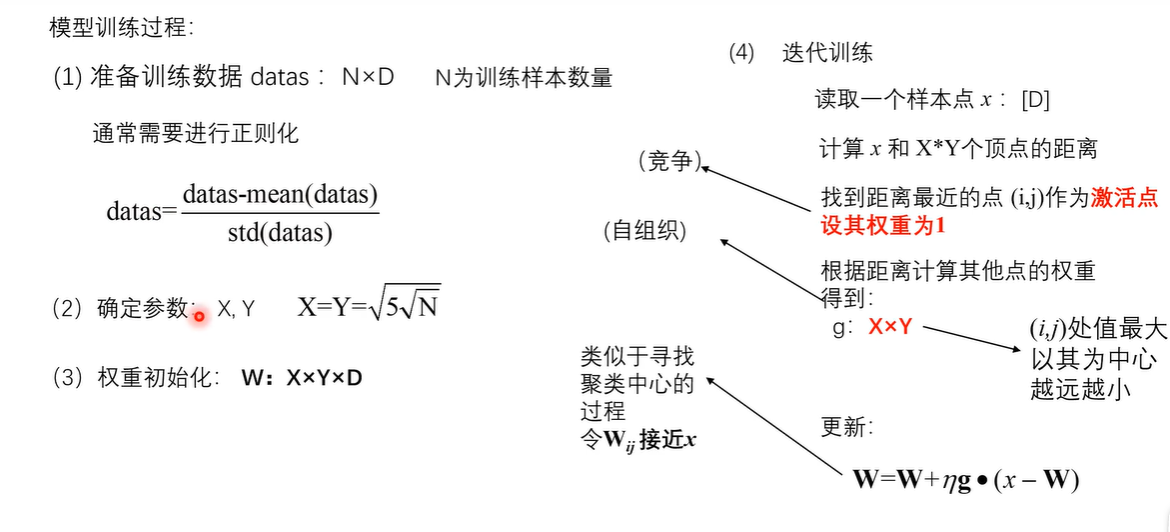
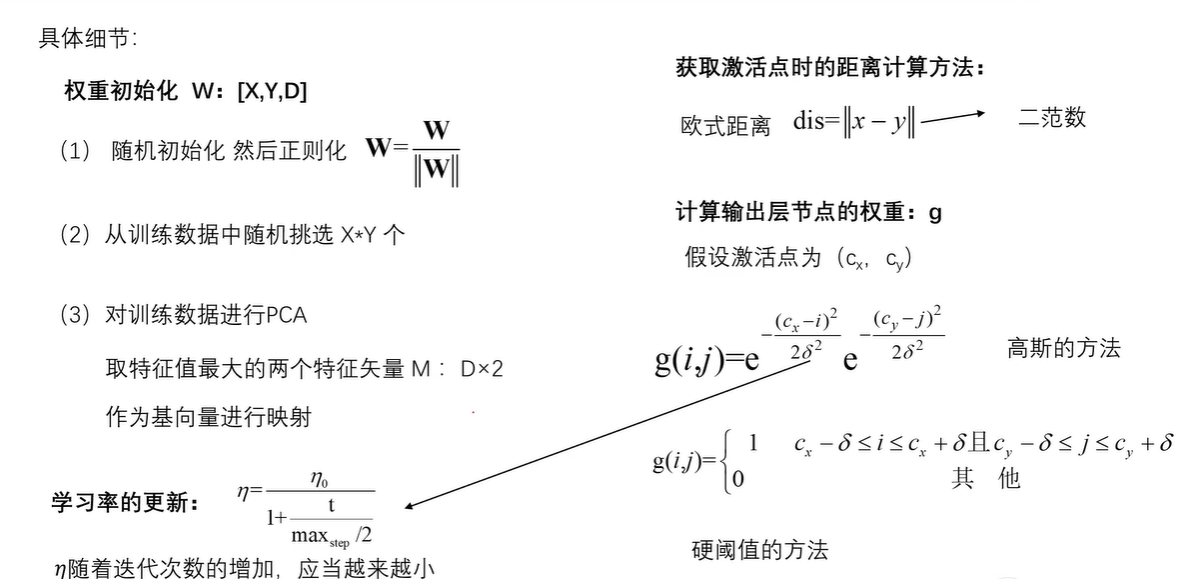
具体细节

代码实现

seeds_dataset数据集

链接: https://pan.baidu.com/s/1QYU70IGu8XEtHGDmm29KlA?pwd=yame 提取码: yame 复制这段内容后打开百度网盘手机App，操作更方便哦

训练模型

import numpy as np
import random
import tqdm
import matplotlib.pyplot as plt
import pandas as pd


# 利用高斯距离法计算临近点的权重
# X,Y 模板大小，c 中心点的位置， sigma 影响半径
def gaussion_neighborhood(X, Y, c, sigma):
    xx, yy = np.meshgrid(np.arange(X), np.arange(Y))
    d = 2 * sigma * sigma
    ax = np.exp(-np.power(xx - xx.T[c], 2) / d)
    ay = np.exp(-np.power(yy - yy.T[c], 2) / d)
    return (ax * ay).T


# 利用bubble距离法计算临近点的权重
# X,Y 模板大小，c 中心点的位置， sigma 影响半径
def bubble_neighborhood(X, Y, c, sigma):
    neigx = np.arange(X)
    neigY = np.arange(Y)

    ax = np.logical_and(neigx > c[0] - sigma,
                        neigx < c[0] + sigma)
    ay = np.logical_and(neigy > c[1] - sigma,
                        neigy < c[1] + sigma)
    return np.outer(ax, ay) * 1.


# 计算学习率
def get_learning_rate(lr, t, max_steps):
    return lr / (1 + t / (max_steps / 2))


# 计算欧式距离
def euclidean_distance(x, w):
    dis = np.expand_dims(x, axis=(0, 1)) - w
    return np.linalg.norm(dis, axis=-1)


# 特征标准化 (x-mu)/std
def feature_normalization(data):
    mu = np.mean(data, axis=0, keepdims=True)
    sigma = np.std(data, axis=0, keepdims=True)
    return (data - mu) / sigma


# 获取激活节点的位置
def get_winner_index(x, w, dis_fun=euclidean_distance):
    # 计算输入样本和各个节点的距离
    dis = dis_fun(x, w)

    # 找到距离最小的位置
    index = np.where(dis == np.min(dis))
    return (index[0][0], index[1][0])


def weights_PCA(X, Y, data):
    N, D = np.shape(data)
    weights = np.zeros([X, Y, D])

    pc_length, pc = np.linalg.eig(np.cov(np.transpose(data)))
    pc_order = np.argsort(-pc_length)
    for i, c1 in enumerate(np.linspace(-1, 1, X)):
        for j, c2 in enumerate(np.linspace(-1, 1, Y)):
            weights[i, j] = c1 * pc[pc_order[0]] + c2 * pc[pc_order[1]]
    return weights


# 计算量化误差
def get_quantization_error(datas, weights):
    w_x, w_y = zip(*[get_winner_index(d, weights) for d in datas])
    error = datas - weights[w_x, w_y]
    error = np.linalg.norm(error, axis=-1)
    return np.mean(error)


def train_SOM(X,
              Y,
              N_epoch,
              datas,
              init_lr=0.5,
              sigma=0.5,
              dis_fun=euclidean_distance,
              neighborhood_fun=gaussion_neighborhood,
              init_weight_fun=None,
              seed=20):
    # 获取输入特征的维度
    N, D = np.shape(datas)

    # 训练的步数
    N_steps = N_epoch * N

    # 对权重进行初始化
    rng = np.random.RandomState(seed)
    if init_weight_fun is None:
        weights = rng.rand(X, Y, D) * 2 - 1
        weights /= np.linalg.norm(weights, axis=-1, keepdims=True)
    else:
        weights = init_weight_fun(X, Y, datas)

    for n_epoch in range(N_epoch):
        print("Epoch %d" % (n_epoch + 1))
        # 打乱次序
        index = rng.permutation(np.arange(N))
        for n_step, _id in enumerate(index):
            # 取一个样本
            x = datas[_id]

            # 计算learning rate(eta)
            t = N * n_epoch + n_step
            eta = get_learning_rate(init_lr, t, N_steps)

            # 计算样本距离每个顶点的距离,并获得激活点的位置
            winner = get_winner_index(x, weights, dis_fun)

            # 根据激活点的位置计算临近点的权重
            new_sigma = get_learning_rate(sigma, t, N_steps)
            g = neighborhood_fun(X, Y, winner, new_sigma)
            g = g * eta

            # 进行权重的更新
            weights = weights + np.expand_dims(g, -1) * (x - weights)

        # 打印量化误差
        print("quantization_error= %.4f" % (get_quantization_error(datas, weights)))

    return weights


def get_U_Matrix(weights):
    X, Y, D = np.shape(weights)
    um = np.nan * np.zeros((X, Y, 8))  # 8邻域

    ii = [0, -1, -1, -1, 0, 1, 1, 1]
    jj = [-1, -1, 0, 1, 1, 1, 0, -1]

    for x in range(X):
        for y in range(Y):
            w_2 = weights[x, y]

            for k, (i, j) in enumerate(zip(ii, jj)):
                if (x + i >= 0 and x + i < X and y + j >= 0 and y + j < Y):
                    w_1 = weights[x + i, y + j]
                    um[x, y, k] = np.linalg.norm(w_1 - w_2)

    um = np.nansum(um, axis=2)
    return um / um.max()


if __name__ == "__main__":
    # seed 数据展示
    columns = ['area', 'perimeter', 'compactness', 'length_kernel', 'width_kernel',
               'asymmetry_coefficient', 'length_kernel_groove', 'target']
    data = pd.read_csv('seeds_dataset.txt',
                       names=columns,
                       sep='\t+', engine='python')
    labs = data['target'].values
    label_names = {1: 'Kama', 2: 'Rosa', 3: 'Canadian'}
    datas = data[data.columns[:-1]].values
    N, D = np.shape(datas)
    print(N, D)

    # 对训练数据进行正则化处理
    datas = feature_normalization(datas)

    # SOM的训练
    weights = train_SOM(X=9, Y=9, N_epoch=4, datas=datas, sigma=1.5, init_weight_fun=weights_PCA)

    # 获取UMAP
    UM = get_U_Matrix(weights)

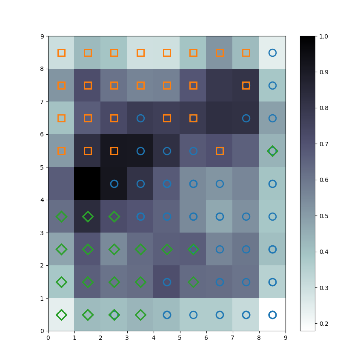
    plt.figure(figsize=(9, 9))
    plt.pcolor(UM.T, cmap='bone_r')  # plotting the distance map as background
    plt.colorbar()

    markers = ['o', 's', 'D']
    colors = ['C0', 'C1', 'C2']

    for i in range(N):
        x = datas[i]
        w = get_winner_index(x, weights)
        i_lab = labs[i] - 1

        plt.plot(w[0] + .5, w[1] + .5, markers[i_lab], markerfacecolor='None',
                 markeredgecolor=colors[i_lab], markersize=12, markeredgewidth=2)

    plt.show()

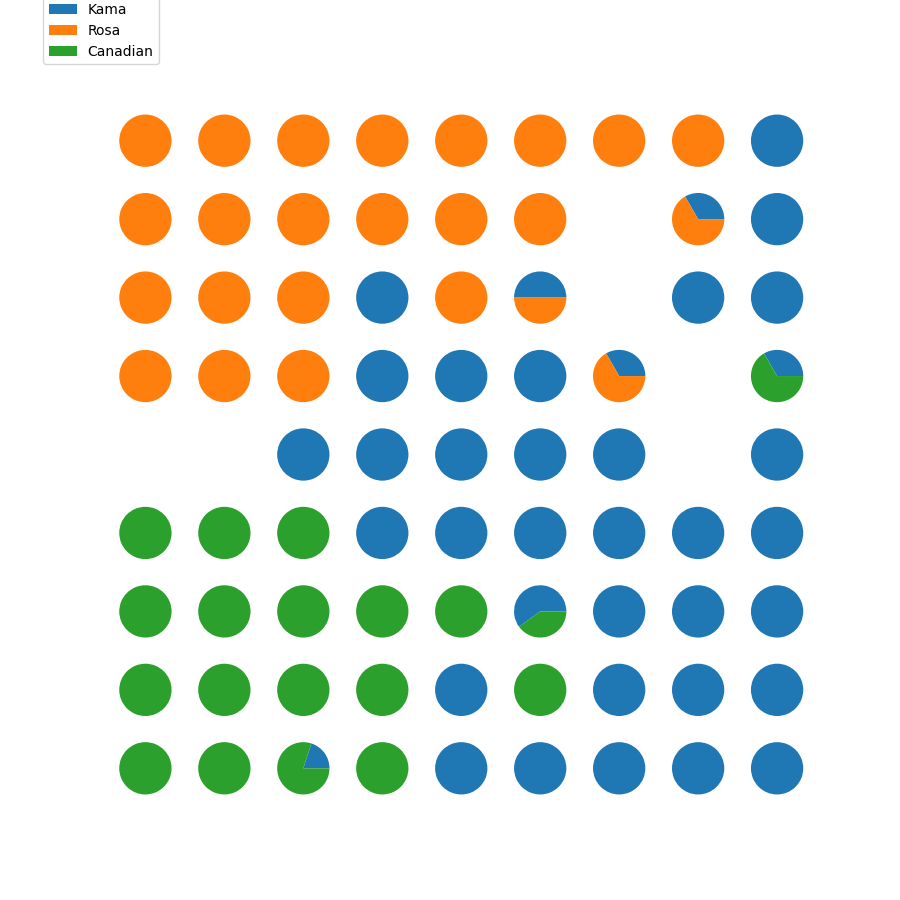
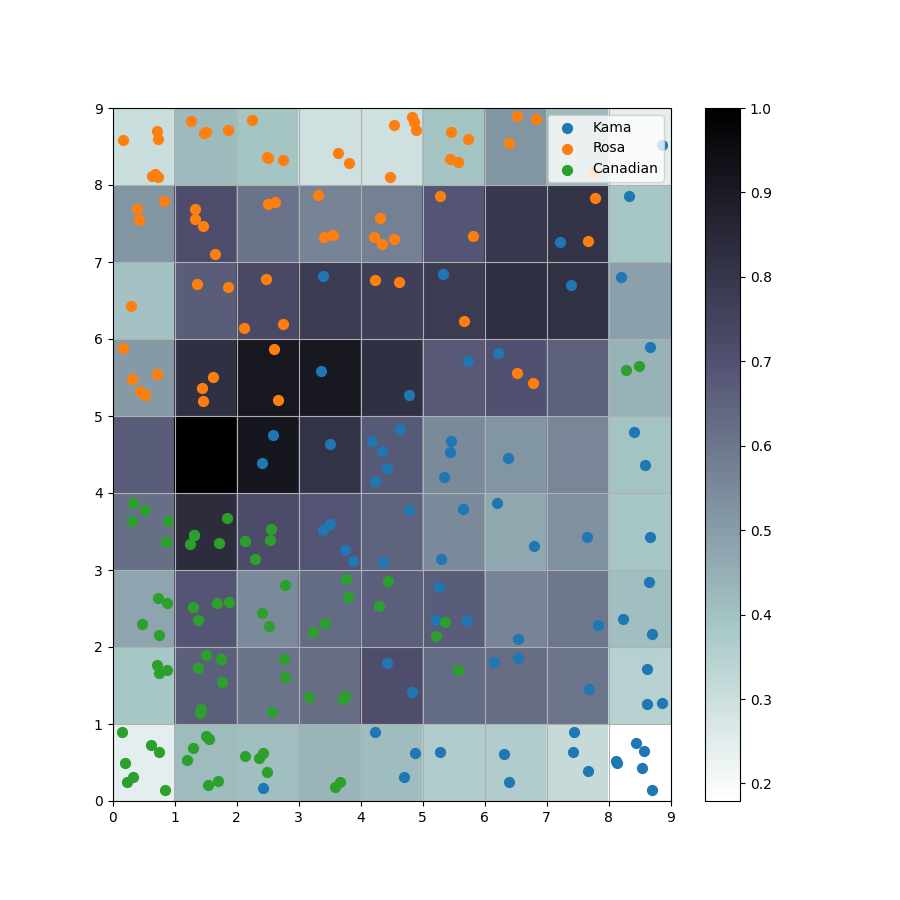
结果图

SOM数据展示

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from SOM import train_SOM, feature_normalization, get_U_Matrix, get_winner_index, weights_PCA
from collections import defaultdict, Counter
import matplotlib.gridspec as gridspec

if __name__ == "__main__":

    # seed 数据展示
    columns = ['area', 'perimeter', 'compactness', 'length_kernel', 'width_kernel',
               'asymmetry_coefficient', 'length_kernel_groove', 'target']
    data = pd.read_csv('seeds_dataset.txt',
                       names=columns,
                       sep='\t+', engine='python')
    labs = data['target'].values
    label_names = {1: 'Kama', 2: 'Rosa', 3: 'Canadian'}
    datas = data[data.columns[:-1]].values
    N, D = np.shape(datas)
    print(N, D)

    # 对训练数据进行正则化处理
    datas = feature_normalization(datas)

    # SOM的训练
    X = 9
    Y = 9
    weights = train_SOM(X=X, Y=Y, N_epoch=4, datas=datas, sigma=1.5, init_weight_fun=weights_PCA)

    # 获取UMAP
    UM = get_U_Matrix(weights)

    print(UM)
    # '''画散点图'''

    # 显示UMAP
    plt.figure(1, figsize=(9, 9))
    plt.pcolor(UM.T, cmap='bone_r')  # plotting the distance map as background
    plt.colorbar()

    markers = ['o', 's', 'D']
    colors = ['C0', 'C1', 'C2']

    # 计算每个样本点投射后的坐标
    w_x, w_y = zip(*[get_winner_index(d, weights) for d in datas])
    w_x = np.array(w_x)
    w_y = np.array(w_y)

    # 分别把每一类的散点在响应的方格内进行打印（+随机位置偏移）
    for c in np.unique(labs):
        idx_target = (labs == c)
        plt.scatter(w_x[idx_target] + .5 + (np.random.rand(np.sum(idx_target)) - .5) * .8,
                    w_y[idx_target] + .5 + (np.random.rand(np.sum(idx_target)) - .5) * .8,
                    s=50, c=colors[c - 1], label=label_names[c])
    plt.legend(loc='upper right')
    plt.grid()
    # plt.show()

    ''' 画饼图'''
    # 计算输出层的每个节点上映射了哪些数据
    win_map = defaultdict(list)
    for x, lab in zip(datas, labs):
        win_map[get_winner_index(x, weights)].append(lab)

    # 统计每个输出节点上，映射了各类数据、各多少个
    for pos in win_map:
        win_map[pos] = Counter(win_map[pos])

    fig = plt.figure(2, figsize=(9, 9))
    # 按照 X,Y对画面进行分格
    the_grid = gridspec.GridSpec(Y, X, fig)
    print(the_grid)

    # 在每个格子里面画饼图
    for pos in win_map.keys():
        label_fracs = [win_map[pos][l] for l in label_names.keys()]

        plt.subplot(the_grid[Y - 1 - pos[1],
                             pos[0]], aspect=1)
        patches, texts = plt.pie(label_fracs)

    plt.legend(labels=label_names.values(), loc='upper left', bbox_to_anchor=(-6, 10))
    # plt.savefig('resulting_images/som_seed_pies.png')
    plt.show()

?结果图